К анализу свойств термопар с позиций механизмов Томсона и контактной термоЭДС

В системах управления теплотехническими объектами для измерения температуры широко используются термоэлектрические термометры, содержащие в своем составе термопару. Термопары являются базовыми элементами термоэлектрических генераторов, используемых напрямую для получения электрической энергии, а также и так называемых термоэлементов, применяемых, например, в холодильной технике и в термоэлектрических тепловых насосах [1, 2]. Термопары используются, кроме того, и в электротепловых преобразователях, применяемых для измерения силы электрического тока.

Актуальность исследуемого вопроса

Согласно [1–4] актуальность теории и практики термоэлектричества для настоящего времени весьма значительна, отмечается недостаточная развитость ряда направлений, а также и большое число публикаций по проблеме [1], в том числе и по истории термоэлектричества [5–7]. Поэтому изучение и выявление всех сторон и особенностей термоэлектрических процессов в термопарах имеет достаточно большое значение, в частности, и с точки зрения учебных целей.

Постановка задачи исследования

Как показал анализ литературных данных, до настоящего времени нет единого общепринятого представления о причинах возникновения термо-ЭДС термопары. Например, в [3, с. 6] отмечается, что «…термоЭДС возникает не в спае, а по длине термоэлектродов», а в [2] по-прежнему считается, что термоЭДС обусловливается контактной разностью потенциалов.

В целом, для объяснения принципа действия термопары привлекают несколько механизмов, чаще всего выделяют два явления:

• 1)    механизм контактной термоЭДС (называемый в литературе эффектом Зеебека);

• 2)    эффект Томсона.

Несмотря на различие данных эффектов, как нам удалось выяснить, формальное описание процессов в термоэлектрических цепях получается совершенно одинаковым. Вместе с тем, насколько нам это известно, в литературе эта тождественность описаний до настоящего времени не была достаточно отчетливо показана[4, 8–15], поэтому есть смысл подробнее остановиться на этом вопросе. При этом подчеркнем, что указанный вопрос является достаточно важным, поскольку, например, в учебной литературе по измерительной технике обычно упоминался механизм контактной термоЭДС [10–15] и поэтому все основные свойства термопар были описаны и обоснованы с позиций этого явления.

Заметим, что значимость эффекта Томсона до сих пор еще подвергается сомнению [1, с. 15, 128], В частности, в [1] на стр. 15 сказано «…эффект Томсона… несомненно присутствует, но не играет определяющей роли», тем не менее, в данной работе мы не будем непосредственно обсуждать этот вопрос.

Отметим также, что возможно именно по причине недостаточной ясности в описании процессов в относительно недавно изданных учебниках по теплотехническим измерениям и приборам [14, 15] это формальное описание просто опущено, в [15, с. 60], например, первое свойство термопар («теорема о третьем проводнике») формулируется «…без доказательства», что вообще-то не является лучшим выходом из создавшегося положения.

Теоретическая часть исследования

Следуя [16], рассмотрим цепь, состоящую из двух разнородных проводников P и Q (рис. 1).

P

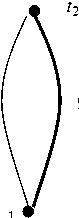
t 1

Рис. 1. Термопара

Как это хорошо известно, в данной цепи контактные термоЭДС образуются в точках 1 и 2 , обозначим их как EPQ(t1) и EQP(t2) . Результирующая контактная ЭДС цепи рис. 1 будет равна Ekz1 = EPQ(tl) + EqP(12) (направление обхода кон- тура против часовой стрелки, порядок чередования индексов соответствует этому направлению), здесь t1 и t2 – температуры контактов. На основании закона Вольта [11, 17] можно записать, что EPQ(t2)+EQP(t2)=0, поэтому Ek21 = EPQ(tl)-EPQ(t2).

Теперь рассмотрим отдельно однородный проводник, пусть, например, это будет проводник Q и пусть его длина равна L . Выделим по длине этого проводника малый участок dx , тогда термоЭДС Томсона, генерируемая на этом участке, будет равна dEg = kg (t) ~dx, где kg (t) — коэффициент

Томсона для проводника Q [9]. Очевидно, термоЭДС Томсона для всего проводника Q дет определяться как

• ^L         dt       ^{t 2}

E g = J k g ⁽ t ⁾7" dx = J k g ⁽ t ) dt = F g ⁽ t )l _t 1 = ₀         dx      _{t 1}

= F g ⁽ t 2 ) ^- F g ⁽ t l ).

Здесь FQ(t) – первообразная для kQ(t) , что бу-

т. е.

dF Q ( t ) dt

= kg (t). Из этого выражения отчетливо видно, что термоЭДС Томсона зависит только от температуры концов проводника Q и не зависит от температуры других его точек. Кроме того, термоЭДС Томсона зависит также и от рода проводника, так как коэффициент Томсона kQ (t) и первообразная для него FQ (t) определяются именно родом проводника Q .

Для проводника P по аналогии можно записать, что E_P = F_P ( t _l) - F_P ( t ₂), здесь контур рис. 1

также обходится против часовой стрелки, поэтому для проводника P начальной точкой будет уже точка 2 . FP (t) – первообразная для коэффициента Томсона проводника P . Таким образом, суммарная термоЭДС цепи рис. 1, обусловленная эффектом Томсона, будет равна et и = Fg(t 2)- Fg(tl)+ fp (tl)- fp (t 2) =

= [ F p ( t l ) - F g ( t l )] - [ F p ( t 2 ) - F g ( t 2 )] =

= fpq (tl) - fpq (t2 ) , где FPg (t) =FP (t) - Fg (t). Отсюда следует, что ET2l, также как и Ek2l, зависит только от рода проводников и температуры их спаев. Причем отметим также, что конечные выражения для Ek2l и ET2l одинаковы с точностью до обозначений.

Как известно, свойства термопар также ранее были описаны и обоснованы с позиций контактной термоЭДС. Поэтому рассмотрим и эти вопросы.

Свойство 1: если в цепь термопары включен третий проводник и его концы находятся при одинаковых температурах, то результирующая термо-ЭДС цепи не изменится.

Рассмотрим первый возможный способ включения третьего проводника (на схеме это проводник R ) в цепь термопары – в разрыв второго контакта проводников P и Q . При таком включении третьего проводника температуры мест его подсоединения должны быть, конечно, равны t ₂ . Для исходной термопары, изображенной на рис. 1, результирующая контактная ЭДС будет равна E_{k 2 l} = E_P g ( t _l) - E_P g ( 1 ₂). Для термопары с третьим проводником (рис. 2) ^E k 2 2 = ^E pg ⁽ t l ) ⁺ E gR ⁽ t 2 ) ⁺ E RP ⁽ t 2 ) .

R

• ^{t 2} P         Q ^t 2

t 1

Рис. 2. Первый способ включения третьего проводника в цепь термопары

Если в цепи с третьим проводником температуры всех контактов будут одинаковы и равны t2 , то на основании закона Вольта можно записать EPg (12) + EgR (12) + ERP (12) = 0 , следовательно EgR (12) + Erp (12) = - EPg (12). Подставляя это соотношение в формулу для суммарной кон- тактной термоЭДС цепи рис. 2 Ek22, получим, что

E k 2 2 = E PQ ⁽ t 1 ) - E PQ ⁽ t 2 ) , т. е. E k 2 2 = E k 2 1 •

Если теперь считать, что в цепи (см. рис. 2) проявляет себя только эффект Томсона, то получим, что суммарная термоЭДС Томсона для цепи рис. 2 будет равна

^E T 2 2 = F Q ⁽ t 2 ) - F Q ⁽ t 1 ) + F R ⁽ t 2 ) - F R ⁽ t 2 ) +

+ F P ( t 1 ) - F P ( t 2 ) = F PQ ( t 1 ) - F PQ ( t 2 ),

• т. е. E T _{2 2} = E T ₂ 1 . При этом заметим, что для получения конечного соотношения не потребовалось привлекать какие-то дополнительные данные, в том числе и закона Вольта.

Далее, рассмотрим второй возможный способ включения третьего проводника в цепь термопары – в разрыв одного из проводников, например, Q (рис. 3).

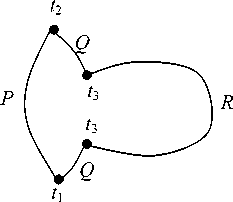
Рис. 3. Второй способ включения третьего проводника в цепь термопары

При таком включении третьего проводника температуры мест его подсоединения должны быть равны между собой, но совсем не обязательно должны быть равны t ₂ . В данном случае результирующая контактная термоЭДС для цепи рис. 3 будет равна

^E k 23 = E PQ ⁽ t 1 ) + E QR ⁽ t 3 ) + E RQ ⁽ t 3 ) + E QP ⁽ t 2 ) , но E rq ( t 3 ) = - E qr ( 1 3 ), поэтому

E k 23 = E PQ ⁽ t 1 ) + E QP ⁽ t 2 ) = E PQ ⁽ t 1 ) ^- E PQ ⁽ t 2 ) , т. е. равна ЭДС исходной цепи.

Если теперь считать, что в цепи рис. 3 также проявляет себя только эффект Томсона, то получим, что суммарная термоЭДС Томсона для цепи рис. 3 будет равна

E T 2 3 = F Q ⁽ t 3 ) - F Q ⁽ t 1 ) ⁺ F R ⁽ t 3 ) - F R ⁽ t 3 ) ⁺

⁺ F Q ⁽ t 2 ) - F Q ⁽ t 3 ) ⁺ F P ⁽ t 1 ) - F P ⁽ t 2 ) =

= F PQ ⁽ t 1 ) ^- F PQ ⁽ t 2 ).

Таким образом, доказательство справедливости свойстватакже получилось заметно проще.

Свойство 2: термоЭДС термопары является функцией только двух температур – температур ее спаев и не зависит от температур других точек термопары. Нетрудно видеть, что данное свойство вполне очевидно с точки зрения вышеизложенного, т. е. как с точки зрения первого, так и второго из рассматриваемых эффектов.

Свойство 3 (сформулируем в формульном виде для эффекта Томсона):

ET2!(t, to) = ET2!(t,to) + ET2!(to,to), т. е. если температуры спаев термопары равны t и 10, то термоЭДС ET21(t, 10), генерируемая при этих температурах, будет равна алгебраической сумме двух термоЭДС, одна из которых генерируется этой же термопарой при температурах t и t0' , а другая – при температурах t0'' и t0 .

Данное свойство используется, как правило, для приведения показаний термопары к градуировочным условиям, т. е. к температуре свободных концов в 0 °С.

Действительно,

E t 21 ( t , t o ) + E t 21 ( t o , t o ) =

''

= F PQ ⁽ t ) - F PQ ⁽ t o ) ⁺ F PQ ⁽ t o ) - F PQ ⁽ t o ) =

= F PQ ⁽ t ) - F PQ ⁽ t o ) = ^E T 21⁽ t , t o ).

Доказательство данного свойства с позиций механизма контактной термоЭДС широко известно и приводится в литературе, например, в [11].

Практическая значимость результатов

В целом, все вышеизложенное, как нам представляется, может служить неким расширенным теоретическим обоснованием широко используемых на практике законов термоэлектрических цепей. К месту заметим, что в [4, с. 12], по-види-мому, из-за отсутствия отчетливого формального описания и обоснования эти законы (правила) названы только «экспериментальными».

Выводы

Рассмотрены вопросы формального (математического) описания процессов генерации термо-ЭДС в термопарах как с позиций механизма контактной термоЭДС, так и с позиций эффекта Томсона. Показано, что конечные соотношения с точностью до обозначений получаются одинаковыми для обоих механизмов. Поэтому достаточно уверенно можно пользоваться теми формулами и свойствами для термоЭДС, которые, насколько это нам известно, исторически первыми были получены и обоснованы для механизма контактной термо-ЭДС. При этом, конечно, следует иметь в виду, что вид этих формул соответствует одновременно и эффекту контактной термоЭДС и эффекту Томсона. Таким образом, свойства термоЭДС термопар абсолютно не различимы с позиций механизма контактной термоЭДС и с позиций эффекта Томсона, т. е., опираясь на данные свойства, нельзя сделать заключение о том, что возникновение термоЭДС в термопаре обуславливается только механизмом контактной термоЭДС или только эффектом Томсона.