К анализу возможности повышения энергетической эффективности генераторных устройств для бортовых радиоэлектронных средств

В условиях освоения космических программ остро встает проблема обеспечения энергоресурсами автономных объектов, предназначенных для длительного пребывания на орбите или в межпланетном пространстве. Одним из путей обеспечения длительной работоспособности космических объектов является повышение энергетической эффективности основных потребителей бортовых электронных систем. В частности, это относится к мощным генераторным устройствам средств радиосвязи.

В мощных радиоустройствах достаточно широко использовался «бигармонический режим» генератора. С появлением мощной твердотельной электроники применение нашли двухтактные схемы последовательных резонансных инверторов (генераторы класса «Д») [1].

Возможность повышения КПД и мощности была обнаружена при работе генератора на расстроенную нагрузку еще в 1960-е гг. Е. П. Хмельницким [2]. Генераторы аналогичного типа в зарубежной литературе получили условное название «генератор класса Е», а в отечественной – «ключевой генератор с формирующим контуром» [3]. Несмотря на то что генераторы класса «Е» обеспечивают высокий КПД на предельных для ключевого режима час- тотах, в силу ряда причин их применение ограничивается пока стадией эксперимента. Цель настоящей работы – провести анализ энергетической эффективности генератора с формирующим контуром в самом общем виде, в широ- ком диапазоне частот и параметров схемы.

Анализ схемы генератора. Упрощенная схема исследуемого генератора представлена на рис. 1.

Полагая, что отпирание и запирание активного элемента (АЭ) полностью определяется управляющим напряжением U _у, представим исследуемый генератор двумя эквивалентными схемами, отражающими процессы в генераторе при открытом и закрытом состоянии АЭ, где u_к = U_к sin ( τ + ϕ ); τ = ω t ; 2 θ – угол, соответствующий времени, в течение которого АЭ находится в открытом состоянии; i_{L 1}, i_L – токи во внешней цепи генератора, для соответствующих эквивалентных схем.

Дифференциальные уравнения для эквивалентных схем принимают вид d2i1di L+L+ν2iL= dτ2 rωC dτ

ν ² E     ν ² sin( τ+ϕ ) cos( τ+ϕ )

u_k ( +

ω L

-

),

r

r

^{diL 1} + ν ² i_{L 1} =- ^{u k} cos( τ +ϕ ).           (2)

d τ ²           ω L

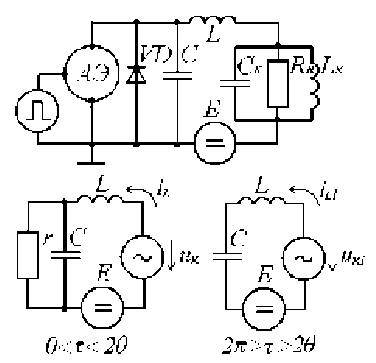
Рис. 1. Схема генератора: АЭ – активный элемент (транзистор, лампа), работающий в режиме «ключа»;

VD – диод, обеспечивающий рекуперацию энергии реактивных элементов при «разомкнутом ключе»;

L , C – элементы контура, определяющие форму напряжения на АЭ; L_к , C_к – нагрузочный контур, настроенный на частоту управляющего напряжения

На основании формул (3)–(6) при условиях (7)–(9) получим

I ₁₁ = A ₁ +ξ ( B ₁₁sin ϕ+ B ₁₂ cos ϕ );

I ₁₂ = A ₂ +ξ ( B ₂₁sin ϕ+ B ₂₂ cos ϕ )

I ₂₁ = A ₃ +ξ ( B ₃₁sin ϕ+ B ₃₂ cos ϕ );

I ₂₂ = A ₄ +ξ ( B ₄₁sin ϕ+ B ₄₂ cos ϕ )

^a 2 ^b 3 ^{- a} 3 ^b 2          ^a 2 ^b 41 ^{- a} 41 ^b 2 B = ^{a 42 b 1 - a 1 b 42} ;

A =             ; B =            ;

ab - ab           a ₁ b ₂ - a ₂ b ₁            a ₁ b ₂ - a ₂ b ₁

где a3b1-a1b3 B12 = a2b42-a42b2; B = a41b1 - a1b41

• A2 =             ; 12 ab- ab 21

• a ₁ b ₂ - a ₂ b ₁            1221            a ₁ b ₂ - a ₂ b ₁

a ₁ = 1 - e ^{2 p 1 θ}⋅ cos2 ν ( π-θ ) - ^{p 1} e ^{2 p 1 θ} sin2 ν ( π-θ );

ν

a2=1-e2p2θ⋅cos2ν(π-θ)-p1e2p2θ⋅sin2ν(π-θ); ν a3 = σ[1-cos2ν(π - θ)];

a ₄₁ =-ε ₂ + q ₁ ⋅ cos2 ν ( π-θ ) + q ₂ ⋅ sin2 ν ( π-θ );

ν

a ₄₂ =ε ₂ - q ₂ ⋅ cos2 ν ( π-θ ) + q ₁ ⋅ sin2 ν ( π-θ ); ν

Решение этих уравнений может быть записано в следующем виде:

i =σ+ξε ₁ cos( τ+ϕ ) -

-ξε ₂sin( τ + ϕ ) + I ₁₁ e ^{p 1 τ} + I ₁₂ e ^{p 2 τ}

...,

i ₁ = I ₂₁ cos ν ( τ - 2 θ ) +

+ I ₂₂ sin ν ( τ- 2 θ ) - ₂ ν ²

-

₁ ξ cos( τ + ϕ ),

U =-ξε ₁sin( τ+ϕ ) -ξε ₂cos × × ( τ+ϕ ) + p ₁ I ₁₁ e ^{p 1 τ}+ p ₂ I ₁₂ e ^{p 2 τ} ,

b1=-p1[1-e2p1θ⋅cos2ν(π-θ)+p2e2p1θ⋅sin2ν(π-θ)]; ν b2=-p2[1-e2p2θ⋅cos2ν(π-θ)+p1e2p2θ⋅sin2ν(π-θ)]; ν p1

b3 =-1 sin2ν(π - θ); ε3=ε1+

3 ν b41=ε2-q1⋅cos2ν(π-θ)+νq2⋅sin2ν(π-θ);

A 3 =σ+ A 1 e ^{2 p 1 θ}+ A 2 e ^{2 p 2 θ} ; A ₄ = ^{p 1} A ₁ e ^{2 p 1 θ} + ^{p 2} A ₂ e ^{2 p 2 θ} ; νν

B ₃₁ = B ₁₁ e ^{2 p 1 θ}+ B ₂₁ e ^{2 p 2 θ}- q ₁; q ₁ = ( ε ₃sin2 θ + ε ₂cos2 θ );

B ₃₂ = B ₁₂ e ^{2 p 1 θ}+ B ₂₂ e ^{2 p 2 θ}- q ₂; q ₂ = ( ε ₃cos2 θ-ε ₂sin2 θ );

B 41 = ¹( p 1 B 11 e ^{2 p 1 θ} + p 2 B 21 e ^{2 p 2 θ} - q 2 );

ν

U ₁ = ν I ₂₂ cos ν ( τ - 2 θ ) -

-ν I ₂₁ sin ν ( τ- 2 θ ) + ¹    ξ sin( τ+ϕ ),

ν ² - 1

ω L где i = i_{L E} ,

ω L       L di_L

= i_{L 1}      , u = ^L , u

^{L 1} E       Ed τ ¹

L di_{L 1}

Ed τ ^;

p ₁ =-      , p ₂ =- – корни характеристического урав-

¹     ω rC       σ

σ

нения    (1);

ν ²

ε ₁

p 1² - ( ν ² - 1)

p 1 + ( ν ² - 1) ^{2 ,}

ε

ω ² LC ^, σν ⁴

ω L σ= , r

U ξ= ^k

E ^,

B 42 = ¹ ( p 1 B 12 e ^{2 p 1 θ} + p 2 B 22 e ^{2 p 2 θ} - q 1 ). ν

Подставляя значения постоянных интегрирования формулы (10) в уравнения (3)–(6), получим описание тока и напряжения на индуктивности в установившемся режиме генератора.

Энергетические показатели генератора. Для определения энергетических показателей генератора необходимо определить ток первой гармоники в нагрузке и ток, потребляемый от источника питания:

²    p 1² + ( ν ² - 1)

₂; I ₁₁; I ₁₂; I ₂₁; I ₂₂

-

^I 1 s ^I 1 c cos ϕ    sin ϕ ^,

постоянные интегрирования.

Полагая режим генератора установившимся, определим постоянные интегрирования, используя принцип непрерывности тока в индуктивности и напряжении на емкости контура LC :

i(0)=i1(2π);i(2θ)=i1(2θ), uc=uc1(2π);uc(2θ)=uc1(2θ),

где

I где tg ϕ= 1c ,

I _{1 s}

₁ 2 θ                    ₁ 2 π

I _{1 s} = i_L sin τ d τ+      i_{L 1}sin τ d τ=

^π 0                ^π 2 θ

_E 2 θ 2 π

= ( ∫ i sin τ d τ+ ∫ i ₁sin τ d τ ) = πω L _02θ

E

= [ A ₅ +ξ ( B ₅₁sin ϕ+ B ₅₂ cos ϕ )]; πϖ L

u = E - u - u . ckL

₁ 2 θ                    ₁ 2 π

I _{1 c} = ∫ i_L cos τ d τ+ ∫ i_{L 1}cos τ d τ= ^π 0                ^π 2 θ                 (13)

E

= [ A ₆ +ξ ( B ₆₁sin ϕ+ B ₆₂cos ϕ )]. πϖ L

При этом параметры A ₅, A ₆, B ₅₁, B ₅₂, B ₆₁, B ₆₂ определяются следующими выражениями:

A ₅ = ¹[ σ (1 - cos2 θ ) + ^{A 1} d ₁₂ + π                  1 + p ₁ ²

+        ( A ₃ d ₁₃ + A ₄ d ₁₄)],

ν ² - 1

11sin4 θ cos4 θ 1

^{B 51 =}ν ² - 1 ⁺ [ ε 3 ( -θ ) +ε 2 ( - ) + ν ² - 1 π 444

+   ^{B 11} d 11 +   ^{B 21}   d 12 + ¹( B 31 d 13 + B 41 d 14 )],

1 + p ₁ ² 1 + p ₂ ² ν ² - 1

1 I η=ξ .

2 /

Поскольку ξ=Uk=I1Rн=I1sRн,то согласно выра-EEcos ϕ жению (12)

ξ=

R_н [ A ₅ +ξ ( B ₅₁sin ϕ+ B ₅₂cos ϕ )] ω L cos ϕ

С другой стороны,

I _{1 c =} A ₆ +ξ ( B ₆₁sin ϕ+ B ₆₂cos ϕ )

I _{1 s}   A ₅ +ξ ( B ₅₁sin ϕ+ B ₅₂cos ϕ )^.

Система трансцендентных уравнений (17), (18) позво- ляет определить искомое значение ξ.

В качестве примера, с помощью ПЭВМ был выполнен расчет КПД генератора для частного случая θ = 90° и

Rн = 5 r .

B 52 = ¹[ ε 2 (^{sin4 θ} π 4

-

θ ) -ε 3 (^cos₄^{4 θ}

-

¹₄) +

BB + ¹¹ d + ²² 1 + p 1²¹¹ 1 + p 2²

1 d ₁₂ + ₂

-

₁( B ₃₂ d ₁₃ + B ₄₂ d ₁₄)],

где d ₁₁ = 1 - e ^{2 p 1 θ} (cos2 θ- p ₁ sin2 θ ); d ₁₂ = 1 - e ^{2 p 2θ} (cos2 θ- p ₂sin2 θ ); d ₁₃ = cos2 ν ( π-θ ) - cos2 θ ; d ₁₄ = sin2 ν ( π-θ ) +ν sin2 θ ;

1 A

A ₆ = [ σ sin2 θ+ ¹ d ₂₁ +

π             1 + p ₁ ²

₊ A 2 1 + p ₂ ²

1 d ₂₂ + ₂

-

₁( A 3 d 23 + A 4 d 24 )],

B 61 = ¹[ ε 3 ( π

cos 4 θ 4

-

Зависимость КПД генератора от частоты и параметров LC контура на плоскости переменных р ₁, р ₂ приведена на рис. 2.

+ ^{B 11} d 1 + p 1²²¹

B62=-ν2-

+

^B 21

₂ d ₂₂

1 + p ₂

1      sin4 θ

₄) -ε 2 (₄ +θ ) +

( B ₃₁ d ₂₃ + B ₄₁ d ₂₄)], ν ² - 1

1sin4 θ cos4 θ + [ ε ₂( +θ ) +ε ₃(

1 π 44

-

14)+

+ ^{B 12} d + ^{B 22} 1 + p 1²²¹ 1 + p 2²

1 d ₂₂ + ₂

-

₁( B ₃₂ d ₂₃ + B ₄₂ d ₂₄)],

где d ₂₁ =- p ₁ + e ^{2 p 1 θ} ( p ₁cos2 θ+ sin2 θ );

d ₂₂ =- p ₂ + e ^{2 p 2 θ} ( p ₂cos2 θ+ sin2 θ ); d 23 =ν sin2 ν ( π-θ ) + sin2 θ ;

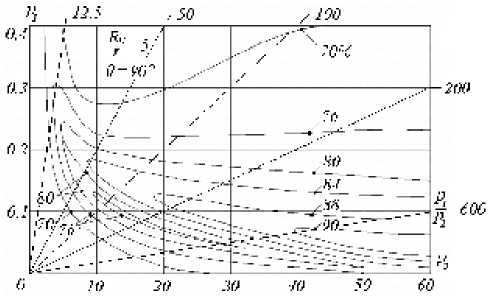
Рис. 2. КПД генератора

В перв ом

ω p ₁ p ₂ = ⁰ ; ω 0 ω

приближении 1

r

p 1 ^≈ω rC ^; p 2 ω L

;

LC

.

Частотные характеристики КПД генератора можно получить построением поверхности (рис. 2) плоскостями,

соответствующими конкретным значениям отношения

d ₂₄ = cos2 θ- cos2 ν ( π - θ ).

Ток, потребляемый от источника, определяется как

2 θ 2 θ

I 0 = ^{1 Uc} d τ= ^{1 E - Uk}

2 π ₀ r 2 π ₀ r

-

^UL d τ=

E2θ a    σ[1-ξsin(τ+ϕ)-u]dτ,

2 πω L ₀

где u определено выражением (5).

Результат интегрирования в выражение (14) следующий:

Eσ

I ₀ = ^a   {2 θ+ξ [cos(2 θ+ϕ ) - cos ϕ ](1 -ε ₁) +

2 πϖ L

+ ξε ₂[sin(2 θ + ϕ ) - sin ϕ ] +              ⁽¹⁵⁾

+ I 11 (1 - e ^{2 p 1 θ} ) + I 12 (1 - e ^{2 p 2 θ} )}.

Коэффициент полезного действия на первой гармонике определяется известным соотношением [3]:

p2; графики КПД в функции от   =ω представлены p1                                   p2    r на рис. 3, где также рассмотрен частный случай θ = 900 и

Rн = 5 r .

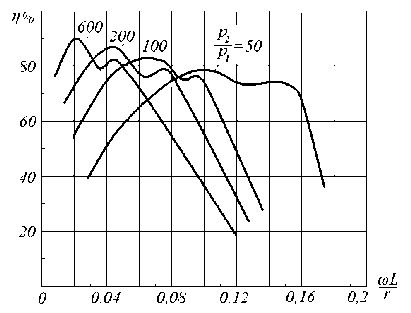
Рис. 3. Частотные характеристики генератора

Из проведенного анализа следует, что непосредственные расчеты энергетических показателей генератора весьма трудоемки из-за громоздких выкладок и невозможности аналитического решения системы уравнений (17), (18).

Поэтому в каждом конкретном случае целесообразно прибегнуть к численным методам с использованием вычислительной техники.

На основании приведенного примера можно сделать вывод о возможности значительного повышения электронного КПД генератора по сравнению с обычными усилителями мощности, КПД которых на высоких частотах не превышает 40–60 %.