К апостериорному моделированию нестационарных гиперболических систем

К апостериорному моделированию нестационарных гиперболических систем

Автор: Данеев Алексей Васильевич, Русанов Вячеслав Анатольевич, Русанов Марк Вячеславович, Сизых Виктор Николаевич

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Рубрика: Информатика, вычислительная техника и управление

Статья в выпуске: 1-1 т.20, 2018 года.

Бесплатный доступ

В контексте качественной теории дифференциальной реализации бесконечномерных управляемых динамических систем приводятся результаты исследований тополого-алгебраических свойств семейств непрерывных динамических процессов (отображений «вход-выход») в проблеме разрешимости задачи реализации этих семейств в классе обыкновенных нестационарных дифференциальных уравнений второго порядка (в том числе гиперболических) в сепарабельном гильбертовом пространстве. Попутно обосновываются аналитико-геометрические условия непрерывности проективизации нелинейного оператора Релея-Ритца с вычислением фундаментальной группы его образа.

Дифференциальная реализация, нестационарная гиперболическая модель, олд / рлд-совместимость

Короткий адрес: https://sciup.org/148205406

IDR: 148205406

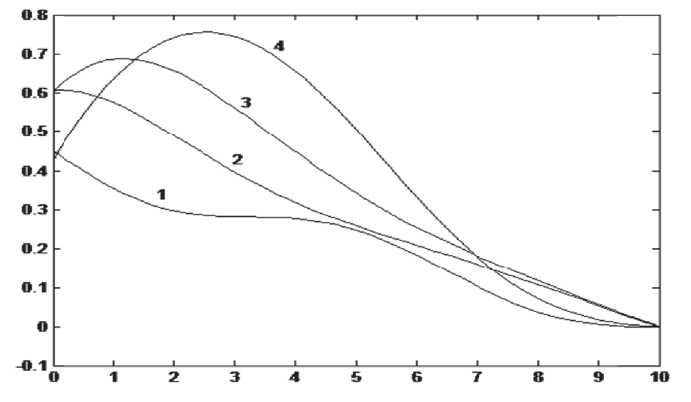
Список литературы К апостериорному моделированию нестационарных гиперболических систем

  • Ahmed N.U. Optimization and Identification of Systems Governed by Evolution Equations on Banach Space. New York: John Wiley and Sons, 1988.
  • Сергиенко И.В., Дейнека В.С. Идентификация параметров эллиптико-псевдопараболических распределенных систем//Кибернетика и системный анализ. 2011. № 4. С. 28-50.
  • Аниконов Ю.Е., Нещадим М.В. Об аналитических методах в теории обратных задач для гиперболических уравнений//Сиб. журн. индустр. математики. 2011. Т. 14, № 1. С. 27-39; № 2. С. 28-33.
  • Виллемс Я. От временного ряда к линейной системе//Теория систем. Математические методы и моделирование . М.: Мир, 1989. С. 8-191.
  • Данеев А.В., Русанов В.А., Шарпинский Д.Ю. Нестационарная реализация Калмана-Месаровича в конструкциях оператора Релея-Ритца//Кибернетика и системный анализ. 2007. № 1. С. 82-90.
  • Daneev A.V., Lakeev A.V., Rusanov V.A., Rusanov M.V. On the Theory of Realization of Strong Differential Models//Journal of Applied and Industrial Mathematics. 2007. Vol. 1, № 3. P. 273-282.
  • Rusanov V.A., Antonova L.V., Daneev A.V. Inverse Problem of Nonlinear Systems Analysis: A Behavioral Approach//Advances in Differential Equations and Control Processes. 2012. Vol. 10, № 2. P. 69-88.
  • Русанов В.А., Лакеев А.В., Линке Ю.Э. Существование дифференциальной реализации динамической системы в банаховом пространстве в конструкциях расширений до Мр-операторов//Дифференциальные уравнения. 2013. Т. 49, № 3. С. 358-370.
  • Chen Y.A. New One-Parameter Inhomogeneous Differential Realization of the spl(2,1) Superalgebra//International Journal of Theoretical Physics. 2012. Vol. 51, № 12. P. 3763-3768.
  • Rusanov V.A., Daneev A.V., Lakeev A.V., Linke Yu.É. On the Differential Realization Theory of Nonlinear Dynamic Processes in Hilbert Space//Far East Journal of Mathematical Sciences. 2015. Vol. 97, № 4. P. 495-532.
  • Данеев А.В., Русанов В.А., Русанов М.В. От реализации Калмана-Месаровича к линейной модели нормально-гиперболического типа//Кибернетика и системный анализ. 2005. № 6. С. 137-157.
  • Rusanov V.A., Daneev A.V., Lakeev A.V., Linke Yu.É. A Finite Character Geometrical Property of the Differential Realization of a Set of Dynamic Processes in a Hilbert Space//Advances in Differential Equations and Control Processes. 2014. Vol. 13, № 1. P. 37-45.
  • Русанов В.А., Данеев А.В., Линке Ю.Э. К геометрическим основам дифференциальной реализации динамических процессов в гильбертовом пространстве//Кибернетика и системный анализ. 2017. Т.53, №4. С. 71-83.
  • Рид М., Саймон Б. Методы современной математической физики. Том 1. Функциональный анализ. М.: Мир, 1977.
  • Кириллов А.А. Элементы теории представлений. М.: Наука, 1978.
  • Kōmura Y. Nonlinear Semi-Groups in Hilbert Space//J. Math. Soc. Japan. 1967. Vol. 19, № 4. P. 493-507.
  • Энгелькинг Р. Общая топология. М.: Мир, 1986.
  • Канторович Л.В., Акилов Г.П. Функциональный анализ. М.: Наука, 1977.
  • Русанов В.А. Об одной алгебре множеств динамических процессов, обладающей дифференциальной реализаций в гильбертовом пространстве//Доклады РАН. 2010. Т. 433, № 6. C. 750-752.
  • Прасолов В.В. Элементы комбинаторной и дифференциальной топологии. М.: МЦНМО, 2014.
  • Понтрягин Л.С. Непрерывные группы. М.: Наука, 1973.
  • Alexandroff P.S. Über stetige Abbildungen kompakter Räume//Math. Ann. 1927. Vol. 96. P. 555-571.
  • Коэн П. Дж. Теория множеств и континуум-гипотеза. М.: Мир, 1969.
  • Rusanov V.A., Daneev A.V., Lakeyev A.V., Linke Yu.É. On Solvability of the Identification-Inverse Problem for Operator-Functions of a Nonlinear Regulator of a Nonstationary Hyperbolic System//Advances in Differential Equations and Control Processes. 2015. Vol. 16, № 2. P. 71-84.
  • Русанов В.А., Шарпинский Д.Ю. К теории структурной идентификации нелинейных многомерных систем//Прикладная математика и механика. 2010. Т. 74, вып. 1. С. 119-132.
  • Лакеев А.В., Линке Ю.Э., Русанов В.А. К структурной идентификации нелинейного регулятора нестационарной гиперболической системы//Доклады РАН. 2016. Т. 468, № 2. C. 143-148.
  • Ван дер Шафт А. К теории реализации нелинейных систем, описываемых дифференциальными уравнениями высшего порядка//Теория систем. Математические методы и моделирование. Сборник статей (ред. А.Н. Колмогоров, С.П. Новиков): Пер. с англ. М.: Мир, 1989. С. 192-237.
  • Юрко В.А. Восстановление дифференциальных операторов переменных порядков на звездообразном графе по спектрам//Дифференциальные уравнения. 2013. T. 49, № 12. С. 1537-1548.
  • Русанов В.А., Лакеев А.В., Линке Ю.Э. К разрешимости дифференциальной реализации минимального динамического порядка семейства нелинейных процессов «вход-выход» в гильбертовом пространстве//Дифференциальные уравнения. 2015. T. 51, № 4. С. 524-537.
  • Whitehead A.N. Science and Modern Word. London: Cambridge University Press, 1953.
  • Эйнштейн А., Инфельд Л. Эволюция физики. Развитие идей от первоначальных понятий до теории относительности и квантов. М.: Молодая гвардия, 1966.
  • Willems J.C. System Theoretic Models for the Analysis of Physical Systems//Ric. Aut. 1979. №.10. P. 71-106.
Еще
Статья научная
QR-код для установки приложения SciUp Наведите камеру и скачайте бесплатное приложение SciUp