К нахождению J-интеграла для трещиноподобного дефекта твердого тела в виде физического разреза в конечно-элементном представлении

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

Исследование прочностных характеристик твердых тел связано с соответствующей моделью разрушения и анализом напряженно-деформированного состояния (НДС). Как правило, процесс разрушения связан с зарождением и ростом трещиноподобных дефектов. В этом случае одним из основным модельных представлений рассматриваемых дефектов является математический разрез. Математический разрез в упругом теле связан с сингулярностью поля напряжений в вершине трещины и в случае линейно упругой среды приводит к асимптотическим решениям [1; 2], связанными с коэффициентами интенсивности напряжений (КИН) [3; 4]. Предельные значения КИН формируют силовой критерий разрушения [5] и энергетический критерий [6; 7], который может быть ассоциирован с инвариантным контурным интегралом ( J -интегралом) [8–10], связывающим берега математического разреза, свободные от внешней нагрузки. Нахождение предельных характеристик трещиностойко-сти, связанных с соответствующим модельным представлением, для однородных [11–13] и композиционных материалов [14–17] определяют подходы экспериментальной механики разрушения [18]. Для нахождения КИН применяют аналитические и численные методы расчета [19–22].

Одним из подходов к нахождению НДС в настоящее время является метод конечных элементов (МКЭ) [23;

24]. В этом случае процессу разрушения может быть сопоставлено последовательное удаление конечных элементов [25; 26], формирующее трещиноподобный дефект, который может быть рассмотрен в качестве физического разреза с характерной толщиной δ0 . В силу того что МКЭ основан на вариационной и, следуя терминологии [27], «ослабленной» постановке задачи, соответствующее решение может приводить к появлению векторов напряжений на свободных поверхностях. Данное обстоятельство имеет место в окрестностях концентраторов напряжений, к которым можно отнести и угловые точки физического разреза.

Формирование энергетической характеристики

Рассматривается нагружение упругого тела с дефектом в виде физического разреза толщиной δ₀ внешней нагрузкой q , приводящей к равновесию тела. Для определения НДС предполагается использование МКЭ. Отметим, что, несмотря на наличие сингулярных точек в тупиковой области физического разреза, конечно-элементное решение задачи для фиксированного разбиения будет приводить к регулярному распределению НДС в окрестности физического разреза. На рис. 1 показана окрестность физического разреза, где точки B и B ’ являются концентраторами напряжений.

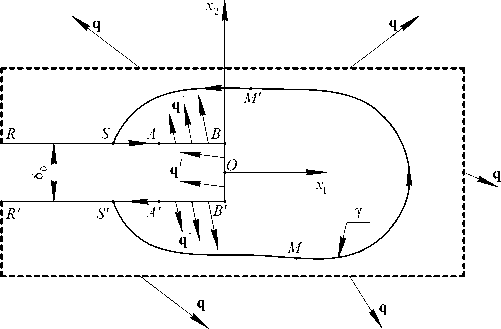
Рис. 1. Физический разрез в упругом теле

Fig. 1. Physical section in an elastic body

J i = J I n 1 V ^- q •

xB

=0,5 J xA

γ2

. ^d u 2

²² d x 1

^x A ' (     d u₂

+ 0,5 1 ^ 22 ² d x, ^x B '                ¹

- 8₀v + 0,5 j I c

- 80/2 v

S u |, 3- I ^d Y 2 = ^{d X} 1 J

d u,

12     1

d x ₁

d u,

12     1

d x ₁

dx1 + x2 =8g/2

dx1 - x 2 =-8o/2

д щ     du,

' 12 a + °11 2

d x ₁        d x ₁

dx ₂,

X i = 0

1 δ0 2

где v = — j" v| ₀ dx₂ - средняя по торцу удельная сво-

80 -4/2

Условие свободной поверхности для узловых точек физического разреза и его торцевой части в рамках конечно-элементной постановки задачи задастся равенством нулю узловых сил, что приводит к наличию векторов напряжений, получаемых в рамках конечно-элементного решения в окрестности физического разреза. Обозначим векторы напряжений, получаемых на частях границ физического разреза в результате решения: q ⁺ =- c₁₂ e ₁ - c₂₂ e ₂ (на AB ), q ^- = c₁₂ e ₁ + o₂₂ e ₂ (на A ’ B ’), где σ _ij – компонента тензора напряжений; i , j = 1, 2; e _i – вектор ортонормированного базиса. На торце физического разреза вектор напряжений будет равен: q l = - c₁₁ e ₁ - c₁₂ e ₂. Полагаем, что на границах RA и R ’ A ’ векторы напряжений нулевые и соответствуют условиям свободной поверхности.

Запишем термомеханическое соотношение [8]:

nV - q ^Y-^ u | d Y = 0,             (1)

O x ^x 1 J

бодная энергия.

С учетом последнего выражения из (2) приходим к представлению:

"B (

J = 8₀v - 0,5 j c₂₂ xA V

^x A ' /

- ^0,5 J I ^c ₂₂

^xB' ^v

$1

Y ^V

где ψ – удельная (к единице объема) свободная энергия;

n ₁ – проекция вектора нормали к поверхности контура на направление оси x ₁ ; γ – замкнутый контур B ’ A ’ S ’ MM ’ SABB ’, показанный на рис. 1, проходящий по свободной поверхности SA и A ’ S ’; q ^γ – распределенная по контуру нагрузка; u – поле перемещений на контуре.

Представим (1) в виде суммы двух контурных интегралов:

J + J 1 = 0,                     (2)

где J = J ^w- q -dU d Y i ; J 1 = J ^ ^у - q • d U^ ; Y 1 —

контур S ’ MM ’ S ; γ₂ – контур SABB ’ A ’ S ’.

Рассмотрим нахождение первого слагаемого в (2) посредством определения интеграла J 1 в рамках модели линейно упругой среды:

d u₂

—² + c d x ₁

d u₂

—² + c

^{d x} 1

d u ₁ d x ₁

dx ₁

^x 2 = ⁸0/²

-

d u ₁

^{d x} 1

dx ₁

^x 2 =^{- 8}c/²

-

80/2 Л

^{- 0,5} J I ^c ₁₂

- 80/2 ^v

d u ₂       d u₁

--+ c 11 — d x ₁        d x ₁

dx ₂.

x 1 = 0

Отметим, что если граничные напряжения на торце и границах удовлетворяют условию свободной поверхности, то из (3) приходим к выражению J = 8₀V , полу-

ченному в [28].

^{Использ} уя связь: V = 0,5 1 а_1Л1 + a₂₂e₂₂+ c ₂| ^d u 2 + ^ 1

V                     V d x ₁ d x ₂

из представления (3) приходим к выражению:

80/2 (

J = 0,5 I I c₂₂e₂₂ + c₁₂

- 80/2 ^V

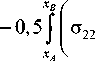
d u

^{2 + C}12^£11 d x ₁

^x A '

-0,5 J xB'

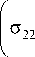
d u ₂

⁺ 0 12 ^ 11 d x ₁

,

d u ₁

d x ₂

dx ₂

x 1 = 0

dx ₁

^x 2 = ⁸c/²

-

-

dx ₁ .

^x 2 =^{- 8}g/²

При стремлении 8₀ ^ 0 физический разрез переходит в математический. При этом трещиноподобный дефект может быть рассмотрен в виде трещины Гриффитса [6]. В этом случае при отсутствии нагрузки на берегах разреза значение J в (2) является J -интегралом Черепанова – Райса [8; 9], значение которого может быть вычислено посредством КИН. Рассмотрим вычисление (4) в рамках МКЭ в программном комплексе ANSYS [29] и модели с тонким слоем на продолжении физического разреза [30] при нагружении трещиноподобного дефекта по моде I и II.

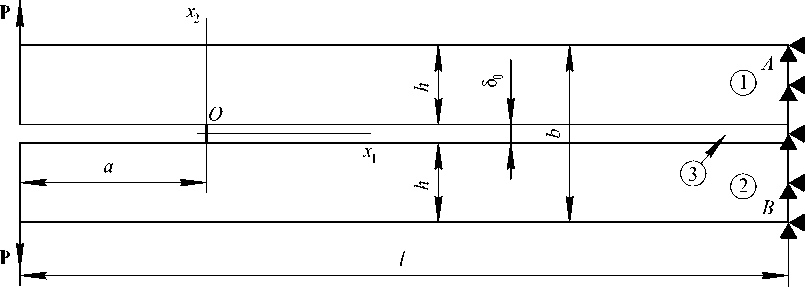
Рис. 2. Модель ДКБ-образца

Fig. 2. Model of the specimens of the double hammer beam

При этом исследуем влияние второго и третьего слагаемого в правой части (4) для различных длин участков интегрирования.

Постановка задач нагружения трещиноподобного дефекта

Рассматриваются задачи в линейно упругой постановке в состоянии плоской деформации. На рис. 2 представлена схема нагружения трещины нормальным разрывом в виде двойной консольной балки (ДКБ) со следующими геометрическими характеристиками: длина образца l = 0,2 м, длина трещины a = 0,05 м, ширина ДКБ-образца b = 0,1 м, ширина консоли h = ( b - 8₀ ) /2 , где δ₀ – варьируемая толщина физического разреза. Тела 1 и 2 соединены адгезионным слоем 3 и имеют следующие механические характеристики: E = 2∙10¹¹ Па, коэффициент Пуассона v = 0,3. При решении задачи рассматривались два случая: случай № 1 – адгезионный слой 3 имеет аналогичные телам 1 и 2 механические свойства (однородное тело с вырезом в виде физического разреза); случай № 2 – адгезионный слой 3 имеет следующие характеристики: модуль упругости E adh = 2∙10⁹ Па, коэффициент Пуассона v _adh = 0,3 (слоистый композит). На консоли ДКБ-образца действуют внешние распределенные нагрузки P = 10³ Па, торец AB жестко закреплен от перемещений, верхние и нижние границы слоя имеют равные перемещения с сопрягаемыми границами тел 1 и 2 (жесткое сцепление).

На рис. 3 представлена схема нагружения трещины поперечным сдвигом в виде образца с двойной выемкой, со следующими геометрическими характеристиками: длина образца l = 0,1 м, длина трещины a = 0,038 м, длина связки 2t = 0,024 м, ширина образца b = 0,13 м, ширина консоли h = (b - 80)/2, где 80 - варьируемая толщина физического разреза. Тела 1 и 2 жестко сцеплены адгезионным слоем 3 и имеют следующие механические характеристики: E = 2^1011 Па, коэффициент Пуассона v = 0,3 . Аналогично ДКБ-образцу, см. рис. 2, рассматриваются два варианта задания механических свойств адгезионному слою 3: № 1 – адгезионный слой 3 имеет аналогичные телам 1 и 2 механические свойства (однородное тело); № 2 – для адгезионного слоя 3 были выбраны следующие механические свойства: модуль упругости Eadh = 2409, коэффициент Пуассона v adh = 0,3 (слоистый композит). На консоли образца с двойной выемкой действуют внешние распределенные нагрузки P = 103 Па, торец образца AB жестко закреплен от перемещений.

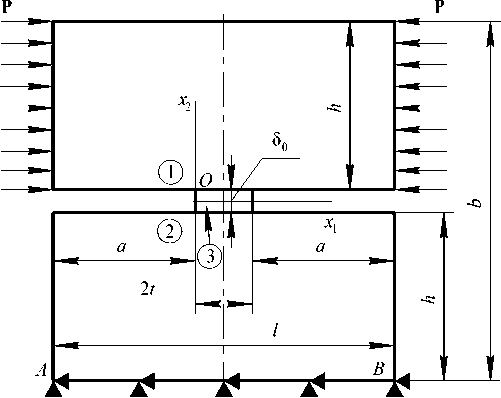
Рис. 3. Модель образца с двойной выемкой

Fig. 3. Model of the double edge notched compression specimens

Результаты расчетов

Рассматривая трещиноподобный дефект в виде математического разреза, с помощью комплекса ANSYS вычислены значения КИН моды нагружения I и II. Результаты расчетов приведены в табл. 1.

J -интеграл для плоской задачи связан с КИН следующим соотношением [11; 13]:

Jk = a K²_k /Е ,                  (5)

где а = 1 для плоского напряженного состояния; а = 1 - V 2 для плоского деформированного состояния; E -модуль упругости; V - коэффициент Пуассона; k = I, II.

Таблица 1

Результаты расчета КИН в ANSYS

J о • - 8е ds + 1 0 22 8 u + dx 1 +

^S 1                    ^l

| о₁₂8 u + dx 1 + l

I      Э ⁸ u +              ^{д 8}и ⁺ , |

+ 0,58 0    о 11----- dx 1 + о₁₂----- dx 1 = P • 8u dl ,

U     dx1       i     dx1     ) L и для тела 2:

j о • - 8s ds - J 0 22 8 и 2 dx 1 - J"

^S 2                  ^l

o₁₂8 u 1 dx 1 +

l

Table 1

Results of calculations of stress intensity factors in ANSYS

Искомая величина	Значение (Н/м3/2)
K I	1295,7
K II	46,7

I      Э ⁸ и               ^{d 8}u₂ , I

+ 0,58₀   o 11----- dx 1 + I o₁₂----- dx 1 \ = P • 8u dl ,

[i       d x 1           i       d x 1       I L

При дальнейшем изложении, без ограничения общности, ограничимся случаем плоской деформации. Из (5) находим эталонное численное значение J -интеграла для математического разреза. Результаты расчета приведены в табл. 2.

Пусть в линейно упругом конечно-элементном решении окончание трещины формирует грань прямоугольного конечного элемента 8 0 х 8 1 с квадратичными функциями формы. На рис. 4 показано окончание физического разреза.

Таблица 2

Результаты расчета J -интеграла

Calculation results of J -integral

Table 2

Искомая величина	Значение (Н/м)
J I	7,639∙10-6
J II	9,923∙10-9

где S_i – площади тел; L_i – контуры приложения внешней нагрузки P в телах; σ , ε – тензоры напряжений и деформаций в телах; u – вектор перемещений; ∙ – скалярное умножение; ∙∙ – двойное скалярное умножение; σ₁₁,σ₂₂,σ₁₂ , ε₁₁, ε₂₂, ε₁₂ – компоненты тензоров средних напряжений и деформаций слоя с соответствующими компонентами:

1 0,5δ0

О 21 = 0 12 =7“ J 0 21 ( x 1 , x 2 ) dx 2 ,

⁸0 - O,58o

1 0,5δ0

o₂₂ = o₂₂ ( x 1 , x 2 ) dx 2 ,

⁸⁰ - O,58o

1 0,5δ0

^o11 = J ^o11 ( ^x 1 , ^x 2 ) ^dx 2 ,

⁸⁰ - 0,580

^e22 =

( x ) - u 2 ( x )

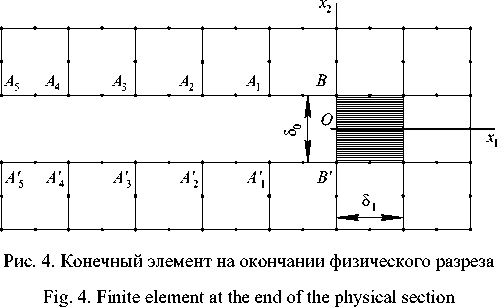
^e21 = ^ 12 = ^0,5

e_n = 0,5

Э u+ (x1) 4   dx1

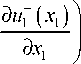
^{1 u} + ( x 1 ) - u 1 ^-( x 1 ) _{+ 0} 5 1 ^d u ⁺ ( x 1 ) ₊ ^d u - ( x 1 ) T ,         ⁸0             , [ ^d x 1         ^d x 1 i

_   +   -    ___________    _   _ _ _    _ _                      _ где ui , ui - соответственно компоненты векторов пере-

мещений верхней и нижней границ слоя. Определяющие

соотношения в слое рассматриваются относительно средних характеристик НДС.

В случае рассмотрения модели слоя взаимодействия первое слагаемое в (4) преобразуется к виду

При конечно-элементной аппроксимации геометрии будем требовать выполнения следующего условия: 8 1 = 8 0 . Исходными данными для вычисления (4) будут найденные в ANSYS и на основе модели слоя взаимодействия [30] поля перемещений при их локальной квадратичной аппроксимации на рассматриваемых конечных элементах.

В случае модели слоя взаимодействия равновесие связанных тонким слоем двух тел рассматривается в рамках системы вариационных уравнений [30] для тела 1:

0, 5 o 22 ^ 22

. Для нагружения слоя по

моде I имеет место: o₁₂ = 0 , а для нагружения по моде II: o₂₂ = 0. Для решения в комплексе ANSYS первое слагаемое в (4) интегрируется по найденному на торце элементу слоя НДС. Второе и третье слагаемые в рассматриваемых подходах определяются интегрированием по найденному НДС на границах физического разреза.

Для нагружения ДКБ-образца с математическим разрезом по моде I рассмотрим выражение для КИН K _I ^a [31; 32]:

K a = 12 ( Ph ) ² /h ( a/h ) ² [ 1 + 0,673 ( h/a ) ] 2 .     (6)

Согласно работе [33] линейно упругое аналитическое решение для образца с двойной выемкой, геометрические параметры которого конечны и удовлетворяют условию t <  h/п , остается справедливым, и соотношение для КИН K _I ^a _I принимает следующий вид:

K a = P/ 4 vn t .                 (7)

Результаты вычисления (6), (7) и их погрешность относительно решения ANSYS приведены в табл. 3.

Таблица 3

Результаты расчета КИН

Table 3

Calculation results of stress intensity factors

Искомая величина	Значение (Н/м3/2)	Погрешность, %
K I a	1295,9	0,02
K I a I	48,5	3,85

На рис. 5 приведены зависимости относительной величины J k = J/J k по представлению (4), для варианта задания механических свойств №1, от десятичного логарифма относительной величины физического разреза 5 ₀ = 5 ₀ / h при приложении нагрузки P . Графики 1 и 2 соответствуют определению НДС при решении в ANSYS для нагружений по моде I и II соответственно, графики 3 и 4 – МКЭ-решению на основе модели слоя взаимодействия [30] для нагружений по моде I и II соответственно.

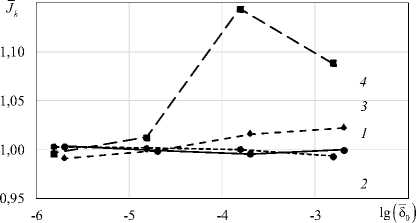
Рис. 5. Зависимости относительных значений J -интегралов от относительной величины физического разреза

• Fig. 5.    Dependences of the relative J -integrals on the relative magnitude of the physical section

Из рис. 5 следует, что при относительно небольшой толщине физического разреза наблюдается хорошая сходимость J -интеграла, полученного по представлению (4) для решения ANSYS и МКЭ-решения на основе модели [30] к значениям J -интеграла для математического разреза при решении ANSYS.

На рис. 6 показаны относительные значения компонент J _I представления (4) для варианта задания механических свойств №1 при решении в ANSYS (гистограммы с непрерывным контуром) и МКЭ-решении на основе модели [30] (гистограммы с пунктирным контуром) к решению ANSYS для трещины в виде математического разреза, см. табл. 2, от относительной величины физического разреза δ ₀ для нагружения по моде I.

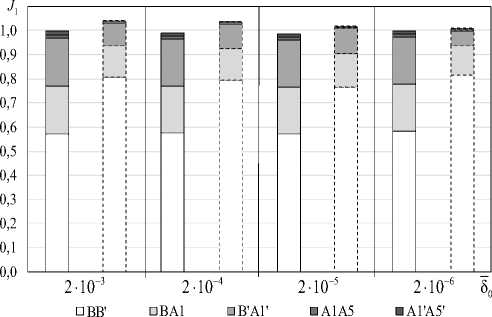
Рис. 6. Зависимости относительных значений составляющих J-интегралов,   полученных по представлению (4), от относительной величины физического разреза

• Fig. 6.    Dependences of the relative values of the components of the J -integrals obtained according to representation (4) on the relative magnitude of the physical section

На рис. 7 показаны относительные значения компонент J _II представления (4) для варианта задания механических свойств №1 при решении в ANSYS (гистограммы с непрерывным контуром) и МКЭ-решении на основе модели [30] (гистограммы с пунктирным контуром) к решению ANSYS для трещины в виде математического разреза, см. табл. 2, от относительной величины физического разреза δ ₀ для нагружения по моде II.

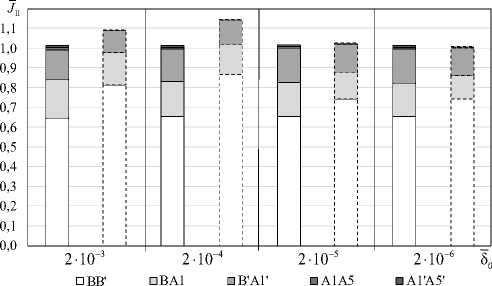
Рис. 7. Зависимости относительных значений составляющих J-интегралов,   полученных по представлению (4), от относительной величины физического разреза

• Fig. 7.    Dependences of the relative values of the components of the J -integrals obtained according to representation (4) on the relative magnitude of the physical section

Из рис. 6, 7 видно, что для физического разреза в материале с однородными механическими характеристиками аддитивные слагаемые имеют одинаковый порядок величины при большем значении на торцевой части. Погрешность вычисления первого слагаемого представления (4) для изотропного тела при 5 0 = 2 - 10 - 6 между решениями по ANSYS и МКЭ на основе модели [30] составляет: 28 % при нагружении по моде I; 12 % по моде II.

Результаты вычисления относительного значения компонент J -интеграла представления (4) для слоистого композита при решении в ANSYS к решению ANSYS для трещины в виде математического разреза, см. табл. 2, от относительной толщины адгезионного слоя δ ₀ при нагружении по моде I приведены в табл. 4, при нагружении по моде II – в табл. 5.

Таблица 4

Относительные значения составляющих J -интеграла моды I

Table 4

Relative values of the components of the J -integral of mode I

δ 0	ВВ'	BA 1	B’A 1 ’	A 1 A 5	A 1 ’A 5 ’
2∙10-3	1,0476	0,0117	0,0117	0,0008	0,0008
2∙10-4	1,0022	0,0105	0,0105	0,0007	0,0007
2∙10-5	0,9940	0,0103	0,0103	0,0007	0,0007
2∙10-6	0,999	0,0102	0,0102	0,0006	0,0006

Таблица 5

Относительные значения составляющих

J -интеграла моды II

Table 5

Relative values of the components of the J -integral of mode II

δ 0	ВВ'	BA 1	B’A 1 ’	A 1 A 5	A 1 ’A 5 ’
2∙10-3	0,5257	0,0059	0,0028	0,0040	0,0012
2∙10-4	0,8949	0,0071	0,0059	0,0042	0,0031
2∙10-5	0,9716	0,0071	0,0068	0,0041	0,0037
2∙10-6	0,9838	0,0071	0,0071	0,0040	0,0039

Результаты вычисления относительного значения компонент J -интеграла представления (4) для слоистого композита при КЭ-решении на основе модели [30] к решению ANSYS для трещины в виде математического разреза, см. табл. 2, от относительной толщины адгезионного слоя δ ₀ при нагружении по моде I приведены в табл. 6, при нагружении по моде II – в табл. 7.

Из табл. 6, 7 видно, что в модели с адгезионным слоем, модуль упругости которого значительно меньше модуля упругости материала консолей E/Eadh = 100, основной вклад (более 98 %) в представление (4) вносит его первый член. Погрешность вычисления первого слагаемого представления (4) для слоистого композита при 50 = 2 -10—6 между решениями по ANSYS и МКЭ на основе модели [30] составляет: 0,41 % при нагружении по моде I; 0,44 % – по моде II.

Таблица 6

Относительные значения составляющих J -интеграла моды I

Table 6

Relative values of the components of the J -integral of mode I

δ 0	ВВ'	BA 1	B’A 1 ’	A 1 A 5	A 1 ’A 5 ’
2∙10-3	1,0525	0,0054	0,0042	0,0010	0,0003
2∙10-4	1,0041	0,0050	0,0039	0,0009	0,0003
2∙10-5	0,9962	0,0052	0,0041	0,0010	0,0004
2∙10-6	0,9949	0,0078	0,0078	0,0016	0,0006

Таблица 7

Относительные значения составляющих

J -интеграла моды II

Table 7

Relative values of the components of the J -integral of mode II

δ 0	ВВ'	BA 1	B’A 1 ’	A 1 A 5	A 1 ’A 5 ’
2∙10-3	0,5311	0,0052	0,0027	0,0001	0,0001
2∙10-4	0,8959	0,0060	0,0059	0,0001	0,0004
2∙10-5	0,9745	0,0060	0,0063	0,0001	0,0005
2∙10-6	0,9795	0,0059	0,0062	0,0001	0,0005

Заключение

Для модельного представления трещиноподобного дефекта в виде физического разреза с толщиной, рассматриваемой в качестве линейного параметра, определена энергетическая характеристика типа J -интеграла, включающая векторы напряжений на свободной поверхности окрестности трещиноподобного дефекта, связанных с решением задачи, в виде интегральных слагаемых на торцевой части и двух поверхностях физического разреза. Для МКЭ-решения показана близость величины энергетической характеристики при стремлении линейного параметра к нулю к известным значениям J -интеграла для представления трещины в виде математического разреза при модах нагружения I и II. Для физического разреза в материале с однородными механическими характеристиками аддитивные слагаемые имеют одинаковый порядок величины при большем значении на торцевой части. Если материальный слой, лежащий на продолжении физического разреза, имеет существенно меньший модуль упругости по отношению к сопрягаемому слою материалу, то аддитивное слагаемое торцевой части фактически определяет энергетическую характеристику. В случае рассмотрения сопряжения тел тонкими адгезионными слоями, чьи модули упругости, как правило, значительно уступают характеристикам несущих материалов, рассмотренную энергетическую характеристику в торцевой части дефекта адгезионного слоя для МКЭ-решения можно отождествлять со значением J -интеграла слоя нулевой толщины.