К настройке широтно-импульсных модуляторов в релейно-импульсных системах автоматического регулирования металлургических печей
Автор: Панферов В.И., Панферов С.В.
Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy
Рубрика: Металлургическая теплотехника и теплоэнергетика
Статья в выпуске: 3 т.23, 2023 года.
Бесплатный доступ
Введение. В системах автоматизации металлургических печей широко применяются релейно-импульсные регуляторы, содержащие в своем составе исполнительные механизмы (ИМ) постоянной скорости. В данной работе рассматривается задача формализации процедуры настройки широтно-импульсного модулятора (ШИМ), работающего в составе такого регулятора. Структура ШИМ содержит сумматор, интегратор и трехпозиционный релейный элемент (РЭ), имеющий зоны возврата в левой и правой частях его характеристики. Цель исследования. Установить зависимости скважности и периода следования импульсов от характеристик структурных элементов ШИМ. Оптимизация настройки ШИМ способствует как повышению качества переходных процессов в системах автоматического регулирования, так и улучшению их режима работы, что в конечном счете приводит к повышению эффективности работы печей. Материалы и методы. Выполнен обзор литературных данных по рассматриваемой проблеме. Проведен физико-математический анализ процессов, протекающих в указанной структуре ШИМ. Результаты. Установлены зависимости, описывающие режим работы ШИМ от параметров содержащихся в нем элементов. В частности, показано, что с увеличением зоны возврата, а также и постоянной времени интегрирования интегратора период следования импульсов однозначно растет, а вследствие этого частота включения исполнительного механизма снижается. Вместе с тем с увеличением уровня выходного сигнала РЭ период уменьшается, а частота включения исполнительного механизма, наоборот, увеличивается. Показана привлекательная рациональность используемого в регулирующих микропроцессорных контроллерах типа РЕМИКОНТ подхода к задаче широтно-импульсной модуляции. Заключение. Полученные соотношения могут быть использованы для алгоритмизации процедуры настройки рассматриваемого типа ШИМ, что способствует повышению как качества регулирования технологических параметров металлургических печей, так и снижению износа исполнительного механизма и его пуско-регулирующей аппаратуры.
Широтно-импульсная модуляция, релейно-импульсный регулятор, исполнительный механизм постоянной скорости, период следования импульсов, минимальная длительность импульсов, настройка, скважность, качество автоматического регулирования
Короткий адрес: https://sciup.org/147241799
IDR: 147241799 | УДК: 620.9:658.011.56 | DOI: 10.14529/met230307
Текст научной статьи К настройке широтно-импульсных модуляторов в релейно-импульсных системах автоматического регулирования металлургических печей
Постановка задачи
В системах автоматизации металлургических печей, как то в системах автоматического регулирования (САР) температуры и давления в рабочем пространстве, в САР соотношения «топливо – воздух» и др., широко применяются релейно-импульсные регуляторы, содержащие в своем составе исполнительные механизмы (ИМ) постоянной скорости [1–7]. При этом в таких регуляторах для формирования любого частного закона регулирования из семейства пропорционально-интегрально-дифференциальных законов (ПИД-законов) используется широтно-импульсный принцип управления ИМ, вследствие этого такой ИМ ведет себя как интегрирующее звено [8]. Предвключенная часть регулятора в этом случае должна работать по закону ПД или ПДД2. Однако такая реализация типовых законов регулирования является достаточно приближенной, степень близости фактического и идеального законов не всегда является удовлетворительной, при эксплуатации таких регуляторов возникает ряд существенных проблем [9–17]. Так, например, чем меньше период следования импульсов, формируемых широтно-импульсного модулятором (ШИМ) регулятора, тем ближе реальный регулятор к идеальному. Вместе с тем при этом увеличивается частота срабатывания коммутирующей аппаратуры (пускателя) и включений ИМ, что весьма нежелательно, так как приводит к повышенному износу этих технических средств. Кроме того, в процессе работы САР также возможны такие ситуации, когда ШИМ формирует управляющие импульсы настолько малой длительности, что ИМ просто не в состоянии их отработать. Все это приводит к заметному снижению качества, в том числе и точности регулирования, что весьма нежелательно и приводит к уменьшению эффективности работы печей. Здесь для понимания значимости проблемы необходимо привести следующие данные. Известно, например, что «…только автоматическая стабилизация … задания (температуры рабочего пространства) позволяет повысить производительность методической печи на 5…6 % при одновременном снижении удельного расхода топлива на 6…9 %» [5, с. 137], что «…стабилизация коэффициента расхода воздуха (или, что то же самое, соотношения «топливо – воздух») позволила снизить расход условного топлива на 3,2 кг на 1 т отжигаемого металла» в колпаковых печах [18, с. 126] и др.
При наличии статической ошибки регулирования заданное значение давления в печи будет отрабатываться САР не достаточно точно. Вместе с тем известно, что излишне высокое давление в рабочем пространстве нагревательных печей приводит к выбиванию продуктов сгорания, что наряду с ростом тепловых потерь вызывает ускоренный износ конструкций печи, затрудняет визуальный контроль и обслуживание печей, загрязняет атмосферу цеха. Излишне же низкое давление обуславливает подсос в печь через рабочие окна и различные неплотности в кладке холодного воздуха, это ведет к понижению температуры печи, местному охлаждению металла и кладки и увеличению окалинообразова-ния. Кроме того, при этом затрудняется управление процессом горения, так как подсос воздуха приводит к изменению коэффициента расхода воздуха.
Таким образом, все это указывает на необходимость обеспечения высокого качества, в том числе и точности регулирования, что определяется, в первую очередь, настройками регуляторов технологических параметров.
Указанные реальные особенности работы релейно-импульсных регуляторов, влияющие на точность реализации ПИ- и ПИД-законов регулирования, обуславливаются следующим. Как это указано в [9], «…причина заключается в „жестком“ алгоритме широтно-импульсной модуляции», реализуемом в стандартных (классических) релейно-импульсных регуля- торах, т. е. в составе регуляторов необходимо применение настраиваемого ШИМ. По существу такое же заключение содержится и в работах [10–14]. Так, в работе [10] отмечено, что «…следует различать динамическую точность регулирования, зависящую от инерционности объекта регулирования и времени Тим полного хода исполнительного механизма, и статическую точность регулирования, … прямо пропорционально зависящую от минимальной длительности импульса Тимп в блоке ШИМ и обратно пропорционально – от времени Тим полного хода ИМ», что «…повы-шение эффективности работы системы регулирования может быть обеспечено путем оптимизации величины минимальной длительности импульса в зависимости от скорости изменения ошибки регулирования в канале регулирования, что позволит уменьшить частоту включения электродвигателя механизма, повысить точность позиционирования исполнительного механизма и качество работы системы автоматического регулирования». В работе [11] указано на необходимость коррекции характеристик (параметров настройки) ШИМ, в частности, предлагается использовать «…корректор длительности управляющего импульса» и «…алгоритм коррекции, который рассчитывает период ШИМ».
В работе [12] указано, что реальные характеристики релейно-импульсных ПИД-регуляторов существенно зависят от свойств ИМ постоянной скорости, его режима работы, что в значительной мере определяется параметрами широтно-импульсного управления.
В работе [13] отмечено, что динамические характеристики релейно-импульсных ПИ-регуляторов «…в области высоких частот и малых отклонений регулируемого параметра существенно отличаются от характеристик идеальных ПИ-регуляторов».
В работе [14], в частности, «…даны рекомендации для автоматической подстройки длительности импульсов и параметров релейного элемента регулирующего блока в ходе процесса регулирования… Приведенные рекомендации обеспечивают существенное снижение частоты включений ИМ в процессе регулирования». Здесь при настройке РЭ применялось изменение его зоны нечувствительности и зоны возврата (ширины петли гистерезиса).
Подчеркнем также, что именно из-за проблем технической реализации и порождаемых ими проблем эксплуатации релейно-импульсных ПИ- и ПИД-регуляторов в работе [15] предложен другой подход к решению задачи реализации, здесь предлагается «…рассмат-ривать ИМ как пропорциональное звено», утверждается, что «…в этом случае реализация ПИД-регулятора существенно упрощается».
Таким образом, вполне очевидно, что задача повышения качества и надежности работы релейно-импульсных регуляторов может быть решена, в том числе за счет применения в их составе параметрически настраиваемого ШИМ. В современных условиях это не является проблематичным, так как применяемые в настоящее время управляющие устройства в подавляющем большинстве случаев представляют собой программно-аппаратные средства [16]. Вместе с тем достаточно очевидно, что для удовлетворительного решения задачи необходимо бы знать, как конкретно параметры настройки ШИМ влияют на период следования и длительность управляющих импульсов, подаваемых (через пускатель) на исполнительный механизм постоянной скорости. Некоторое решение этой проблемы можно найти, например, в работе [17]. Однако в этой работе учтены не все реальные характеристики релейных элементов (РЭ), включаемых в состав программно-аппаратного регулирующего блока, в частности, в работе [17] считается, что зона нечувствительности РЭ равна его двум зонам возврата, что далеко не всегда так, размер зоны нечувствительности, как правило, заметно больше. Кроме того, у такого РЭ есть только один параметр настройки – изменяя величину зоны возврата, мы будем изменять и размер зоны нечувствительности и, наоборот, изменяя размер зоны нечувствительности, мы будем менять и величину зоны возврата.
Решение задачи
Структурная схема рассматриваемого регулирующего блока (РБ) ПИ-регулятора с подключенным исполнительным механизмом (ИМ) постоянной скорости приведена на рис. 1.
На рис. 1: ПД – пропорциональнодифференциальный блок; х и е - соответственно входной и выходной сигналы ПД-блока; Сум - сумматор; усум - выходной сигнал сумматора; Инт - интегратор; хинт и уинт - соответственно входной и выходной сигналы интегратора; Х р Э и у р Э - соответственно входной и выходной сигналы релейного элемента; ц - положение выходного вала ИМ.
Такой регулирующий блок может быть реализован как аппаратным, так и программно-аппаратным способами.
Характеристика релейного элемента (РЭ), входящего в состав ШИМ, приведена на рис. 2.
На рис. 2: Д в - порог срабатывания (включения) РЭ; Дн - порог выключения (порог возврата [2]) РЭ; Д в — Дн - ширина петли гистерезиса (зона возврата); —Дв ^ + Д в -размер зоны нечувствительности РЭ; А - уровень выходного сигнала РЭ.
Рассмотрим работу ШИМ только для случая, когда работает правая часть характеристики РЭ. Для левой отрицательной части РЭ работает аналогично.
Пусть вначале РЭ выключен, т. е. его выходной сигнал равен нулю урэ = 0, поэтому на вход интегратора будет поступать только сигнал е , вследствие этого уинт = —t (В дан- ин 1 т0 '
ном случае учитывается, что сигнал е изменяется значительно медленнее, чем процессы переключения РЭ, поэтому приближенно полагается, что е = const [17, 19]), здесь t -время, Го - постоянная времени интегрирования интегратора, входящего в состав ШИМ.
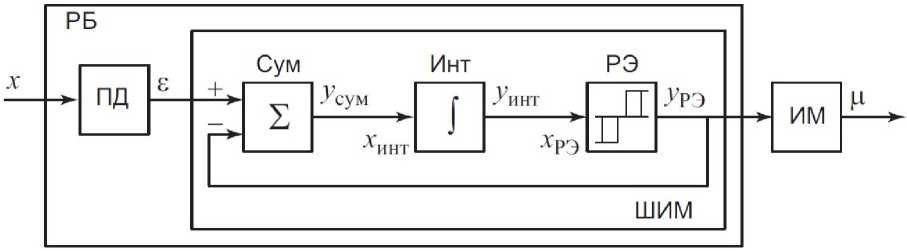
Рис. 1. Структурная схема РБ с подключенным ИМ постоянной скорости
Fig. 1. Block diagram of a working unit with a connected constant speed actuator
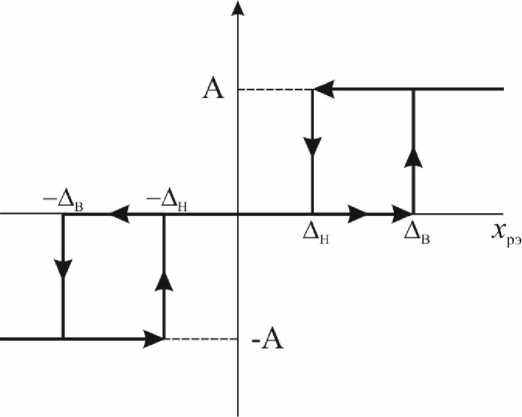
Рис. 2. Характеристика РЭ
Fig. 2. Characteristics of the relay element
РЭ будет выключен до тех пор, пока сигнал на выходе интегратора не достигнет значения Дв, т. е. должно выполняться условие
-(П = ДВ, (1)
^ П в где tn - длительность паузы. Поэтому длительность паузы будет равна tn = '. (2)
Далее включаются РЭ и ИМ. После этого сигнал на входе интегратора будет уже равен (е — Д), поэтому его выход будет изменяться в соответствии с выражением
Уинт = Ав +-- 1 = Дв--t, (3)
ин т в ^ в ^
выход будет убывать так как Д > е . Этот сигнал будет убывать до Дн, т. е. до момента выключения РЭ и остановки ИМ. Поэтому длительность как первого!!! , так и последующих импульсов будет равна
Дв —— tH = Дн ^ t„ = ' . (4)
в То и н и -_ £
Здесь нужно иметь в виду, что должно быть е < Д, в противном случае формула (4) будет совершенно бессмысленной, так как при е > Д длительность импульсов будет отрицательной, что, очевидно, никак невозможно.
Примечание. При такой постановке задачи никак не допустимо полагать, что сигнал е может быть равен нулю: в таком случае РЭ никогда не включится!!! Однако в работе [17] это обстоятельство никак не учитывается и при вычислении минимальной длительности импульсов полагается е = 0 . Кроме того, если же РЭ уже включен и при 72
таком его состоянии сигнал е станет рав-
ным нулю, то по истечении некоторого времени РЭ просто выключится и опять в ближайшее время не включится, импульсный режим работы регулятора наблюдаться не (Дв_Д )^1
будет. Поэтому значение-------- это дли тельность только одного импульса для этой
ситуации .
Далее на вход интегратора опять будет
поступать только сигнал е , вследствие его выход будет увеличиваться в соответствии с вы-
ражением
У инт = Д н + ^Т t
и опять-таки до того момента, как
Д н + ^ = Д в . (6)
Поэтому длительность второй паузы уже будет равна
t
п =
(Дв Д н )Т о
.
£
Далее включаются РЭ и ИМ, длитель-
ность импульса будет прежней. При этом период следования импульсов будет равен
Г = tИ + tn =
(Д в _Д н )Т о -
-£_£2
(Дв Д н )Т о j (Дв Д н )Т о -_£ £
Анализ полученных результатов
Как это следует из формулы (8), период следования импульсов Г зависит от е . При этом параметрами настройки периода следования импульсов Г, равно как и их частоты, являются величины Дв, Дн, Го и Д. Как это нетрудно видеть, с увеличением разности
(Дв-Дн), а также и постоянной времени интегрирования интегратора Г0 период следования импульсов Г однозначно растет (а час- тота, понятно, уменьшается). Вместе дТ (Д^—Д )тпе2 „ м = (А—£)2£2 < 0, следовательно, личением уровня выходного сигнала период Г уменьшается.
Скважность импульсов
Си 1 £
Y = — = ---— = -,
-
1 Т 1 + Сп/С и А’
с тем
с уве-
РЭ Л
как это следует из (9), тоже зависит от е .
Из (4) и (9) следует, что с уменьшением сигнала е длительность импульсов и их скважность тоже уменьшаются, причем здесь необходимо иметь в виду, что должно быть е < Л, в противном случае формула (4) для длительности импульсов теряет всякий смысл. Зависимость периода следования импульсов Г от е экстремальная, здесь критическая точка будет дТ = (Дв-Дн)Т)А(-А + 2£)
де
= 0 ^ Екрит = 2 . (10)
(а-е)2е2
При этом, как это нетрудно видеть, при е < А будет ^Т < 0, а при е > А будет ЗТ > 0.
Следовательно, при е = А период следования импульсов будет принимать минимальное значение, равное
Г мин 4(Дв ДН)Т0
_ А .
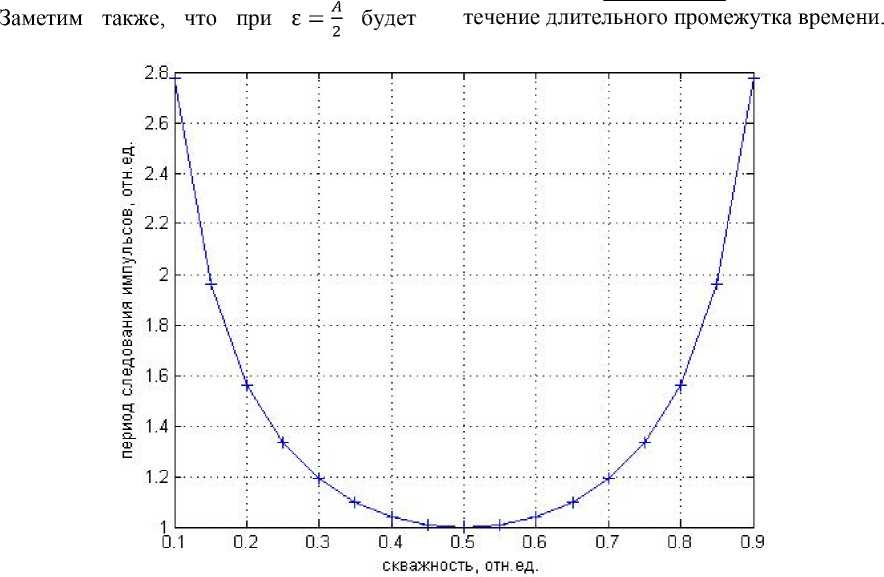
Рис. 3. График зависимости периода следования импульсов от скважности Fig. 3. Graph of the dependence of the pulse repetition period on the duty cycle
С и = С,
• п
_ 2(Дв-Д н )Г0
А
■, а у = 0,5. Это значение
С и в два мального муле (4).
раза больше предельного минизначения, вычисляемого по фор-
Из формулы (9) следует, что при е = 0 будет и у = 0, а поэтому и длительность импульса Си = 0, т. е. согласно данным соотношениям используемой модели процессов в регуляторе минимальная длительность импульсов равна нулю. Вместе с тем если рассмотреть формулу (4), то минимальная дли- тельность импульсов совсем не равна а равна якобы следующей величине limL .о?£ Д ? Т.
Нетрудно установить, что нулю,
Т
а2
от
Тмин 4(А-£)£ 4 С1— 5 )"5 .
Т
График зависимости т мин
£
А = Y приве-
ден на рис. 3. Здесь учтено, что физически обоснованный диапазон изменения е таков: 0 < е < Л.
Из формулы (8) следует, что lim£ > 0 Г = ет; lim£ >А Г = ет, вместе с тем при е ^ 0 Y ^ 0, поэтому РЭ будет находиться в выключенном состоянии, причем в течение довольно длительного промежутка времени, так как при е ^ 0 Г ^ ет . При е ^ Л Г ^ ет, а Y ^ 1 — РЭ находится во включенном состоянии также в
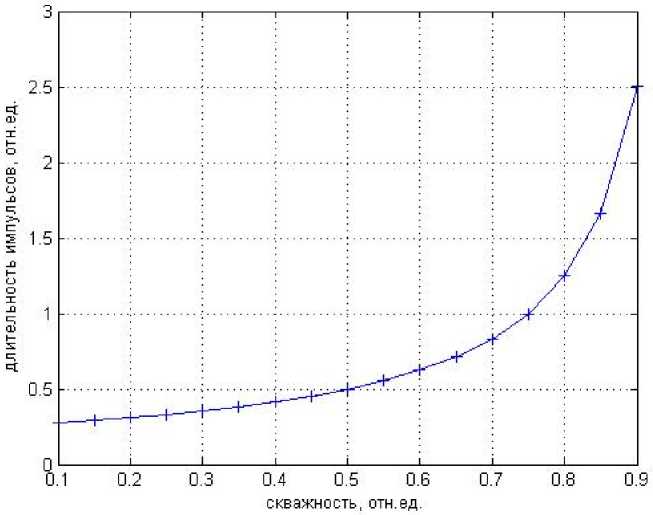
Рис. 4. График зависимости длительности импульсов от скважности Fig. 4. Graph of pulse duration versus duty cycle
Можно также показать, что tи _ A _ 1
Тмин 4(A-£) 4(1- | ) .
График зависимости т мин от ден на рис. 4.
Нетрудно видеть, что -мин
£
A = Y приве-
t и . A ^ ^ мин £
Т = tи • A => Т = у => tи = yT. Так и должно быть. Это подтверждает приемлемость используемых для описания работы ШИМ соотношений. Вместе с тем следует отметить, что согласно рис. 3а работы [17] при y = 0 tи Ф 0, что никак не должно быть, так как по опреде- лению tи = yT.
О широтно-импульсной модуляциив Ремиконте Р-130
В работе [9] указано, что реализуемый в Ремиконте Р-130 «…импульсный вывод осуществляет широтно-импульсную модуляцию с переменным периодом. Импульсы подаются таким образом, чтобы при любом значении входного модулируемого сигнала обеспечить равенство либо времени импульса, либо времени паузы минимальному времени импуль-са/паузы, которое задается на настроечном входе алгоритма. При этом если требуется обеспечить скважность менее 50 %, минимальным берется время импульса, более 50 % -время паузы». При этом не совсем ясно, как в Р-130 вычисляется необходимая скважность импульсов? Очевидно, что скважность должна быть функцией выходного сигнала ПД или ПДД2 блоков y = /(£), в рассматриваемом случае Y = а (см. формулу (9)). Если у из- вестна и минимальная длительность импульса tMUH на настроечном входе задана, то Т = ^^~ при y < 0,5. Если же y > 0,5, то tn = tM™ и период следования импульсов будет равен Т = у-^. Все это можно записать с помощью следующих интервальных формул:
при 0 < y < 0,5;
Т = (15)
1-;при 0,5 < Y< 1
или же
т Г ^ при 0 < y < 0,5;
t мин = 1
и у-^при 0,5 т Кривая зависимости tMs от Y, (16) построен- ная по интервальной формуле (16), приведена на рис. 5. Как видно из рис. 5, кривая имеет экстре- мальный характер, минимальное значение периода Тмин (максимальное значение частоты включения ИМ) так же, как и в вышерассмотренном случае, достигается при y = 0,5. При этом минимальное значение периода следования импульсов будет равно Тмин = 2 • t^™. Рис. 5. Зависимость периода следования импульсов от скважности, реализуемая в ремиконтах Fig. 5. Dependence of the pulse repetition period on the duty cycle, implemented in remikonts Следует отметить, что используемый в Р-130 подход к задаче широтно-импульсной модуляции представляется нам достаточно привлекательным: задавая tU™H, при таком подходе исключаем ситуации, когда ИМ не может как отработать переключения из-за их малой длительности, так ограничить минимально возможное значение периода следования импульсов. Выводы Полученные соотношения описывают режим работы РЭ и могут быть использованы для алгоритмизации процедуры настройки рассматриваемого типа ШИМ. В целом за счет этого могут быть повышены качество и надежность работы релейно-импульсных регуляторов в составе автоматизированных систем управления технологическими процессами металлургических печей.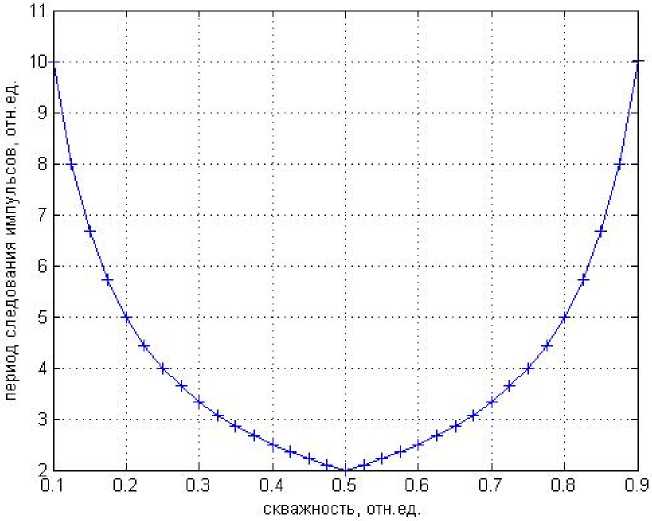
Список литературы К настройке широтно-импульсных модуляторов в релейно-импульсных системах автоматического регулирования металлургических печей
- Проектирование систем контроля и автоматического регулирования металлургических процессов: учеб. пособие / Г.М. Глинков, В.А. Маковский, С.Л. Лотман, М.Р. Шапировский. М.: Металлургия, 1986. 352 с.
- Основы теории и элементы систем автоматического регулирования / В.Ю. Каганов, Г.М. Глинков, М.Д. Климовицкий, А.К. Климушкин; под ред. Г.М. Глинкова. М.: Металлургия, 1987. 270 с.
- Наладка автоматических систем и устройств управления технологическими процессами: справ. пособие / А.С. Клюев, А.Т. Лебедев, Н.П. Семенов, Н.Г. Товарнов; под ред. А.С. Клюева. М.: Энергия, 1977. 400 с.
- Копелович А.П. Инженерные методы расчета при выборе автоматических регуляторов. М.: Металлургиздат, 1960. 190 с.
- Автоматизация методических печей / Л.И. Буглак, И.Б. Вольфман, С.Ю. Ефроймович и др. М.: Металлургия, 1981. 196 с.
- Автоматическое управление металлургическими процессами / А.М. Беленький, В.Ф. Бердников, О.М. Блинов, В.Ю. Каганов. М.: Металлургия, 1989. 384 с.
- Шатохин К.С. Основы теории автоматического управления промышленными печами: учеб. М.: Издат. Дом НИТУ «МИСиС», 2020. 216 с.
- Беляев Г.Б., Кузищин В.Ф., Смирнов Н.И. Технические средства автоматизации в теплоэнергетике: учеб. пособие для втузов. М.: Энергоиздат, 1982. 320 с.
- Разработка и исследование алгоритмов и программ управления исполнительными механизмами систем автоматического регулирования / А.Н. Рыбалев, Д.А. Теличенко, В.Ю. Косицин и др. // Вестник АмГУ. Серия: естественные и экономические науки. 2012. № 57. С. 104–110.
- Голубев А.В. Повышение эффективности работы систем автоматического регулирования с широтно-импульсным модулятором // Вестник Ивановского государственного энергетического университета. 2007. № 4. С. 81–83.
- Горюнов А.Г., Ливенцов С.Н. Цифровой регулятор для системы управления с исполнительным механизмом постоянной скорости // Известия Томского политехнического университета. 2004. Т. 307, № 6. С. 131–134.
- Бочаров М.Г., Панько М.А. Анализ соответствия реальных и теоретических характеристик микропроцессорных ПИД-регуляторов // Теплоэнергетика. 2009. № 10. С. 62–67.
- Александрова Н.Д., Давыдов Н.И. О настройках импульсных релейных регуляторов на малоинерционных объектах // Теплоэнергетика. 2002. № 5. С. 54–57.
- Кузищин В.Ф., Дробилко А.С., Стерлин А.Я. ПИД-регуляторы с исполнительным механизмом постоянной скорости: варианты реализации, автоподстройка длительности импульсов // Теплоэнергетика. 2021. № 5. С. 78–88. DOI: 10.1134/S0040363621050064
- Горбунов А.И. Об алгоритме реализации ПИД-регулятора с исполнительным механизмом постоянной скорости // Промышленные АСУ и контроллеры. 2009. № 3. С. 23–24.
- Ризо А.Е., Золотарев С.В. Обзор современных отечественных ПЛК с поддержкой технологии программирования ISaGRAF 6: соответствие международным стандартам и российские ноу-хау // Автоматизация и IT в нефтегазовой области. 2016. № 2 (24). С. 38–46.
- Бочкарева Е.Ю., Кузищин В.Ф. Настойка длительности импульсов регуляторов с исполнительным механизмом постоянной скорости // Новое в российской электроэнергетике (НРЭ). 2009. № 9. С. 35–47.
- Ревун М.П., Гранковский В.И., Байбуз А.Н. Интенсификация работы нагревательных печей. Киев: Техника, 1987. 136 с.
- Ротач В.Я. Расчет динамики промышленных автоматических систем регулирования. М.: Энергия, 1973. 440 с.


