К обоснованию принципа Маха (вторая редакция)

Установлена зависимость между инертной и гравитационной массами на Земле. Показано, что принцип Маха и принцип эквивалентности инертной и гравитационной масс можно исследовать экспериментально. Первая редакция - см. [1].

Известен принцип Маха, утверждающий, что инертные свойства каждого физического тела определяются всеми остальными физическими телами во Вселенной и зависят от их расположения [1]. Первая идея для проверки этого принципа состоит в том, чтобы временно и подальше убрать все тела Вселенной. Но современной суммы технологий недостаточно для реализации этой идеи. И поэтому (и пока «спасительная» идея о непознаваемости не овладела умами окончательно, как это произошло, например, в квантовой механике) попробуем попытаться понять, как Земля могла бы создавать инерцию (а все остальные тела Вселенной и без нас кто-то отодвинул на достаточное расстояние).

Как Земля могла бы создавать силу инерции, действующую на ускоряющееся тело? Может быть, примерно также, как большой неподвижный электрический заряд на другой ускоряющийся заряд… Ведь известно много аналогий между электродинамикой и гравитомагнетизмом, которые описываются одинаковыми уравнениями Максвелла – см. например [2].

Рассмотрим электрический заряд q , движущийся относительно заряда Q с ускорением а . Напряженность электрического поля Е, создаваемого зарядом q в центре заряда Q, определяется по формуле Лармора [3]. В том случае, когда скорость заряда много меньше скорости света с , формула принимает вид [4]:

Е s а[пх[пха]] 8     С2К ,                                         (1) где R - расстояние между зарядами, а П - орт вектора R, направленного от заряда q к заряду Q - см. рис. 1. Если вектор ускорения а направлен перпендикулярно вектору R, то вектор

Е_о = [п X [п X а]], (2)

и вектор а связаны соотношением

Ео = -а

• - см. приложение. Из (1, 2, 3) сдедует, что на заряд Q со стороны заряда q действует сила

• F. = ^Ео = -^(4)

В силу второго закона Ньютона на заряд q со стороны заряда Q действует сила

F« = -F, = ^а.

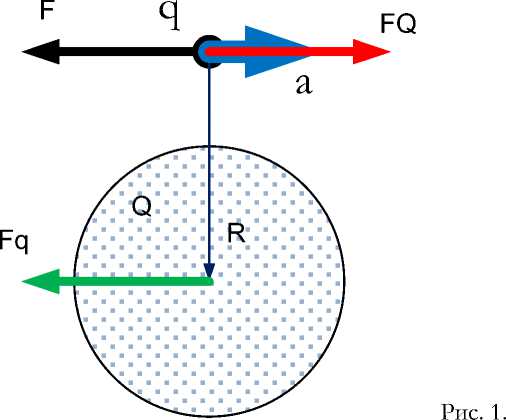
Предположим по аналогии, что ускоренное движение массы также описывается уравнением (1), где q - гравитационная масса, а Е - гравитационная напряженность. Рассмотрим случай, когда масса q движется в поле другой массы Q на расстоянии R ^ ^ от центра этой массы в плоскости, перпендикулярной вектору R. В этом случае применимы все предыдущие выводы. Следовательно, тело Q действует на тело q силой (5) и вектор силы направлен параллельно вектору ускорения а.

Сила тяги, движущая массу q с ускорением а ,

F = mqa,(6)

где m q - инертная масса гравитационной массы q . Таким образом, на массу q действуют две противоположно направленные силы (5, 6). По второму закону Ньютона эти силы должны быть равны, т.е.

таа = -^а q       C2R- ’

или т0 =    .                                  (8) q     C2R                                                   ' ’ Рассмотрим коэффициент в пропорциональности между гравитационной массой и инертной массой. Тогда

q = тД                          (9) Q =mQe.                                 (10)

Из (8, 9, 10) получаем:

_ e²m_qm_Q

т C 2 R ,                                  (■') в =   R                                   (12)

Например, для Земли имеем:

Q Тогда

— 6 • 1024 кг, R « 6 • 107 м, с — 3 • 109 м/с .

7—24

в = с l^R — 3 • 10⁹ • 10~ — 1.            (13)

Таким образом, наша аналогия не противоречит принципу эквивалентности гравитационной и инертной масс. И мы показали, что в некотором частном случае принцип Маха выполняется: инертная масса определяется гравитационной массой и размером Земли. Формула (12) дает возможность установить зависимость инертной массы конкретного тела от параметров внешних тел и тем самым определить характер этой зависимости и границы применимости принципа Маха.

Таким образом, изложенное показывает, что принцип Маха может быть проверен экспериментально и вместе с тем может быть экспериментально проверен принцип эквивалентности инертной и гравитационной масс.

Приложение

Пусть вектор П в декартовой системе координат направлен по оси OZ , а вектор а направлен по оси ОХ , как показано на рис. 1. Тогда запишем эти векторы в следующем виде:

п = [0,0, -1],

а = [а%, 0,0]

и найдем

[п х а] = [0, ах, 0],

[п х [П х а]] = [[0,0, -1] х [0, ах, 0]] = [-ах, 0,0].

Следовательно,

Ео = [п х [п х а]] = -а.