К оценке однородности количественной статистической совокупности и информативности её среднего значения
Автор: Долгов В.В.
Журнал: Физическая культура, спорт - наука и практика @fizicheskaya-kultura-sport
Рубрика: Теория и методика профессионального образования
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14264071
IDR: 14264071
Текст статьи К оценке однородности количественной статистической совокупности и информативности её среднего значения
Введение. Во всех исследованиях при отборе объектов для разработки норм на основе средних арифметических значений (САЗ) и при комплектовании контрольных и экспериментальных групп необходимо оценивать репрезентативность этих объектов по отношению к изучаемому количественному признаку. Особенно это важно, если в дальнейшем для статистической обработки планируется применение параметрических методов математической статистики, основанных на нормальном распределении. Репрезентативность таких групп обычно отождествляется с однородностью совокупностей, данные которых являются результатами измерений признака у каждого объекта в шкалах интервалов или отношений. В настоящее время оценивают однородность этих совокупностей в основном по их коэффициентам вариации. При этом нет единого мнения, при какой его величине совокупность считать однородной. В данной работе предлага- ется новый показатель однородности количественной статистической совокупности, информативности её САЗ и аргументация конкретной его оценки в случае нормальности совокупности.
Результаты исследования. Пусть имеем объём n статистическую совокупность количественных случайных данных xi (i=1, 2, … n), каждое из которых – результат измерения изучаемого статистического признака х. Представим её в неубывающем виде значений, графически отложенных на прямой линии в определённом масштабе от точки отсчёта – начала координат О, совпадающим с х=0. Определим минимальное xmin и максимальное xmax значения этой ранжированной совокупности и выделим в ней два интервала [0, xmin) (1) и [xmin, xmax] (2). Предположив, что за пределами интервала (2) значения признака и переменной xi либо невозможные, либо достоверные, можно утверждать, что xi варьирует только во втором – вариативном интервале, в котором находится САЗ – х=(Σxi)/n (3) рассматриваемого признака и совокупности. Размахом этого интервала является R=xmax–xmin (4). Так как в интервале (2) находятся все вариативные особенности совокупности, то есть смысл подвергать анализу в основном его. Выберем на графике новое начало координат О’, совпадающее со значением xmin – точкой приведения, и рассмотрим имеющуюся совокупность в новой, приведённой к xmin, системе координат. В ней все координаты x’, в отличие от координат х основной системы с центром О, уменьшены на xmin. В связи с этим и данные совокупности будут уменьшены на xmin. Поэтому совокупность и все её характеристики в основной системе можно назвать основными, а совокупность и все её характеристики в приведённой системе назвать приведёнными. Такое преобразование связывает данные приведённой совокупности с данными основной равенством x’i=xi-xmin (5) и приведённое среднее арифметическое значение (ПСАЗ) – х’ с основным САЗ – х равенством х’= х-xmin (6). Главный смысл этого преобразования состоит в том, что оно отсекает интервал (1), но оставляет инвариантными основные вариационные характеристики: объём n, размах R, дисперсию σ², стандартное отклонение σ, ошибку репрезентативности mх ̅ =mх ̅ ’. Такое преобразование системы координат используется во всех непараметрических критериях статистики, где результаты измерения переводятся в ранги одной системы координат с началом в точке, равной единице.
В связи с тем что невариационный интервал (1) находится в знаменателе общепринятого безразмерного показателя однородности совокупности, основного коэффициента вариации (ОКВ) в виде v=σ/х (7) или v =σ*100 %/ х (7’), то он неоправданно уменьшает в зависимости от значения xmin величину ОКВ. Это приводит к тому, что явно неоднородная совокупность при относительно большой величине интервала (1) может быть признана однородной, а САЗ основной совокупности не будет объективно отражать средний уровень изучаемого признака, т. е. будет неинформативным. Под информативностью любой характеристики по- нимается её свойство объективно отражать то, ради чего она вводится. В этом случае выводы, полученные с использованием такой совокупности, могут оказаться неадекватными действительности даже при формально хорошей их достоверности. Поэтому предлагается принимать в качестве показателя однородности количественной статистической совокупности приведённый коэффициент вариации (ПКВ) в виде v’=σ/ х’ (8) или v’=σ*100%/ х’ (8’). Он учитывает вариативность совокупности и в числителе, и в знаменателе и не зависит от интервала (1). По его величине можно объективно сравнивать однородности и информативности САЗ любых количественных статистических совокупностей как генеральных, так и выборочных, как нормально распределённых, так и не относящихся к нормальному распределению. В общем случае, при какой величине v’ совокупность считать однородной, а её САЗ информативным, каждый исследователь оценивает самостоятельно.
В математической статистике краткое представление о статистической совокупности принято приводить в виде (х±mх ̅ , n) (9). В связи с введением определений основных и приведённых характеристик предлагается такое представление приводить в виде (х, σ, xmin, xmax, n) (10). В нём достаточно полно отражены основные особенности рассматриваемой совокупности и содержится достаточно информации об её вариативном интервале. Естественно, что при повторных измерениях изучаемого признака границы вариационного интервала будут меняться. Эти изменения вызовут изменение значений σ, х’, v’, что отразится на информативности САЗ. При репрезентативности группы объектов измерения значительного изменения информативности САЗ не произойдёт.
В случае, когда имеющиеся совокупности нормально распределённые и к их анализу планируется применение соответствующих параметрических методов, можно через величину ПКВ стандартизировать их однородности и информативности САЗ, опираясь на свойства закона нормального распределения вероятностей случайных величин [1, 4]. На основании этого закона всегда можно рассчитать вероятность попадания конкретной случайной величины х нормально распределённой совокупности в любой выбранный интервал её значений из области (– ∞≤ х ≤ +∞) (рис.1).
Как видно из рисунка 1, вероятность попадания случайной величины в закрытый интервал [х-3σ, х +3σ] (11), где х – среднее арифметическое, σ – стандартное отклонение распределения, равна 99,72 %. Если пренебречь «хвостами» значений (х ≤ х – 3σ) и (х +3σ ≤ х), выходящими слева и справа от х за пределы интервала (11) с суммарной вероятностью всего 0,28 % и считая их значения выбросами или артефактами (по правилу трёх сигм), то область (11) можно принять за основной вариационный интервал нормального распределения (ОВИНР). Определяя левую крайнюю точку этого интервала как xmin= х -3σ (12), а правую – как xmax= х +3σ (13), получим, что размах ОВИНР и основное его САЗ
Рисунок 1.
Вероятность попадания случайной величины х в соответствующие интервалы нормального распределения, обозначенные стрелками
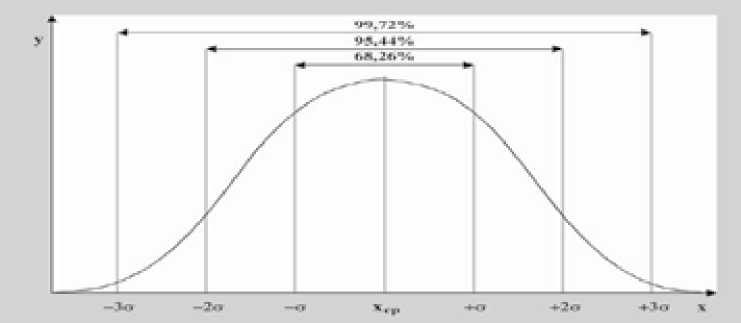
Рисунок 2.
ОВИНР для х=24,3; σ =1,5; ∆х=0,5 (значения горизонтальной оси соответствуют центрам интервалов)
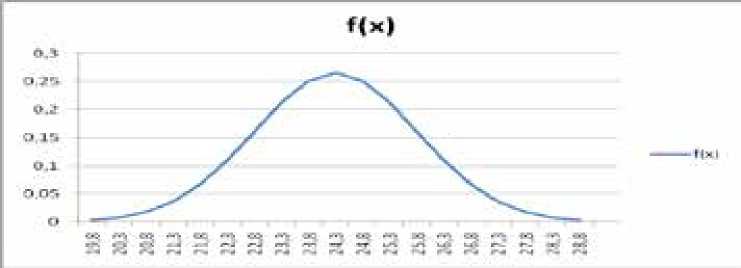
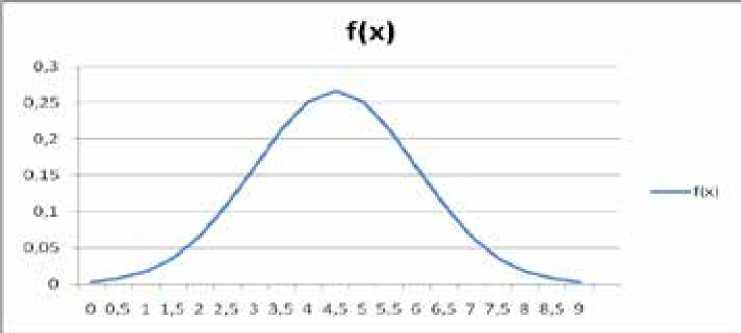
Рисунок 3.
ПВИНР для х’=4,5; σ=1,5; ∆х=0,5 (значения горизонтальной оси соответствуют центрам интервалов)
соответственно будут иметь вид: R=xmax–xmin=6σ (14), х=(xmax+xmin)/2 (15). Построим новую, приведённую систему координат х’о’у’, начало которой совместим с xmin, оставив неизменными направления осей абсцисс и ординат. Т. к. координаты системы хоу связаны с координатами системы х’о’у’ соотношениями (у=у’, х=х’+xmin) (16), то х ̅ ’ – среднее значение приведённого вариационного интервала нормального распределения (ПВИНР) – примет вид х’= х-xmin=3σ (17).
Аналогичным образом выбрано сравнительно легко табулируемое стандартное нормальное распределение с началом координат в точке х и σ=1. Общий вариационный интервал этого распределения с точкой приведения О’, совпадающей со значением х = -3σ и приведённым САЗ х’=3, будет иметь вид [-3σ, 3σ].
В качестве иллюстрации рассмотрим пример 1 для конкретных значений параметров х и σ нормального распределения, представленный на рисунке 2.
В данном случае получим, что все значения случайной переменной х, принадлежащие «хвостам», в зависимости от смысла рассматриваемого признака, чем больше – тем лучше или чем больше – тем хуже, соответственно являются либо достоверными, либо невозможными и не влияют на вариацию переменной в интервале [19,8; 28,8]. Переместив начало координат х=0 в точку xmin=19,8=х’=0, из (17) получим х’=4,5 и график ПВИНР, изображённый на рисунке 3. Стандартное отклонение σ=1,5 осталось прежним на основании своего свойства.
Графики функции y=f(x) и y=f(х’), соответственно изображённые на рис. 2 и рис. 3, при наложении совпадают в соответствии с особенностями нормальных распределений с одинаковыми стандартными отклонениями и разными средними значениями. Их можно назвать эквивалентными. В таких видах можно представить нормальное распределение для любой конкрет- ной пары значений параметров х, σ. По правилу трёх сигм в ПВИНР нет артефактов, а его ПКВ имеет вид v’=σ/ х’=σ/3σ=1/3 (18) или v’=(1/3)*100%≈33,3% (18’). Из этого следует, что стандартное отклонение основных вариационных интервалов всех нормальных распределений должно быть в три раза меньше их приведённых САЗ. Такое утверждение даёт возможность принять значение v’ в виде (18) или (18’) в качестве максимального для того, чтобы ПВИНР считать однородным. Перенося вышеизложенное на любую нормально распределенную статистическую совокупность со значениями х, σ, можно и для её значения ПКВ в виде (18) или (18’) взять предельными для того, чтобы эту совокупность считать однородной, а её САЗ информативным.
В итоге получаем: нормальную количественную статистическую совокупность можно считать однородной и её САЗ информативным, если для приведённого вариационного интервала совокупности выполняется условие: 0≤v’≤1/3 (19) или 0%≤v’≤33,3 % (19’). Исходя из (19) и (19’), предлагается следующая линейная четырёхбалльная градация однородности статистической совокупности и информативности её среднего значения:
-
1) если 0 %≤v’≤11,1 % (20), т. е. 0≤v’≤1/9 (20’) – однородность совокупности и информативность её САЗ отличная;
-
2) если 11,1 %≤v’≤22,2 % (21), т. е. 1/9≤v’≤2/9 (21’) – однородность совокупности и информативность её САЗ хорошая;
-
3) если 22,2 %≤v’≤33,3 % (22), т. е. 2/9≤v’≤1/3 (22’) – однородность совокупности и информативность её САЗ) удовлетворительная;
-
4) если v’≤33,3%(23), т. е. v’≤1/3 (23’) – однородность совокупности и информативность её САЗ неудовлетворительная .
В последнем случае САЗ количественной совокупности определено формально и является неинформативным для оценки уровня её признака. Его самостоятельное использование или использование в любом параметрическом методе математической статистики может привести к неадекватным выводам, т. к. взятая для анализа совокупность неоднородная, в ней использованы вариационные артефакты. Какому уровню однородности, т. е. величине v’, придерживаться, исследователь решает сам в зависимости от особенностей своего эксперимента. Все официальные средние значения и нормы должны определяться на основе работы с однородными совокупностями.
Выбрав уровень однородности совокупности, исследователю необходимо, для возможности использования параметрических методов, убедиться в том, что данная совокупность является нормально распределённой. Часто исследователи не проводят эту проверку из-за убеждённости, что она трудоёмкая и априори предполагают это условие выполненным. Такая халатность может привести к тому, что полученные выводы не будут соответствовать действительности.
В арсенале математической статистики имеется много критериев согласия, с помощью которых определяют принадлежность выборки к нормальному распределению [1]. Одним из них является двусторонний критерий Дэвида – Хартли – Пирсона, который сравнительно простой в применении и достаточный по мощности [1, с. 258, с. 278; 2; 3]. В связи с незаслуженно редким практическим использованием этого критерия ниже приводится основная информация о нём. Статистика этого критерия имеет вид U=R/σ (24). Гипотеза о принадлежности взятой совокупности к нормальному закону распределения принимается с определённым уровнем значимости α, если U1(α)≤U≤U2(α) (25). В противном случае она отвергается с этим же α. Для оценки U можно использовать таблицу с уровнем значимости α = 0,05, где n – объём совокупности [1, с. 259; 3, с. 491].
Если принять изложенные выше рассуждения, то можно сделать следующий вывод: для определения принадлежности статистической совокупности к нормальному распределению по критерию Дэвида –
Таблица
Критические границы U1(α ) и U2(α ) критерия Дэвида – Хартли – Пирсона с уровнем значимости α = 0,05
|
n |
U1 |
U2 |
n |
U1 |
U2 |
n |
U1 |
U2 |
|
3 |
1,758 |
1,999 |
16 |
3,010 |
4,240 |
65 |
4,010 |
5,570 |
|
4 |
1,980 |
2,429 |
17 |
3,060 |
4,310 |
70 |
4,060 |
5,630 |
|
5 |
2,150 |
2,753 |
18 |
3,100 |
4,370 |
75 |
4,130 |
5,68- |
|
6 |
2,200 |
3,012 |
19 |
3,140 |
4,430 |
80 |
4,150 |
5,730 |
|
7 |
2,400 |
3,222 |
20 |
3,180 |
4,490 |
85 |
4,200 |
5,780 |
|
8 |
2,500 |
3,399 |
25 |
3,30 |
4,710 |
90 |
4,240 |
5,820 |
|
9 |
2,590 |
3,552 |
30 |
3,470 |
4,890 |
95 |
4,270 |
5,860 |
|
10 |
2,670 |
3,685 |
35 |
3,580 |
5,040 |
100 |
4,310 |
5,900 |
|
11 |
2,740 |
3,800 |
40 |
3,670 |
5,160 |
150 |
4,59 |
6,18 |
|
12 |
2,800 |
3,910 |
45 |
3,750 |
5,260 |
200 |
4,78 |
6,38 |
|
13 |
2,860 |
4,000 |
50 |
3,830 |
5,350 |
500 |
5,37 |
6,94 |
|
14 |
2,920 |
4,090 |
55 |
3,900 |
5,430 |
1000 |
5,79 |
7,33 |
|
15 |
2,970 |
4,170 |
60 |
3,960 |
5,510 |
Хартли – Пирсона, уровня её однородности и информативности её среднего арифметического значения необходимо и достаточно знать характеристики этой совокупности в виде (10). Всё остальное определяется по соответствующим формулам и таблице.
В случае нормальности, но неоднородности основной совокупности, т. е. её v’ 33,3 %, для продолжения анализа из неё выявляют вариационные артефакты и выделяют однородную, может быть и не одну, статистическую выборку, пользуясь выбранной градацией v’. Такая процедура относится к процессу группировки статистических данных. Для иллюстрации такого подхода рассмотрим конкретный пример.
Пример 1. Из десяти лучших результатов, показанных на чемпионате России по лёгкой атлетике в прыжках в высоту, выделить группу сильнейших прыгунов отличной однородности спортивного мастерства для их подготовки к чемпионату Европы, если 10 лучших результатов таковы: хiсм : 230, 228, 227, 227, 221, 220, 218, 215, 210, 208 (26).
Решение. Введём данные результаты в программу Microsoft Excel. Если бы они были в хаотическом порядке, то после введения в столбец таблицы их необходимо привести в любой из двух ранжированных видов. Выполняя в этой программе соответствующие действия с учётом формул (3, 4, 6, 7’, 8’, 24), найдём для основной совокупности (26): х=220 см; σ=7,7 см; xmin=208 см; xmax=230 см; n=10; х’=12; v=3,5 %; v’=62 %; U=2,86. Согласно критерию Дэвида – Хартли – Пирсона (26), с уверенностью в 95 % можно считать нормально распределённой и для неё применимы все параметрические методы. Если ориентироваться на v=3,5 %, то эту совокупность следует считать однородной. Но каждому специалисту по прыжкам в высоту ясно, что это не так в связи с разной подготовкой данных прыгунов, т. к. х=230 см соответствует нормативу мастера спорта международного класса, а х=208 см – нормативу кандидата в мастера спорта. Это и подтверждает приведённый коэффициент вариации v’=64 %. Значит, информативность среднего значения х=220 см и однородность всей группы прыгунов неудовлетворительная. Выделим из неё хотя бы удовлетворительно однородную выборку. Для этого в столбец A программы Excel введём данные основной совокупности. В столбце B определим приведённую совокупность, вычитая из каждого Аi xmin=208. Вычислив х’=12,4, примем его за точку деления приведённой совокупности на две части: верхнюю из x’1-x’6 и нижнюю из x’7-x’10. Выделение однородной выборки следует начинать с наиболее однородной части. В данном случае ПКВ верхней части v’=23 %, а ПКВ нижней части v’=96 %. Значит, процесс группировки надо начинать с верхней части. Так как она уже удовлетворительно однородная, то ее объем можно увеличивать за счет следующих данных до тех пор, пока она будет оставаться однородной. Добавив к ней следующее данное x’7=10, получим v’=28 %≤33,3 %. С последующим добавлением x’8=7 получим v’=36 % > 33,3 %, т. е. x8 уже является вариационным арте- фактом для выборки x’1-x’7. Очевидно, что x’9 и x’10 тоже для неё будут артефактами, и процесс увеличения объема выборки заканчивается на x’7=10. Таким образом, из десяти результатов только лучшие семь образуют удовлетворительно однородную совокупность в вариационном интервале [208 см, 230 см] и их САЗ=224 см является удовлетворительно информативным. Так как по условию задачи из основной совокупности нужно выделить выборку результатов с отличной однородностью, то, продолжая процесс группировки с целью выделения из удовлетворительно однородной выборки искомой выборки с отличной однородностью, получим: для лучших четырёх результатов v’4=7 % – отличная однородность, а для лучших пяти результатов v’5=18 % – хорошая однородность. В итоге имеем, что из неоднородной основной совокупности (26) с неинформативным САЗ в вариативном интервале [208, 230] выделены следующие варианты однородных выборок: xj : 230, 228, 227, 227, 221, 220, 218 – (хj=224; σj=4,6; xmin=208; xmax=230; nj=7) с удовлетворительной однородностью и информативностью САЗ, с тремя артефактами: 215, 210, 208; xk : 230, 228, 227, 227 – (хk=228; σk=1,4; xmin=230; xmax=208; nk=4) с отличной однородностью и информативностью САЗ; xl: 230, 228, 227, 227, 221 – (хl=227; σl=3,4; xmin=208; xmax=230; nl=5) с хорошей однородностью и информативностью САЗ. Значит, на подготовку к выступлению на чемпионате Европы одинаково претендуют прыгуны с результатами: 230, 228, 227, 227 см.
При этом по критерию Дэвида – Хартли – Пирсона все полученные однородные выборки отвечают требованию нормальности с доверительной вероятностью в 95 %, т. е. к ним можно применять нормальные параметрические методы.
Заключение . Приведённый коэффициент вариации по сравнению с общим объективнее отражает однородность статистической совокупности и информативность её среднего значения. Для нормальной совокупности с его помощью можно определить, когда она становится неоднородной и её среднему значению доверять не следует. Сравниваемые группы исследуемых можно подвергать одинаковому воздействию только тогда, когда результаты их измерений по рассматриваемым признакам образуют однородные совокупности.
Отсутствие единого подхода к группировке статистических данных приводит к неоднозначным результатам и не позволяет объективно оценить различные её варианты. Во многих случаях исследователи делят массив данных на части субъективно или используют формулу Стерджеса [5], которая учитывает только объём данных без учёта их главной особенности – относительной вариации. Возможно, предложенная в работе четырёхбалльная градация информативности САЗ и подход к выделению однородных выборок, с учётом их основных вариативных интервалов и приведённых коэффициентов вариации, поможет устранить многие проблемы группировки в различных сферах деятельности человека.
Список литературы К оценке однородности количественной статистической совокупности и информативности её среднего значения
- Кобзарь А. И. Прикладная математическая статистика: для инженеров и научных работников. -М.: Физматлит, 2006. -816 с.
- Лемешко Б. Ю., Рогожников А. П. Исследование особенностей и мощности некоторых критериев нормальности//Метрология. -2009. -№ 4. -С. 3-24.
- David H. A., Hartley H. O. and Person E. S. The distribution of the ratio, in a single normal sample, of range to standard deviation//Biometrika. -Vol. 512, -No. 3/4 (Dec., 1964), pp. 484-487.
- crypto.nut2.ru>normal.htmi
- statanaliz.info>metody/gruppirovka. Простые способы группировки данных.


