К оценке погрешности обработки деталей при интеллектуальном управлении станком

Введение. Общеизвестно, что точность обработки является важнейшей характеристикой любого технологического оборудования, в данном случае — металлорежущего станка с ЧПУ. Под точностью обработки понимают степень соответствия рассматриваемых параметров изготовленной детали к их теоретическим номинальным значениям. Как известно, повышение точности изготовления деталей увеличивает срок службы машин и оборудования. При недостаточной точности изготовления составляющих машину частей качество её функционирования будет невысоким и в процессе работы могут возникать существенные динамические нагрузки, которые приводят к ускоренному износу оборудования и его разрушению [1].

Причины возникновения погрешностей обработки на металлорежущих станках связаны с ошибками исполнения основных и вспомогательных движений, выполняемых станком, деформациями и износом узлов станка, используемых приспособлений и инструментов, а также с деформациями обрабатываемых на станках заготовок под действием усилий резания, температурных полей и др.

Существует ряд работ, посвящённых проблеме повышения точности механической обработки на станках. Над данной проблемой работали такие учёные в области технологии машиностроения и металлорежущих станков, как А. А. Маталин, В. Э. Пуш, Д. Н. Решетов, В. Т. Портман, В. А. Ратмиров, К. С. Колев, С. Хуанг, Р. Пигерт и др. Работы этих учёных заложили базу знаний для дальнейшего поиска путей повышения точности обработки на станках с ЧПУ.

Применение систем интеллектуального управления в металлообрабатывающих процессах связано, прежде всего, с тем, что дальнейшее повышение качественных характеристик оборудования невозможно без учёта большого количества факторов, параметров, многие из которых имеют случайный характер [2]. Решение этой задачи может быть найдено лишь при использовании интеллектуальных систем, способных находить решения в недетерминированных ситуациях при наличии стохастических процессов. База знаний такой интеллектуальной системы управления должна содержать в себе сведения обо всех проводимых ранее подобных операциях металлообработки и их результатов, на основе чего она формирует наилучший метод решения поставленной задачи [3-5].

Данная работа посвящена оценке влияния погрешностей технологической системы на погрешность механической обработки. При использовании такой оценки может быть обеспечена воз-

Работа выполнена в рамках инициативной НИР.

можность достижения требуемого качества обработки, в том числе точности размеров и геометрической формы изделия.

Постановка задачи. Выполняется разработка методики аналитического расчёта отклонения траектории режущего инструмента в процессе резания и рассматривается её применение для анализа погрешностей обработки на многооперационных станках при использовании интеллектуальных систем управления. Практическое использование методики проиллюстрировано на основе имитационного моделирования процесса обработки поверхности.

Анализ совокупности составляющих погрешностей. Моделирование позволяет проанализировать то, как именно различные источники погрешностей обрабатывающей системы влияют на неточность готового изделия. Погрешности обработки будем классифицировать как наследуемые и оперативные. В то время как оперативные погрешности могут возникать в процессе обработки, наследуемые, в свою очередь, могут быть сведены к нулю [6].

Следовательно, необходимы модели изменения отдельных погрешностей и их влияния на суммарную погрешность операций механической обработки. Для создания модели используем совокупность (выборку) точек, расположенных на поверхности заготовки (рис. 1).

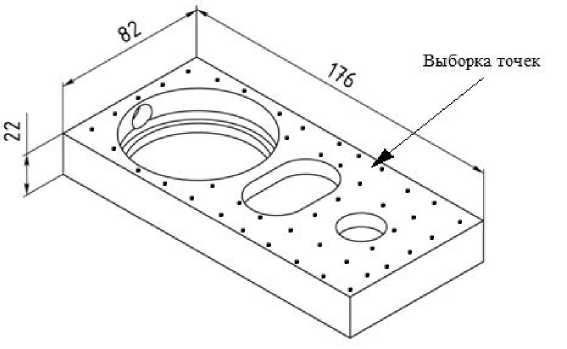
Рис. 1. Обрабатываемая заготовка и выборка точек на поверхности

Чтобы проиллюстрировать метод оценки погрешности, сложность модели погрешностей и количество составляющих погрешностей следует перейти от частных показателей к обобщённым (подвергнуть агрегации).

В качестве проагрегированных погрешностей рассматривается погрешность при закреплении заготовки и износ режущего инструмента [7]. На фрезерном станке система координат станка (СКС) совпадает с системой координат XYZ (рис. 2). Поверхность обрабатываемой детали необходимо установить в начало системы координат детали в качестве точки отсчёта СКС и системы координат заготовки (СКЗ). В ситуации идеального размещения СКС и СКЗ должны совпадать, если совпадают их начала координат и координатные оси. В связи с появлением погрешностей установки и погрешности положения базовой поверхности, СКЗ отклоняется от СКС, образуя систему координат X'YZ' (рис. 2).

Предположим, что верхняя поверхность призматической детали, представленная на рис. 1, фрезеруется на глубину фрезерования tp. Идеальное положение для обработанной плоскости описывается четырёхугольником A-B-C-D (рис. 2).

В связи с погрешностями установки детали, неточностью приспособления, прижимной силой, СКЗ отклоняется от СКС, приводя к отклонению положения обработанной поверхности А-В-С-D. Предположим, что начало координат смещается в точку T_t, повёрнутую вокруг осей X, Y, Z на углы 0_Х, 0_Х, 0_Z соответственно.

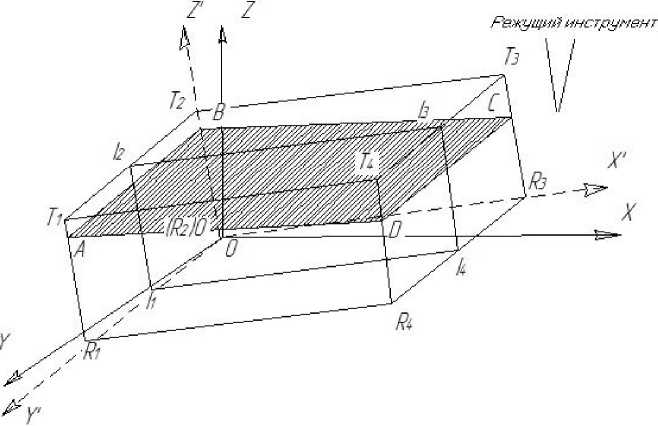
Рис. 2. Система координат X'YZ', вызванная отклонением СКЗ от СКС

Для имитации случайного отклонения (в том числе вращения и смещения) в каждой моделируемой ситуации матрицы случайных значений перемещения и вращения задаются расстояниями а, Ь, св трёх направлениях системы координат. Углы отклонений осей координат 0_Х, 0_У, 0_Z формируются на основе точности установки заготовки. Преобразование координат между СКС и СКЗ может быть достигнуто с помощью следующих выражений:

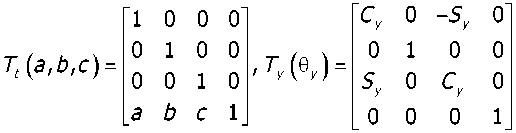
С, = cos9,;

Sj = sin9,;

Представим износ режущего инструмента, как функцию от времени обработки t [8,9]: W = kt, где к— коэффициент износа инструмента во времени, мм/с.

Время на обработку одной детали:

т =

р I// где Vf— подача; Lp — расстояние перемещения инструмента.

Предположим, что инструмент может произвести обработку п поверхностей перед тем, как будет заменён, вследствие износа до максимального допустимого И/тах износа инструмента:

тР-п

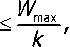
поэтому

^тах _ ^тахУ, к-Т_р kL_p ■

Пусть есть /Vточек обработанной поверхности, равномерно распределённых по направлению оси х. Погрешность обработки, вызванная износом инструмента, в >й точке рассчитывается следующим образом [10]:

• e, = ^Lp • j -k. ^f V_f-N

  
  

Предположим, что инструмент должен переместиться в точку (х, у, z). В связи с погрешностью режущего инструмента, z-координатой этой точки может быть любое случайное значение в диапазоне [z- e_m, z + е_т]. Предположим, что эти случайные погрешности обработки подчиняются нормальному распределению со средним значением в диапазоне от 0 до Зо, равным е_т, т. е.:

f^m) = ^=e

Р=(А-РмУ обозначает множество точек /V выборки, в которой р, = (х,, у_к z) и / = 1.../V. В СКС z-координату реального пути инструмента при отсутствии других погрешностей, за исключением погрешности отклонения инструмента, вводят, обозначая как Zoi.

z_0/ = Н-а_р;(х₁₍у^е6(х,у) = 0.

Z-координата точки /с ошибкой при износе инструмента: z«= zOi+eti(t) = H-ap+eti(ty если погрешность РИ вызвана неточностью установки инструмента на станок: zn = ^о, + eft (t) + emi ^ = Н-ар + eti (f) + emi ^ty, в общем случае, когда учитываются погрешности некоторого числа М компонентов, связанные с процессом обработки или износом режущего инструмента, они могут быть выражены, как:

Преобразованием этих точек из СКС в СКЗ, можно получить функцию точности путём сравнения z-координат этих точек (z_r) с z-координатами точек, расположенных на требуемой поверхности. Матрицы T_t, Т_х, Ту, Т, могут быть вычислены из выражения (1).

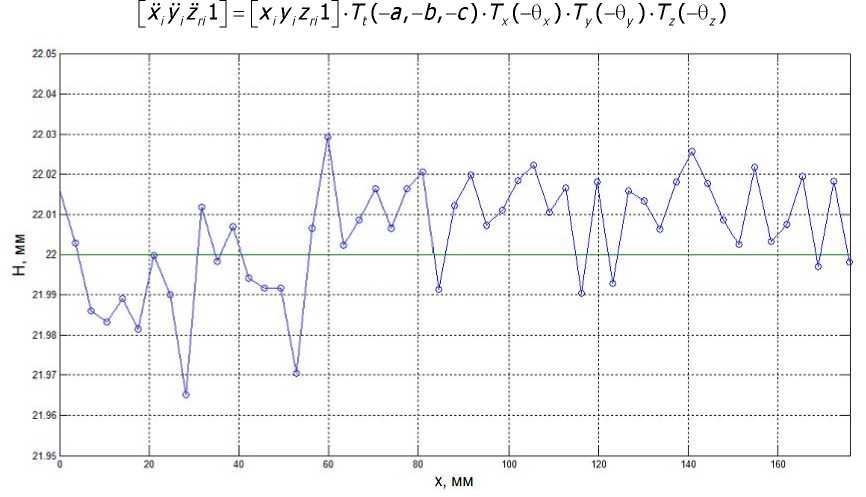
Рис. 3. Фактическая траектория инструмента с учётом его износа и погрешностей обработки

Алгоритм работы программы заключается в следующем:

• 1.    Производится выборка точек обрабатываемой поверхности.

• 2.    На основе исходных данных определяются оперативные погрешности (в данном случае погрешность износа) и наследуемые погрешности в каждой точке.

• 3.    Производится расчёт фактических координат каждой точки с учётом матриц сдвига и

• поворота, полученных на основе исходных данных.

• 4.    Полученные координаты точек используются для построения графика, отображающего реальную обработанную поверхность, который и является результатом работы программы.

• 5.    Полученная функция распределения Z-координаты реального пути режущего инструмента, отражает вероятность попадания значения Zb определённый диапазон.

Из рис. 3 видно, что разброс значений Z-координаты реального пути режущего инструмента не превышает 0,04 мм, что является допустимым в условиях реального производства.

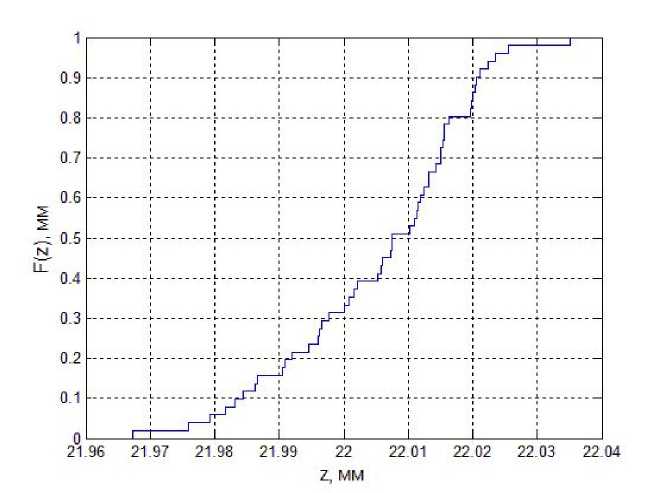
Рис. 4. Функция распределения Z-координаты фактической траектории режущего инструмента

Заключение. Предлагаемый в работе метод основан на анализе влияния отдельных погрешностей на суммарную в процессе механической обработки. В работе использован метод аналитического расчёта отклонения траектории режущего инструмента и рассмотрено его применение при оценке и анализе погрешностей обработки деталей на многооперационных станках. Проиллюстрировано практическое использование метода, приведён пример построения фактической траектории режущего инструмента с учётом его износа и погрешностей обработки. Представленная методика позволяет оценивать влияние погрешностей на процесс обработки и обеспечивает возможность предварительного контроля допуска для обрабатываемых поверхностей.