К одной задаче Белоконя А. В

Введение. Контактные задачи о взаимодействии жесткого бандажа с бесконечным сплошным упругим цилиндром и о нормальном контакте жесткого вкладыша с поверхностью цилиндрической шахты в упругом пространстве рассматривались в работах [1–4]. При этом в сингулярном асимптотическом методе использовалась аппроксимация символа ядра интегрального уравнения в виде суммы двух легко факторизуемых функций, что позволяет найти только приближенное решение уравнения Винера-Хопфа [2]. Позже для этих же задач была предложена аппроксимация символа ядра одной легко факторизуемой функцией [5,6], что позволило существенно облегчить применение сингулярного асимптотического метода, который получил широкое распространение при решении задач со смешанными граничными условиями [7,8]. Анализируя научное наследие профессора А. В. Белоконя [9], сталкиваешься с еще одной интересной задачей, рассмотренной им в начале 70-х годов прошлого века. Это задача кручения жестким вкладышем полого цилиндра, которую тогда удалось эффективно решить лишь для толстостенного цилиндра [3, с. 230]. Цель настоящего исследования — получить решение этой задачи для тонкостенного цилиндра на основе сингулярного асимптотического метода и новой эффективной аппроксимации символа ядра интегрального уравнения.

Материалы и методы. В цилиндрических координатах рассмотрим контактную задачу кручения полого линейно-упругого цилиндра, внутренний радиус которого равен R, а внешний R1. Внешняя поверхность цилиндра жестко закреплена. Внутрь цилиндра помещен жесткий цилиндрический вкладыш длины 2a, к которому приложен крутящий момент M. Под действием этого момента упругий материал цилиндра в области контакта испытывает угловое перемещение иф=-е. Материал цилиндра характеризуется модулем сдвига G. При заданных величинах R, R 1, a, е требуется определить контактное напряжение p(z) в области контакта. Затем может быть определен момент M. При по- мощи метода интегрального преобразования Фурье задача сводится к следующему интегральному уравнению (|х| < a ) [3]:

а          x - z ।

J p ( z ) K II dz = n G e ,   K ( t ) = J L ( u )cos utdu ,

- a        V R J                      0

где символ ядра имеет вид

L ( u ) =

1 -to 1 ( u ) to ( a u )

uK ^{- 1} ( u )[ K ( u ) + I_o ( u ) to ( a u )] + 2[1 - to^{- 1} ( u ) to ( a u )]

to( u) =

K 1 ( u ) 1 1 ( u ),

a = R > 1.

R

Здесь I n ( и ), K n ( и ) — модифицированные функции Бесселя [10]. Безразмерный параметр а характеризует толщину стенок цилиндра. При а— » функция L ( и ) вида (2) стремится к функции

L о ( u ) =

uK - ¹ ( u ) K _o ( u ) + 2,

соответствующей случаю кручения пространства с цилиндрической шахтой.

Ранее было установлено, что при а>3 и и >0 функция L _o ( u ) вида (3) достаточно хорошо аппроксимирует функцию L ( u ) и было получено полное решение уравнения (1) с символом ядра (3) [3]. Отметим, что наибольшее отличие этих функций наблюдается в нуле, где

L (0) = A = ¹ - Т1Г,   L о (О) = 1.

2  2 а           2

В бесконечности функция (2) имеет асимптотику:

1     3   , f 1 )

L ( u ) =---г^- + o      , u —У +^ .

2           2

u 2 u    V u J

Введем безразмерные обозначения z' = z,

a

x '= x , p 'И = £ ( z ), aG

- е 1 R е' =  , Х= .

a

a

Штрихи далее будем опускать. Параметр X характеризует относительную ширину области контакта. В обозначениях (6) уравнение (1) примет вид

J p ( z ) K | ^-—z | dz = ns .

- i         v X J

Для решения уравнения (7) применим сингулярный асимптотический метод [5,6], эффективный при достаточно малых значениях X .

Результаты исследования. Получение решения задачи основано на сведении уравнения (7) к интегральному

уравнению Винера - Хопфа, при решении которого используем новую аппроксимацию

L ( u ) ® L , ( и ) =

V и ² + B ²     (      3     ) и ² + A’ G ²

—---— exp--      —---—, u + C     V 2 Vи 2 + E2 J u + G

при условиях

B

_C 2 exp

3 ) ,

- — I A 2 = A, E = 10.

2 E J ⁴¹

Аппроксимация (8), (9) учитывает поведение L ( u ) в нуле и бесконечности, см. формулы (4), (5). Кроме того, функция (8) легко факторизуема. В табл. 1 для разных а даны значения параметров аппроксимации (8) и ее относительная погрешность 9 (в процентах) при и > 0. Значения параметра C определялись из условия (9). Значение а= » соответствует аппроксимации предельной функции (3).

При проведении расчетов параметров аппроксимации использовался метод Монте-Карло.

Таблица 1

Table 1 Параметры аппроксимации

Approximation parameters

а	A 0	B	G	9	а	A 0	B	G	9
∞	1,970	0,8872	0,8447	2,0	1,07	0,4068	4,001	8,696	1,07
3	0,4649	5,651	4,674	0,5	1,06	0,1582	6,088	10,25	4
2	0,8586	1,150	3,340	0,5	1,05	1,251	5,091	4,580	4
1,5	2,192	4,183	3,631	0,3	1,04	1,448	5,002	4,924	4
1,1	3,165	6,887	8,878	2	1,03	1,400	6,991	6,876	4,5
1,09	1,269	6,582	10,09	3	1,02	2,082	5,909	7,875	5
1,08	2,037	6,583	9,164	3,5	1,01	2,715	6,507	9,500	5,5

Значение E специально выбрано большим (см. формулу (9)), поскольку в процессе получения сингулярного асимптотического решения используется еще одна аппроксимация в полуплоскости Re s >  0 :

^exP⁽ y ^{( s})) ® ¹ + y ^{( s}) , (10)

У ^{( s}) =

3      , s + V s ² - E ²

ln

2n^s ² - E ^{2        E}

При выбранном значении E относительная погрешность аппроксимации (10) при действительных 5 > 0 не превышает 0,3 %.

В результате применения метода Винера - Хопфа главный член асимптотического решения интегрального уравнения (7) при малых X можно построить в форме

Р ^{( x} ) = Г

X

V

1 + x I

X J

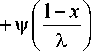
A

(| x | < 1),  (11)

W ( s ) + 1 ( s )            3 s

V ⁽ s ) = A- ,   I ⁽ s ) = X“J W ⁽ s ^{-T )} K o ^{( E t )} d т ,

V A            2п о exp(-Bs)  | C 1 - A J

W ( s ) = — —  + -= + —20 erf (V Bs ) +

V n s    V V b   A 0 J

+ (1 A )( A 0 G Q exp( _ AGs )erf(^ в _ A g ) _s ^

A o V B ^_ A 0 G

Здесь erf( x ) ― интеграл вероятностей, На основании формулы (11) можно получить выражение для интегральной характеристики решения (момента M ).

Как показывают расчеты, погрешность асимптотического решения (11) при Х<1 не превышает (6 +9 )%, где 9 ― погрешность аппроксимации (8).

Обсуждение и заключение. Аппроксимация вида (8) пригодна не только для тонкостенного цилиндра для цилиндра любой толщины (при любых значениях параметра а ). Как правило, с уменьшением толщины цилиндра (с уменьшением а ) погрешность 9 возрастает. При значениях а <1,02 цилиндр можно рассматривать не только в рамках теории упругости, но и в рамках теории цилиндрических оболочек (толщина оболочки обычно составляет не более двух процентов радиуса срединной поверхности). Приближенное аналитическое решение (11) можно рекомендовать инженерам для анализа прочностных характеристик деталей цилиндрической формы при кручении жесткой шайбой (вкладышем), когда длина шайбы 2 а превышает внутренний диаметр цилиндра 2 R (при этом Х= R / а <1 ).