К определению формы образующей стенки дозатора устройства для обработки семян защитно-стимулирующими веществами

Известно [1], что при проектировании транспортирующих и дозирующих ёмкостей устройств обработки семян защитно-стимулирующими веществами стремятся образующую стенок последних выполнять в виде линии скольжения дискретных частиц сыпучего тела (потока). Это позволяет устранять в ёмкости застойные зоны, со- здавать «мягкий» режим работы ёмкости и, наконец, получать максимальные расходные её характеристики. Другими словами, стремятся разработать ёмкость для гидравлического вида истечения сыпучего тела. При этом образующая стенки этой ёмкости должна иметь вид граничной линии скольжения потока сыпучего тела.

Линии скольжения частиц - это их тора, у которых центр тяжести смещён от- траектории движения в потоке сыпучего материала, находящегося в граничных условиях.

Аналитически определим вид траектории движения реальных частиц сыпучего тела в граничных условиях ёмкости доза- носительно их геометрического центра на величину £ (£ - эксцентриситет).

С этой целью рассмотрим в плоской декартовой системе координат ОХУ (рис. 1) несвободное движение частицы в форме капли массой т .

Рис. 1. К определению линии скольжения (траектории) частиц со смещенным центром тяжести:

O* - геометрический центр частицы; O'B = — - половина частицы;

a - длина всей частицы; A - центр тяжести частицы; £ - величина смещения центра тяжести частицы от её геометрического центра (эксцентриситет)

Движущаяся частица OB находится в сложном движении, состоящем из прямолинейного переносного и относительного вращательного. Последнее возникает в результате того, что частица со смещённым центром тяжести движется в потоке сыпучего тела, вызывающем поворот частицы вокруг её геометрического центра O .

Используя теорему о кинетическом моменте, напишем дифференциальное уравнение вращения частицы O B вокруг точки O .

d ξi и „ з    тт,             (1)

dt ²

где  Iu - момент инерции частицы отно сительно её точки вращения O ;

L_m - главный момент всех внешних сил (активных и реактивных связей) относительно этой же точки вращения;

^ i - угол ориентации частицы при её повороте относительно оси OY ;

to - частота вращения частицы (поворота частицы).

Имея в виду, что   I u = т • £ ;

d2ξ  dω

—у- =   i-, а Lm = mgto • sin ^ и до- dt2    dti       m пуская, что в разрыхлённом потоке сыпучего тела реакции связей частицы с соседними по потоку частицами малы по сравнению с гравитационной силой G = mg , получим следующую последовательность решения дифференциального уравнения (1):

и, следовательно,

- 2d^     „      s m • £ -=- = m • £ • g • Sinii;

' gtL ii = 2arctg e 2£  •

d to i-    g • Sin ^ i

dt

;

£

g • Sinii      „ toi =--ti + C1•

£

V )

Частица, перемещаясь к выпускному отверстию дозатора в плоской системе координат, имеет две степени свободы. Для нахождения уравнения её движения достаточно составить уравнение, связывающее ординату Y с действующими на частицу силами. Тогда будем иметь уравнение

При t i = 0 и ^ i = 0 , C = 0 . Тогда

g • ^{Sin i} i ^ i                  t i •

£

d2Y m —у = mg.

dt i ²

Так как d2Yi  dVYi

d i

Учитывая, что to; =---,

,          i     dti , уравнение (1) принимает вид

dt_i ²     d^t Yi

, то

dV

Y^T = g и dt_Yi

d ^ i _g • Sin i

dti

£

. t.

t_i .

V Yi = ^gt i ^{+ C} 3 •

При начальных

условиях t i = 0

V Yi = 0 имеем C 3 = 0 .

Тогда    V_Yi = gt i ;

и

После преобразований имеем:

-^i- =   • ti. dt i

Sin^i   £ или

dY i dt_i

= gt i

и

ln tg ^

V ² )

g •

£

•

t i ²

+ C i .

Y i = gti" + C 4 •

При начальных условиях

Y i = 0 получим C 4 = 0 и

t i = 0

и

r

При t i = 0 , ^ i =

и C 2 = 0

Тогда

ln tg ^

V ² )

i i

П , а ln I tg 5L | = 0

g •

=----•;

£

V

2 )

gt _i

Y 2

.

Подставляя (5) в (3), будем иметь:

ⁱ i = ²arctg e ^£

V )

Из рисунка 1 следует, что

X i = £ • Sin i i , откуда

.

gti tgk = e2£ ,

X ii = arcSin —i- .

V £ )

Подставляя (7) в (6), получим:

или

(8):

X arcSin —i- = 2arctg e

V £ 7

Yi e £ = tg

Yi

£

V 7

X arcSin —L

V £ 7

.

,

Проведём преобразование формулы

Y = In £

tg

( xX arcSin — -----£

.

Тогда окончательно будем иметь:

Yi = £ • ln

tg

f xA arcSin —L

V £ 7

.

Уравнение траектории движения частицы со смещённым центром тяжести представляет собой логарифмическую кривую, описываемую уравнением (9) и представляющую собой линию скольжения в граничном потоке с наименьшим сопротивлением движению (рис. 2).

В уравнении (9) Y i- = H i - текущая высота дозатора; X i = R i - текущий радиус поперечных сечений образующей дозатора относительно оси OY .

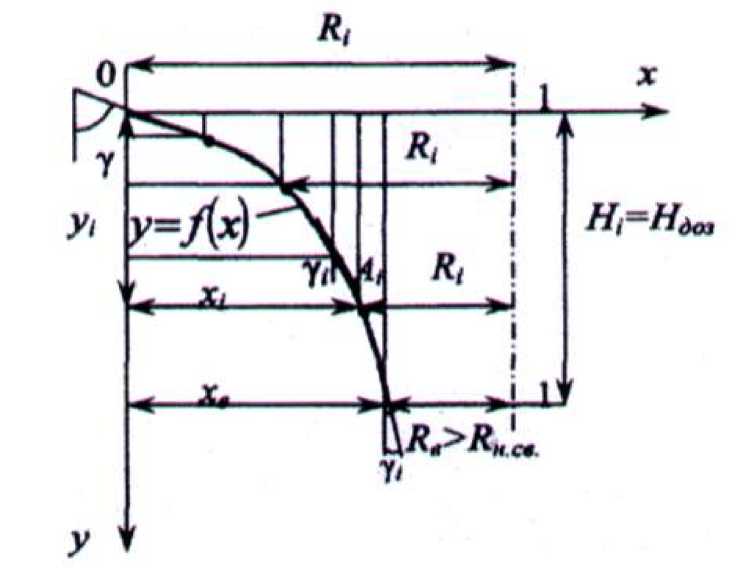
Рис. 2. Траектория движения частицы со смещённым центром тяжести в граничном потоке сыпучего тела

Из теории Л.В. Гячева [2] известно, что образующие стенок ёмкостей (бункеров) описываются зависимостью типа

Hi = 8 ■ ln arcSin Г Ro — Ri) (   8   ) , (10) tg 2 [ i где Ro — Ri = Xi, Ro - входное отверстие дозатора наибольшей пропускной способности.

При этом в таких ёмкостях наблюдается неразрывность (непрерывность) пото- ка сыпучего тела, т.е. расходная характеристика в любом поперечном сечении такой ёмкости (по её высоте Hi ) остаётся постоянной и заметной пульсации потока не наблюдается. Однако ёмкость (дозатор) будет работать только в том случае, если RB > RH св , где Re - рабочий радиус выпускного отверстия дозатора (рис. 2); Rн.св. – наибольший сводообразующий радиус выпускного отверстия дозатора.

На рисунке ось 1 – ось симметрии дозатора. По теории В.А. Богомягких [1], для бункеров и дозаторов указанной формы

R н.св.

d y [ A o ( 2 a i ' П + 3 P ) ' tg ( в + Y ) + 3 P ' Sin2 в • tg a ] 6 p • Sin ( в + ф ) ■ ( 1 + 3 ■ tg a )

где d _y – условный диаметр частицы;

• p - плотность сыпучего тела в ёмкости дозатора;

• П - плотность частицы (семени);

• в - угол укладки частиц в объёме дозатора;

• ф - внешний угол трения частиц;

• A o ,a, 3 - коэффициенты;

Y - угол между касательной к образующей в начале координат O с вертикальной осью дозатора 1 .

Таким образом, для обеспечения «мягкого» режима истечения семян из дозатора при его максимальной производительности необходимо, чтобы образующие его стенок были выполнены по логарифмической кривой.