К определению теплофизических свойств сплава Ti-10V-2Fe-3Al при ВДП

Несмотря на заполненость международного рынка сплавами, такими как Ti–5553(1), Ti–15V–3Al–3Sn–3Cr, сплав Ti–10V–2Fe–3Al до сих пор является ценным конструкционным сплавом, который в большой степени применяют в авиационной промышленности для изготовления деталей шасси. Более того, сплав Ti–10V–2Fe–3Al обладает большей технологической пластичностью и лучшей про-каливаемостью, чем его аналоги [1, 2].

Для получения надежных результатов моделирования и последующего их применения необходимо знание достоверных значе- ний большого спектра свойств используемых материалов в широком диапазоне. В настоящее время в промышленности широко используются быстродействующие ЭВМ для математического моделирования тех или иных технологических процессов [3].

В силу высокой химической активности титановых сплавов измерение теплофизических свойств и их температурных зависимостей при повышенных температурах (выше 700–800 °C), а особенно в жидкой фазе, является в высшей степени сложной задачей [3]. К сожалению, в открытой печати опубликовано ограниченное количество работ, посвя- щенных измерению таких свойств. Экспериментальные же методы, использованные в этих работах для их измерения чрезвычайно сложны и не могут быть применены в условиях заводских лабораторий. Поэтому для решения подобных задач, возникающих в технических приложениях, были разработаны различные экспериментально-теоретические подходы, позволяющие косвенно оценивать неизвестные величины.

Так, в работах [4–6] была предложена экспериментально-теоретическая методика определения теплофизических свойств титановых сплавов в жидкой фазе, основанная на анализе профилей жидкой ванны полностью затвердевших слитков после вакуумного дугового переплава (ВДП). Экспериментальная часть методики позволяет легко оценивать контуры жидкой ванны без использования каких-либо маркеров (например, радиоактивных изотопов); теоретическая часть основана на решении обратной задачи теплопроводности для затвердевающего слитка. Методика была успешно апробирована на модельных сплавах: Ti–3Fe и Ti–5Cr [4–6], и промышленных сплавах: Ti–6Al–4V [5, 6] и ВТ3–1 [6].

В настоящей работе определены некоторые теплофизические характеристики жидкой фазы и параметры граничных условий для ВДП титанового сплава Ti–10V–2Fe–3Al, прямое экспериментальное измерение которых сопряжено с большими трудностями.

Обратная задача теплопроводности

Для математического моделирования затвердевания слитка ВДП необходимо знание многих теплофизических свойств сплава и коэффициентов, входящих в уравнения для граничных условий [7]. Значения некоторых величин либо «ненадежны», либо вообще неизвестны, поэтому для их косвенной оценки предлагается решать обратную задачу теплопроводности [4, 5]. При ее решении одни параметры задаются, а другие – являются искомыми [8]. Определение неизвестных параметров проводится из сравнения расчетных профилей жидкой ванны в различные моменты времени с измеренными экспериментально. Из эксперимента определяется набор измеренных координат zU3M(r,), где индекс k нумерует профили, а ri ‒ заданные радиальные координаты, в которых проводятся измерения, i = 1…N. С целью получения значения z™(ri) были выплавлены два опытных слитка. Характеристики слитков представлены в табл. 1. Расчетный химический состав приведен в табл. 2. Макроструктура слитков А и В показана на рис. 1а и 2а, соответственно. На рис. 1 b и 2 b точками показаны измеренные координаты zкмО^).

Далее, некоторые параметры предполагаются известными (и поэтому их значения фиксированы), а набор параметров b = {b 1 …b M } считается неизвестным. Для определения b проводилось решение обратной задачи теплопроводности, а именно: по распределению температуры в слитке в заданный момент времени t k (эти моменты времени соответствуют измеренным профилям ванны z и^зм (ri)) определялся со-ответствющий набор b k . Для каждого k задача решалась независимо; затем вычислялось усреднением по наборам b = (b 1 +b 2 +…+b k )/K (здесь K ‒ число профилей) [5, 6, 9– 11].

Таблица 1

Экспериментальные слитки

№ слитка	ᴓ, мм	Высота, мм	Ток, кА	Вр. пл., мин	ВДП
А	140	320	2,6	22	1
В	190	260	3,0	22	2

Таблица 2

Химический состав слитков и характеристики фазовой диаграммы

Элемент С0, %		k	μ	m, K/%
Al	3,0	1,13	26,98	9,78
V	10,0	0,95	50,94	‒1,99
Fe	2,0	0,38	55,85	‒22,53
O	0,1	1,33	16,00	41,86
C	0,02	0,50	12,00	‒84,56
N	0,005	1,45	14,01	65,19

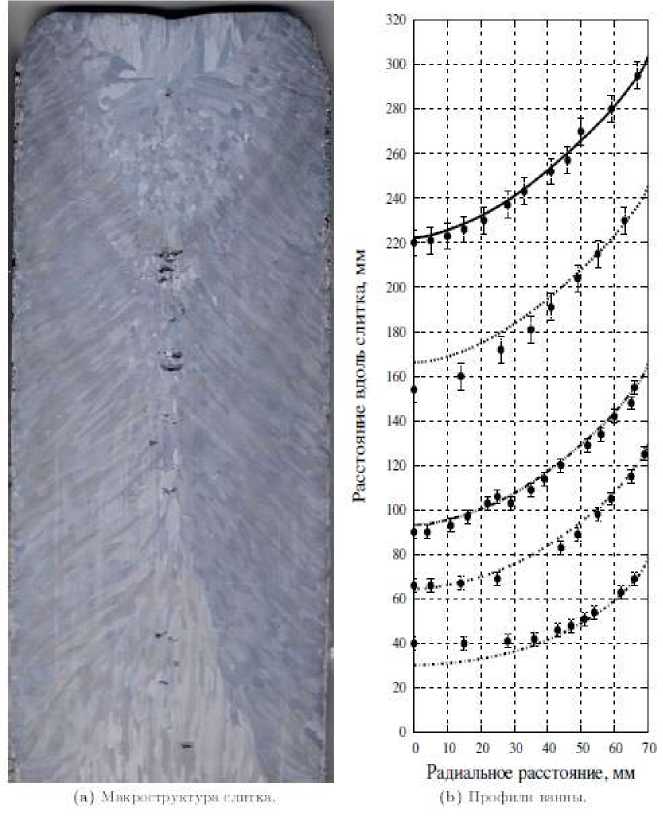
Рис. 1. Сравнение экспериментальных и расчетных профилей ванны (слиток А)

Рис. 2. Сравнение экспериментального и расчетного профилей ванны (слиток В)

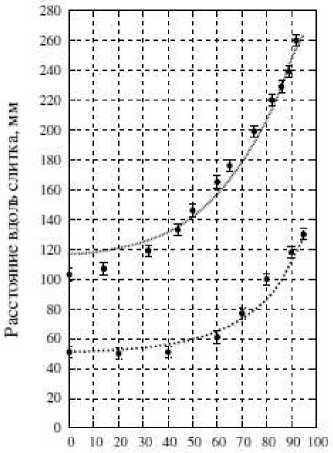
Радиальное расстояние, мм (Ь) П|хк|лг1и валим.

Для решения обратной задачи использовался (для каждого из профилей) следующий алгоритм. Пусть имеется набор измеренных аксиальных координат изотермы ликвидуса (профиля ванны) для заданных радиальных координат z “ ^3M = z £ ^3M(r j ). Используя эти величины, набор из M неизвестных параметров b = {b1…bM} определяется минимизацией функции [8]

R(b)= ^Е^Г — ^СЬ^

। VM ⁽ b m ^_ b m ^{) 2}

⁺ L m = 1   „2    ,                       ⁽¹⁾

°m где zPaC4(b) = zPaC4(ri; b) - рассчитанные аксиальные координаты изотермы ликвидуса в положениях ri с некоторым набором параметров b. Стандартное отклонение σz описывает типичную ошибку при измерениях координат. Изначально она не известна и связана как с ошибкой измерения расстояния, так и с ошибкой самого положения требуемой изотермы, так как точно не известно, какая именно изотерма фиксируется травлением на продольном сечении слитка. При высоких градиентах температуры и малой ширине двухфазной зоны эта ошибка мала и в грубом приближении можно принять az — 3 мм. Стандартные отклонения σm неизвестных параметров bm принимаются равными их типичным интервалам измерения с центральным значением bm. Для минимизации функции R(b) необходимо обеспечить выполнение следующего условия (необходимое условие экстремума функции нескольких переменных)

dR(b) ² yN z изм   "Расчлилл . v I

= ^-T 5 1 i=1^(zi   ^-zi   ^(b)) • X i,m ⁺

^Gb m        ° z

+ -²T ^(b m -b m )= 0,               (2)

°m где коэффициенты чувствительности Xi, m определены следующим образом:

5z p ^ac4(b)

" db m

/XXk. b._ri + 8b m ™b _M )- z ^paC4 (b ! ^b m -b _M ) z-x

, ⁽³⁾

где δb m ‒ малая добавка к параметру b m .

Для определения набора параметров b, минимизирующих R(b), используется итерационный Maximux A Posteriori (MAP) алгоритм [8]. В этом алгоритме координаты, вычисленные на итерационном шаге ν + 1, линеаризуются через координаты на предыдущем шаге ν как zрасч(b(v+1)) — zрасч (b(v)) +

+ Z m=1 X i,m 'Ab m .                  (4)

Набор инкрементов Δb = {Δb 1 …Δb M } искомых параметров на каждой итерации может быть найден решением системы линейных уравнений (которая получается подстановкой разложения (4) в условиях минимизации (2) при b = b^(v+1))

Z M=1 A m,s -^b_s=f m ,                (5)

где

Am^= ^"^.щ-Х^         (6)

°z fm = ^^Г^"^ ))X °z b (v)-b°

• xx .m      ^{b m b m} .                     (7)

° m

Обратный МАР метод (уравнений (5)–(7)) может быть вставлен прямо в программу расчета температурного поля, которая вычисляет zpac4(b).

Итерационная процедура включает следующие шаги:

• 1.    В начале итераций (ν = 0) компоненты «вектора» b инициализируются некоторыми начальными величинами

• 2.    Вычисляются координаты z p ^ac4(b^(v) ).

• 3.    Каждый параметр b j^) изменяется на величину δb m .

• 4.    Вычисляются координаты z p ^ac4(b^(v) + + 5b).

• 5.    По формуле (3) вычисляются коэффициенты чувствительности.

• 6.    Решается система линейных уравнений (5) размерности M х M относительно инкрементов Δb m .

• 7.    Если | △ b_m/b m ⁾| < £_m ~ 10^-3, то вычисления завершаются и полагается b = b(ν). В ином случае вычисляются новые значения искомых параметров b m ⁺¹⁾ = b m) + ^b_m и итерации продолжаются возвращением на шаг 2 с заменой (ν + 1) → ν.

b^(v = ⁰⁾ = {b m ;m = 1 -M}.

Заметим, что в пределах каждой итерации необходимо решить M + 1 раз прямую задачу с помощью программы моделирования процесса затвердевания. Это, естественно, занимает достаточно много процессорного времени в случае большого числа определяемых параметров и/или медленной сходимости метода (например, при сильной нелинейности зависимости от параметров). Однако наш предыдущий опыт показывает, что при небольшом числе параметров метод сходится достаточно быстро.

Определение характеристик сплава

Определение теплофизических свойств сплавов, необходимых для проведения численных расчетов, выбиралось следующим об- разом.

В качестве заданных параметров были использованы значения коэффициента теплопроводности и удельной теплоемкости в интервале температур 20‒1300 °C из базы данных программы JMatPro, рассчитанные для химического состава из табл. 2. Плотность, теплота фазового превращения, динамическая вязкость и электропроводность были взяты из работы [12].

Искомыми параметрами являлись: тепло- проводность и теплоемкость при температурах солидуса и ликвидуса, коэффициент теплоотдачи от слитка к изложнице и коэффициенты относительного вклада теплоотвода излучением для поддона и изложницы. Уравнения, определяющие физику процесса и тепловые граничные условия, подробно описаны в работе [7]. В качестве начального приближения для неизвестных параметров были взяты соответствующие величины для сплава BT3-1 [5].

Сравнение результатов расчета температуры ликвидуса и солидуса с помощью программы JMatPro с достаточно надежными экспериментальными данными показало большое расхождение, поэтому эти температуры были вычислены отдельно, как это опи- сано ниже.

Так как на сегодня нет данных по равновесной фазовой диаграмме сплава Ti–10V– 2Fe–3Al, поэтому для описания многокомпо- нентного сплава мы используем модель независимых компонент (линейная модель), т. е.

температура равновесного ликвидуса определяется как [13].

ТL= Т m + ∑jm j ∙С0 ,j , (8) где T m ‒ температура плавления чистого растворителя (для титана T_m = 1941 K); m j ‒ наклон линии ликвидуса для j-го компонента сплава; C 0, j ‒ номинальный состав j-го компонента в сплаве.

Вычисление параметров mj из бинарных фазовых диаграмм состояния при малых значениях C0, j представляет значительные трудности, поэтому мы для вычисления mj воспользовались уравнением теории разбавлен- ных растворов

m=

RT² 1-kj ^∆H∙       ,

где R = 8,315 Дж∙моль ‒1 ∙K ‒1 (универсальная газовая постоянная), kj ‒ равновесный коэффициент распределения, μj – молекулярный вес, ΔH = ‒15,1 кДж∙моль‒1 ‒ теплота плавления чистого титана. Значения коэффициентов распределения были взяты из работ [14, 15]. Значение kc = 0,50 оценено по бинарной диаграмме. В табл. 2 приведены некоторые характеристики фазовой диаграммы сплава Ti–10V–2Fe– 3Al, необходимые для дальнейших вычислений. Кроме того, мы вычислили «температуру ликвации» (т. е. эффективный интервал кристаллизации) согласно уравнению

∆Т 0 = -∑jmj ∙С0,j∙ ' . (10)

Для значений, приведенных в табл. 2, температура ликвидуса T L = 1636 °C, а интервал кристаллизации составляет ΔT 0 = 72 °C, т. е. температура солидуса T s = T L ‒ ΔT 0 = 1564°C. Такие «температуры ликвации» характерны для сплавов BT3–1, Ti–6242 и Ti–6246.

Результаты исследования

Слиток А

На рис. 3 представлена экспериментальная зависимость глубины жидкой ванны от высоты наплавленного слитка (точки) для слитка однократного переплава А. Зa профиль ванны принимался соответствующий профиль изотермы ликвидуса, представленного на рис. 1 b.

На рис. 2 а показана макроструктура слитка, на рис. 2 b показано сравнение расчетных профилей изотермы ликвидуса и экспериментальных профилей затвердевания. Видно, что полученные значения теплофизических свойств и параметров граничных условий удовлетворительно описывают динамику изменения профиля ванны в течение режима переплава.

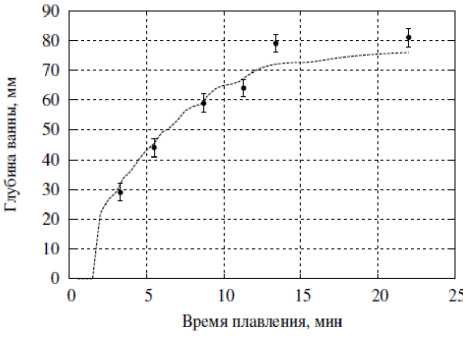
Рис. 3. Глубина жидкой ванны в зависимости от времени плавления: слиток А; точки ‒ эксперимент, кривые ‒ расчет

Слиток В

На рис. 2 а показана макроструктура слитка двойного переплава В. На рис. 2 b показано сравнение расчетного профиля изотермы ликвидуса и экспериментального профиля затвердевания последней лунки перед выключением тока печи. Видно, что полученные значения теплофизических свойств и параметров граничных условий и в данном случае удовлетворительно описывают профиль ванны.

Заключение

В представленной работе методом решения обратной задачи теплопроводности произведено определение теплофизических характеристик сплава Ti–10V–2Fe–3Al ‒ теплопроводности и удельной теплоемкости при температурах солидуса и ликвидуса и параметров граничных условий ‒ коэффициента теплоотдачи от слитка к изложнице и коэффициентов относительного вклада теплоотвода излучением для поддона и изложницы.

Найденные значения параметров позволяют удовлетворительно описать изменение профиля жидкой ванны при наплавлении слитка во время ВДП для различных условий процесса (диаметр изложницы и сила тока дуги).