К параметризации многослойной оболочечной области трехмерного пространства

The new parametrizing of a multilayered shell's field of the three-dimensional space is considering, as well as the presentation of unit tensor of two rank and linkages between the different families of the Christoffel symbols are given in this work.

Благодаря применению нескольких базовых поверхностей при параметризации оболочечной области трехмерного пространства точнее описывается изменение по толщине напряженно-деформированного состояния оболочечной конструкции. Поэтому преимущество применения такой параметризации по сравнению с классической для многослойных оболочечных конструкций, в том числе и для толстых оболочек, несомненно. Причем, если при рассмотрении многослойных оболочечных конструкций в качестве базовых применяются лицевые поверхности слоев, то это дает возможность более реально учитывать характер межслойных контактов. В связи с вышесказанным ниже приводится общее исследование предлагаемой параметризации, предполагающее ее дальнейшее применение в построении соответствующей теории многослойных оболочек.

Рассмотрим многослойную оболочечную область пространства, состоящую не более чем из счетного числа слоев. Пусть, слои пронумерованы по возрастанию, то есть, если, например, а - номер какого-нибудь слоя, то номером предыдущего слоя будет а -1, а номером последующего - а +1. Каждый слой имеет две лицевые поверхности. Лицевую поверхность а слоя, находящуюся со стороны предыдущего а -1 слоя, назовем внутренней базовой поверхностью и обозначим через g , а лицевую поверхность а слоя, находящуюся со стороны последующего а + 1 слоя, назовем внешней базовой поверхностью и обозначим через ^.

Радиус-вектор произвольной точки любого а слоя задается соотношением

г(х¹, X- , х³) = ^г\х’, х²) + х³ h(x^], х²) = (1 - х³)^г\х’, х²) + х^{3 (}г\х*, х²), V а (1), где векторные соотношения

(-) ("), 1 2х (+) (+1 1 2х w

Г = Г (х ,х ), г = г (х ,х ), М а

(-) (+)

задают базовые поверхности S и S соответственно.

Вектор

h(x’,x2) = ^r\x*,x2)-^r^(x',x2), Va, отображающий внутреннюю базовую поверхность S на внешнюю 5 , вообще говоря, не является перпендикулярным к базовым поверхностям. Причем конец h(x’,x2) является началом h(x’ ,х2) для любого а

Таким образом, исходя из вышесказанного имеем1

г (х’.х²) = г (х’,х²) += гдх'.х^-ь 22 Ь = г (х’,х²) +

^а*^{а              а}             v-a '              v-a+1

i (+)

г (х ,х ) = г (х , х )+ /, . г (х ,х )- г (х ,х ) . \fa,o.

На основании (1)

У',х2,х3) = оу(х’,х

2,х3) = h(x’,x2), Vx3e [0,1], Vtz е N, (2)

где N - множество натуральных чисел.

Из (2) можем утверждать, что r^V2) = Г3(х’,х2,х3) = гДх‘,х2) = h(x‘,x2), Va е N. (3)

Дифференцируя (1) по хр, получаем г = г +х3 h — x3)r- + x3 r+.(4)

аР аР а Р х 3 аР ар                      .

Ввиду (3) соотношения (2) и (4) можно представить в виде следующего соотношения:

х„ = г- + х3 h ^ (1 - х3)г- + X3 г*,(5)

а' аР      аг х       аР ар' 1

или коротко

Гт =^гГ^<^Е?’*еЬ+}>.(6)

где введены следующие обозначения:

f^ =VW^ =Г, гТ^е{дА^},*е {-,+}.(7)

Легко усмотреть, что на основании (5) и (7) для g_p* ^и g⁴_p имеем d=^Ts ^{= (1}’^xI)f’^+x’f’'’^eb'^{+) w}

Нетрудно получить выражения и для g _pq . В самом деле, по (6) и (8) имеем

§ „= W = g р* ^ = 0 - *³ Y 8™ ^{+ ?}0 ^ Xg-_р^^gy_qV (X³ У g* е W (9)

Следует заметить, что соотношением (5) в терминах [4,5] S^x -ковариантный базис выражается через S<-> - и &+> -базисы .

Легко найти выражения и для S^ -контравариантного базиса через Sc > - и S^i -базисы. В самом деле, на основании его определения [1-3] и (6) имеем f = урЧрЧч=^Ски^^^                  *£{-,+}, (10)

где lg ^T^rJ-r,; Jg = (r.xr.)r., S' = gg 1, *e{-,+}.     (11)

Нетрудно увидеть, что, вводя обозначения

§^ = ^1- =Y& ^le^kmne_lpqglgl §^Н =г" г^! ^^X^lf^Y *e{-,+), (12)

аналогично (6) для S _g -контравариантного базиса будем иметь представление

*£{-,+}.                     (is)

Теперь, жонглируя индексами, введем еще следующие обозначения: 1р⁹⁼Ь-^ ^Р^е{Р>Р>Р}Л5 е{^лл}, Va,VA         (14)

где а и р - номера двух произвольных слоев. Нетрудно подсчитать, что соотношениями (14) введены 36 обозначений.

Легко усмотреть, что при а- р в формуле (14) содержатся (7), (9) и (12). В самом деле, имеем g?" gB4=bJ9’ ^Ре<Р,Р,РХ^9 ^^ЯлЛХ^а, (15) а аа Р        Р

2 В ранее опубликованных работах вместо основной буквы S использовалась греческая буква ст .

и, жонглируя индексами, очевидно, получим упомянутые выше обозначения и еще g^pq = г^v • г⁹, то есть в этом случае всего 36 обозначений.

Не представляет большого труда на основании (14) показать, что имеют место соотношения g^g^.g^ ^Р^^Р,р/рА^Ч = кЯ,чЛ^ ^пб^рпрД^а^р^б. (16)

(z/7 ^к аЗ ар ”

Согласно (14) и (15) связи между различными семействами базисных векторов представятся в виде г р= g ", г „ = g р ” г й Vp е {р, р, р^, Рп е {и, и, А}, Vа, ^р.

сохраняющие силу при жонглировании немыми и свооодными индексами.

Представление единичного тензора второго ранга. Это представление найти несложно. В самом деле, исходя из обычного представления этого тензора [2,3], на основании (17) и (16) получаем

Как видно из (18), введенные выше величины (14) и (15) представляют компоненты единичного тензора второго ранга в многослойной оболочечной области трехмерного евклидова пространства Следовательно, обобщение на случай «-мерного пространства не представляет большого труда.

Теперь введем следующие определения:

Определение 1. Рассмотренная выше параметризация, характеризующаяся заданием радиус-вектора произвольной точки в виде (1), называется новой параметризацией многослойной оболочечной области.

Определение 3. Компоненты g~”, р е {р,р.р}, nepi,f и получаемые из них жонглированием индексами компоненты называются основными компонентами переноса единичного тензора второго ранга при новой параметризации многослойной оболочечной области.

Легко найти выражения для g aS

К

посредством основных компонентов переноса.

В самом деле, на основании (14) и (17) имеем

Учитывая (8), получаем

a-syMg:

Р 4 рЧ

й л            /1      3 х >   3

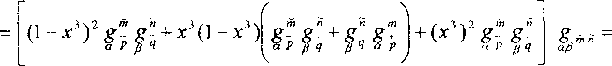
+ О³)² g^ ■ арРЧ

= (1 — х³ )^2,g„_ ч-х³(1 — х³ М g_v + g₊-арРЧ            \аР?Ч арРЧ

Сравнивая (19) и (20), получим искомое представление

g_Pq = ^-^x3y g^+x³0-x³i g аР^Ч              сфРЯ               t^afipq

+ <- + (^)²^„. aP pq          ap pq

«Р р q

Отсюда при a- p получаем (9).

Связи между различными семействами символов Кристоффеля. Для

каждого а слоя ограничимся рассмотрением -5\->-, Sg

- и Sg, -семейств символов

Кристоффеля, для которых введем обозначения Грд -, , Г^ ; Г_и.,. Г^_?, Грд^Г^ соответственно³.

Дифференцируя (17) по х? и пользуясь определением символов Кристоффеля [1-3], получаем

r~~ = 5 г .= d g J г + р-Уг-■ = i 5 я-^я г . + я^^Г* г ‘аИ       ^q^p-J^ РрРр"Ч ^^pPjp" РрГ р^Чр"

Таким образом,

I р

<5 у . ар^р

А 5 рп Ор- \'”Ч" И

У и.р ар Р )Р

где второе равенство получается аналогично первому.

Умножая (21) почленно на Гт= g^r-и x1=gl6rt и учитывая определения символов Кристоффеля [1-3], получим искомые связи. А именно,

3 Классификация символов Кристоффеля подробнее рассмотрена в [4,5].

^=^^4^^                ^.а)           (22)

(/l,tf,7}ej{/),g,/,},{^^ km,M^^m/mA^V^^

Следует заметить, что, когда а = Р, из (22) получаются соотношения, осуществляющие связи между различными семействами символов Кристоффеля рассматриваемого слоя, которые полностью совпадут с аналогичными соотношениями из работ [4,5].