К проблеме анализа и синтеза регуляторов в системах автоматизации металлургических печей

Введение. Актуальность проблемы

Задача качественного построения автоматизированных систем управления технологическими процессами (АСУ ТП) предполагает обязательное решение задачи структурнопараметрического синтеза автоматических регуляторов, задействованных в различных локальных контурах систем. Хорошо известно, что данная проблема совсем не нова, разрабатывается научной общественностью уже более полувека, тем не менее в ее решении еще имеются требующие дальнейшего развития и разработки вопросы. Актуальность и значимость этой проблемы и для настоящего времени отмечается в достаточно представительном списке работ, указанном, например, в [1, 2]. В данных работах предлагаются и анализируются различные способы синтеза систем автоматического регулирования (САР), значительная часть работ посвящена настройке типовых ПИД-регуляторов, их модификациям и вопросам их реализации. Обсуждается и обоснованность применения ПИД-регуляторов, в частности, утверждается, что П-, ПИ- и ПИД- «…алгоритмы были получены чисто эвристическим путем» [3, с. 82] и что «…достаточно убедительное формальное доказательство целесообразности их применения … до сих пор получить не удалось» [3, с. 24]. Весьма важной считается проблема адаптации настроек автоматических регуляторов технологических процессов [4], что со- всем не значимо для САР с объектами типа сервомеханизмов. Утверждается, что «^правильно спроектированная, реализованная и налаженная САР на базе ПИД-регулирования может успешно решать 99 % существующих на предприятиях проблем непрерывного управления технологическими объектами» [5, 6], что «...около 90^95 % регуляторов, находящихся в настоящее время в эксплуатации, используют ПИД алгоритм» [7], что «...ПИД-регуляторы … являются по существу единственными регуляторами, используемыми на практике в системах автоматического управления технологическими процессами» [8]. При этом отмечается, что «…вопреки распространенному представлению ПИД-регуляторы являются далеко не простыми в настройке» [8], поэтому и до сих пор предлагаются новые подходы к решению этой задачи.

Рассматривая проблему автоматизации металлургических печей, прежде всего необходимо отметить, что все многообразие имеющихся здесь локальных каналов управления может быть представлено с помощью следующих типовых передаточных функций [2, 3]:

• ¹    (

• -— ^ехр( ^-т об p );

Tобp kоб

^Т об p + ¹

^ехР^{( -т} об p );

kоб a 2 p 2 + а1 p + 1

^ехР^{( -т} об p ),

где p - комплексная переменная; kоб, Тоб, тоб -соответственно коэффициент передачи, постоянная времени и время запаздывания объекта; а1, а2 - коэффициенты дифференциаль- ного уравнения, описывающего динамические свойства объекта.

К месту заметим, что если по «физике» технологического процесса его передаточная функция имеет несколько иной вид, то используют различные способы приведения математического описания к указанным передаточным функциям. Так, например, по данным проф. А.М. Шубладзе передаточная функция W ( p ) = -—^    при n ^ж превращается в

k звено--ехр(-тp). В работе [9] утвер-

( Tp + 1)

ждается, что данный эффект имеет место уже при n = 8 ^10, а в работе [10] рекомендуется такую замену производить в том случае, если объект управления описывается последовательным соединением двух инерционных звеньев 1-го порядка с существенно различными постоянными времени. На наш взгляд, все это является проявлением того, что называется термином «емкостное запаздывание». При этом параметры указанных передаточных функций определяют по экспериментальным кривым разгона, как правило, графо-аналитическими методами, имеющими достаточно низкую точность оценки. Однако хорошо разработанные и эффективные методы современной теории идентификации в инженерной практике часто не используются.

В учебной литературе по-прежнему базовое место занимает графо-аналитический метод расчета настроек ПИД-регуляторов промышленных объектов, детально разработанный в свое время В.Я. Ротачем [3]. Качество переходных процессов здесь оценивается линейным интегральным критерием, который вообще-то пригоден только для знакопостоянных процессов. Это главный недостаток метода, этот недостаток пытаются компенсировать введением ограничений на запасы устойчивости САР. Утверждается, что это гарантирует достаточно интенсивное затухание переходного процесса, что «…ограничение на запас устойчивости делает процессы регулирования слабоколебательными, площадь под их графиками может быть достаточно точно оценена линейным интегральным критерием» [4]. Тем не менее это требование все-таки не исключает его колебательный характер, поэтому линейный интегральный критерий по-прежнему будет оценивать его качество достаточно приближенно. На наш взгляд, распространенность метода обуславливается тем, что задача минимизации линейного интегрального критерия по параметрам настройки регулятора из ПИД-семейства до конца решается аналитически и получаемые ответы хорошо известны. В самом деле, пусть структурная схема САР имеет вид, указанный на рис. 1.

Здесь ошибка регулирования (рассогласование) вычисляется звеном сравнения системы обычным образом, т. е. по формуле s ( t) = x ^ЗД ( t) - x ( t) , где x ^ЗД ( t ), x ( t ) - соответственно заданное и фактическое значение регулируемого технологического параметра; f ( t ), z ( t ) - возмущающие воздействия;

Рис. 1. Структурная схема типовой системы автоматического регулирования Fig. 1. Block diagram of a typical automatic control system

t - время; W_p ( p ), W₀ 6 ( p ) - соответственно передаточные функции регулятора и объекта управления.

Как известно, линейный интегральный критерий записывается следующим образом:

I — J e ( t ) dt .                                 (1)

Если при этом учесть Лапласово изображение ошибки регулирования to

E ( p ) — J e ( t ) exp( - pt ) dt ,                 (2)

то нетрудно определить, что I = E (0). Следовательно, найдя Лапласово изображение ошибки регулирования и подставив в него вместо комплексной переменной p ноль, получим фор-

I ^{— E} ЗД - E (^{0) —}

1_____ kр

_T  k об

T _И

;

I — E f - E (0) — - ^; k _р

I — E z - e (0) —

T _И

мулу для вычисления линейного критерия.

Ошибка регулирования возникает как при изменении задания x ^ЗД ( t ), так и при измене-

нии возмущений f ( t ), z ( t ). Как это и принято, будем оценивать качество переходных процессов по результатам отработки системой единичных ступенчатых воздействий по всем этим каналам. В этом случае, как это видно из рис. 1, Лапласово изображение ошибки регулирования будет:

при ступенчатом изменении задания

^E ЗД ^{- E ( p} ) p • 1 + W p ( p ) W o6 ( p )

;

при ступенчатом изменении ния f ( t )

возмуще-

E_{f e}( p ) = - 1 •     W ⁰⁶⁽ p )----

F ^- p 1 + W p ( p ) W o6 ( p )

при ступенчатом изменении возмущения z ( t )

1               1

E7_p (p )—---- z E^ p 1 + Wp(p)Wo6(p)

.

Если в САР использовать, например, ПИ-регулятор, то для объектов 2-го и 3-го типов получим:

Здесь T _И – время интегрирования регулятора; k _р – его коэффициент передачи. Как это нетрудно видеть, из всех этих выражений следует, что как при скачкообразном изменении задания, так и независимо от того, по какому каналу действует возмущение (со стороны регулирующего органа или на выходе объекта управления), линейный интегральный критерий будет тем меньше (по модулю в случаях (7) и (8)), чем больше будет отношение коэффициента передачи регулятора ко времени интегрирования k _р T _И. Таким образом, действительно получается весьма «красивый» аналитический результат, причем, подчеркнем, что одни и те же настройки регулятора будут оптимальными как при отработке скачкообразного изменения задания, так и при отработке любого из возмущений, т. е. имеет место инвариантность настроек регулятора относительно точек приложения действующих в САР возмущений. Важно только, чтобы при этом линейный интегральный критерий действительно оценивал качество переходного процесса.

Если же использовать модульный или квадратичный интегральные критерии качества, то требование о должных запасах устойчивости будет излишним. Как это отмечено, например, и в работе [11], экстремумы этих критериев находятся в области устойчивой работы САР. Получение минимальных значений таких критериев уже само по себе является

свидетельством устойчивости САР . Однако, несмотря на это, существует мнение, что ограничение на запас устойчивости все-таки «… должно быть выведено из подынтегральной функции и задано явно» [12].

Недостатки метода расчета настроек ПИД-регуляторов по минимуму линейного интегрального критерия указаны и в статье сотрудников Московского энергетического института [13], как это нам представляется, весьма тесно работавших с В.Я. Ротачем. В [11, 13] напрямую отмечено, что качество переходных процессов в САР, настроенных на минимум линейного интегрального критерия, обычно хуже, чем при настройках на минимум квадратичного критерия.

Вместе с тем, следует отметить, что в обсуждаемой графо-аналитической методике нельзя признать однозначными рекомендации по выбору типа регулятора, отчетливых разъяснений, почему на данном объекте управления разумно применять именно этот регулятор, обычно нет. Очевидно, что все это значительно усложняет задачу синтеза системы.

В литературе широко известны решения задачи синтеза САР, представленные в формульном виде для настроек регуляторов (см., например, [14]), обеспечивающих три типа переходных процессов на типовых металлургических объектах управления. Однако и здесь нет однозначности и отчетливости рекомендаций, нет разъяснений насчет того, как были получены указанные формулы для настроек, следует только предполагать, что это было сделано путем обобщения результатов натурных экспериментов и моделирования.

К месту заметим также и то, что процедура настройки регуляторов остается, как правило, секретом фирм, работающих в данной области [5], поскольку (процитируем еще раз) «…ПИД-регуляторы являются далеко не простыми в настройке» [8]. Об актуальности и значимости этой проблемы свидетельствуют, например, и данные компании Honeywell, которая провела обследование 100 000 контуров регулирования на 350 предприятиях, согласно этим данным 49–63 % САР работает с плохими настройками [15].

В литературе рассматриваются вопросы применения в системах автоматизации технологических, в том числе и металлургических процессов так называемых фази-регуляторов. Привлекательность этой идеи основана на том, что объекты, трудно поддающиеся мате- матическому описанию, довольно часто успешно управляются человеком-оператором, который достаточно не четко объясняет и, конечно, реализует свои действия. Рассматривая перспективность применения таких регуляторов, ограничимся цитированием только того, что высказал в свое время на этот счет проф. В.Я. Ротач «…фази-регуляторы … являются обычными четкими регуляторами. Поскольку квантование только ухудшает качество управления, то … следует считать снятым вопрос о преимуществах таких регуляторов перед традиционными четкими непрерывными регуляторами» [16], что фази-регуляторы являются «…обычными неизвестно зачем усложненными детерминированными регуляторами» [8].

Существенное количество недостатков отмечается и у регуляторов, построенных с помощью нейронных сетей, поэтому в ближайшем будущем не следует ожидать их широкого применения для управления технологическими процессами.

В настоящее время интенсивно используются процедуры синтеза регуляторов методами так называемой H ^∞ -теории [17, 18]. Следует указать, что данная теория является развитием тех классических методов анализа и синтеза САР, в которых использовался частотный подход и так называемый показатель колебательности. В литературе отмечается, что H ^∞ -теория хорошо подходит для управления объектами с так называемой частотной неопределенностью, ее применение для теплотехнологических объектов весьма проблематично. При использовании H ^∞ -методов обычно получаются регуляторы достаточно высокого порядка, при этом числовые значения их параметров настройки, как правило, имеют очень большой разброс, т. е. отличаются между собой на много порядков. Кроме того, если незначительно изменить эти параметры, то регуляторы теряют не только оптимальность, но и перестают стабилизировать систему. По мнению проф. А.А. Красовского, это направление вообще-то иллюстрирует оторванность теории от практики [19].

Известен также метод обратной задачи динамики для синтеза систем управления [19, 20], утверждается, что он «…может с успехом применяться в современной прикладной теории управления» [19]. В этом методе ищется желаемое дифференциальное уравнение для ошибки регулирования. Как это нетрудно видеть, данный метод в целом следует считать несколько иным представлением метода желаемой передаточной функции.

Для повышения качества регулирования в работе [21] предлагается использовать в структуре САР два различных регулятора: один на участке времени, где ошибка регулирования возрастает, а другой – где она уменьшается или, по крайней мере, не растет (или, что то же самое, на разных временных участках – применять разные настройки одного и того же регулятора).

В работе [22] для повышения качества регулирования предлагается использовать дополнительный по отношению к объекту канал, причем его «…передаточная функция … делается такой, что ее сумма с передаточной функцией объекта формирует объект, управление которым … успешно обеспечивается…». Отмечается, что работа является развитием идеи предиктора Смита и, как нам представляется, также и регулятора Ресвика. Идея дополнения объекта моделью или, что практически то же самое, включение этой модели в структуру регулятора – это основная идея предложений и Ресвика, и Смита.

В литературе рассматриваются также и другие модификации упредителя Смита [22]. В работе [23] утверждается, что в системах с регуляторами Ресвика и Смита за счет должной настройки все-таки удается обеспечивать устойчивость и качество управления на объектах с транспортным запаздыванием.

В работе [24] для повышения качества регулирования предлагается использовать принцип управления по прогнозу. Как это показано собственно и в самой работе [24], использование принципа управления по прогнозу равносильно включению в структуру регулятора дополнительных дифференцирующих звеньев, причем повышенного по сравнению с тем, что было в регуляторе порядка. Здесь вполне уместно считать, что П- и ПИ-регуляторы содержат дифференцирующие звенья в степени нуль (нулевого порядка). Такой способ при должной настройке, как это хорошо известно, позволяет заметно улучшить показатели качества регулирования. Поэтому принцип управления по прогнозу, по большому счету, нельзя считать принципиально новым. Скорее всего, это несколько иное представление давно известного способа решения задачи повышения качества автоматического регулирования за счет дифференцирования выхода объекта. Все это достаточно понятно, поскольку производная характеризует и быстроту, и направление (знак) изменения выходного сигнала, что, собственно, и нужно для прогнозирования. При этом следует отметить достаточную проблематичность процедуры дифференцирования реальных сигналов, которые, как известно, содержат не только полезную составляющую, но и помехи. Очевидно, что эта проблема и является причиной появления такого направления исследований, как адаптивное управление с расширенной ошибкой, где не допускается «…измерение производных входного и выходного сигналов».

Известны системы управления, содержащие в своей структуре модели объектов управления [25]. Разумность такого подхода объясняется тем, что выходной сигнал объекта несет в себе информацию о всех входных воздействиях, в том числе и о неконтролируемых. Поэтому по выходному сигналу объекта, управляющим и контролируемым возмущающим воздействиям и моделям каналов, по которым они действуют на выход, можно оценить влияние неконтролируемых возмущений и компенсировать их. Регулятор Ресвика и предиктор Смита, как это нетрудно видеть, следует отнести вообще-то к данному классу систем управления с моделью.

Дальнейшим развитием данного принципа управления является использование моделей для прогнозирования поведения объекта – Model Predictive Control (MPC). Здесь с помощью модели для текущего состояния объекта отыскивается управление, обеспечивающее его оптимальное поведение на некотором будущем отрезке времени (горизонте прогноза). Далее это управление реализуется только на небольшой части горизонта прогноза и измерением определяется фактическое состояние объекта. Начало горизонта прогноза смещается в эту фактическую точку, и вновь вся процедура повторяется. Ввиду малости отрезка реализации считается, что модель объекта может быть достаточно простой, но, конечно, удовлетворительно настроенной на данном временном участке. Как это нам представляется, управление по прогнозу, предложенное в работе [24], можно считать неким упрощенным вариантом применения MPC-принципа.

В целом по вопросу управления с прогнозом важно отметить следующее. Простая обратная связь, доставляющая информацию о текущем состоянии объекта управления, в некоторых случаях оказывается недостаточно эффективной. Объясняется это тем, что за время сбора и переработки информации и реализации управляющих воздействий объект может так изменить свое состояние, что сигналы обратной связи оказываются существенно запаздывающими и практически не характеризующими его текущее состояние. В такой ситуации, очевидно, необходимо прогнозирование состояния объекта, обеспечивающее опережение момента формирования управлений. Обычно все это называется дополненной обратной связью: прогнозирование дополняет обычную сигнальную обратную связь. За счет этого удается заметно повысить качество процесса управления.

В настоящее время в литературе рассматриваются также регуляторы с нецелым порядком интегрирования и дифференцирования [26], это так называемые дробно-степенные регуляторы. В принципе такие регуляторы позволяют добиться более высокого качества регулирования, чем обычные контроллеры. Опубликовано большое количество работ, посвящённых синтезу дробных ПИД-регуляторов, как правило, используются частотный и временной подходы к их проектированию [26]. При их реализации в основном применяются целочисленные приближения. Отмечается также, что для развития данного направления необходима разработка эффективных способов как аппаратного, так и численного представления дробных систем. При этом подчеркивается, что преимущества дробных регуляторов могут нивелироваться сложностью процедуры их настройки [26]. В работе [27], например, отмечено, что применение дробных ПИД-регуляторов не всегда оправдано, что метод их синтеза является «…изощренным», что это приводит «…к настолько сложной структуре регулятора, что эта избыточная сложность уже никак не оправдывается». Соизмеримые или даже лучшие результаты по качеству регулирования могут быть получены и с помощью более простых регуляторов.

Таким образом, все вышеизложенное свидетельствует о том, что проблема выбора и настройки регуляторов, несмотря на достаточно длительную историю зарождения и существования, еще далека от своего окончательного решения, требуется найти понятные и отчетливые ответы на еще многие, казалось бы, уже решенные вопросы.

Выбор эталонной передаточной функции САР

В работах [1, 2, 28–30], как нам представляется, удалось получить некоторое достаточно формальное обоснование целесообразности применения ПИД-регуляторов для промышленных и, прежде всего, металлургических объектов управления, описываемых вышеуказанными передаточными функциями. В данных работах использовался метод выбора эталонной передаточной функции замкнутой системы, причем конкретно передаточная функция задавалась в виде

^Wзс ⁽ Р ) =       ^еХР( — ^Т об Р )’

6 p+1

где 6 - некоторая постоянная времени, а параметр т _об приравнивался ко времени запаздывания объекта управления. Обосновывался такой вид эталонной передаточной функции следующим образом.

Очевидно, что идеальной передаточной функцией замкнутой системы по задающему воздействию является передаточная функция вида W ^ ( p )=1 [1, 2]. В этом случае САР абсолютно точно отрабатывает задание, а также полностью исключает влияние возмущений на процесс управления [1, 2]. Однако, как это достаточно хорошо известно научной общественности, добиться такой передаточной функции совершенно невозможно. Есть смысл попытаться за счет выбора регулятора получить такую передаточную функцию замкнутой системы, которая в определенной мере будет близка к идеальной. Нетрудно видеть, что при малом значении параметра 6 следующие передаточные функции близки к 1 : —¹— , e ^{6 Р} , причем при 6^ 0 предел этих 6 p + 1 передаточных функций будет точно равен 1 . Кроме того, —¹— ® e ^{6 Р} , т. е. данные пере- 6 p + 1

даточные функции приближенно равноценны. Отметим также, что по данным работы [12] система с передаточной функцией —-— яв-6 p+1 ляется оптимальной по робастности и точности. К месту заметим, что в этой работе приводятся следующие значимые для рассматриваемой проблемы данные: «…чем ближе к отрицательной вещественной полуоси располагаются корни характеристического уравне- ния системы», «…тем большую робастность имеет система» и что «…если все полюсы системы находятся на отрицательной вещественной полуоси, то она» «…обладает» «…наиболее высоким потенциалом по роба- стности», «…из множества чисто инерционных систем наиболее структурно-робастным является простейшее инерционное звено первого порядка». Впрочем, аналогичные сведе- ния имеются и в других источниках.

Кроме того, дополнительным обоснованием для выбора данной передаточной функ- ции в качестве эталона являются следующие соображения.

Известно [20], что достаточно рациональным (вполне предпочтительным) является следующий критерий качества переходных процессов в САР:

дующие рекомендации [1, 2, 28–30]: поскольку длительность переходного процесса в САР с передаточной функцией (14) составляет примерно (3-4) a, поэтому если задано время регулирования tр , то, допуская известный запас, a следует вычислять по соотношению tр a =—-— (5 - 6)

Понятно, что параметр a в этом случае играет роль постоянной времени 9 эталонной передаточной функции САР. Поэтому формулу (15) можно использовать для формализованной процедуры определения параметра 9 , естественно, что при этом следует задавать реально достижимую длительность времени регулирования t _р . При этом необходимо иметь в виду

^

I = J[e² + a ²( — ) ² ] dt , 0           dt

где a2 - некоторый весовой коэффициент.

Известно также [2, 20], что оптимальным

по минимуму этого критерия переходным процессом является экспоненциальный процесс, т. е. процесс вида

s ( 1 ) =s (0) exp( - 1 1 a ), (10)

где e (0) - значение ошибки регулирования в

момент времени 1 = 0.

Если при этом считать, что такой переходный процесс должен иметь место при отработке САР единичного ступенчатого задания x3 (1) = 1( 1), то в этом случае е(0)=1 и выходной сигнал САР будет иметь вид x (1)=1 - exp(-1 / a).                     (11)

В связи с этим Лапласово изображение выходной величины запишется так:

следующее: если канал регулирования достаточно инерционный, то, задавая малые значения параметра 9 (или, что то же самое, малое значение t _р ), получим большие, реально недостижимые значения управляющего воздействия. Следовательно, так поступать нельзя.

Сравнительно недавним подтверждением целесообразности отмеченного выбора передаточной функции САР является и работа [13], в которой, в частности, величина 9 называется «…постоянной времени сглаживателя».

При этом вполне понятно, что с запаздыванием мало что можно сделать, поэтому целесообразно оставить запаздывание объекта управления и в структуре эталонной передаточной функции.

L { x ( 1 )} = X ( p ) =     ¹

p ( a p + 1)

далее, учитывая, что

L { x ³ ( 1 )} = X ³ ( p ) = 1, ^p

Синтез регуляторов металлургических процессов по передаточной функции замкнутой системы

Если исходить из того, что САР в целом

найдем передаточную функцию (эталонной) САР

W ( p ) =

X ( p ) X ³ ( p )

a p + 1

образцовой

Как видно из соотношения (14) и из вы-шеотмеченных соображений, разумно, чтобы САР имела передаточную функцию в виде инерционного звена 1-го порядка.

Для выбора величины a имеются сле-

должна иметь указанную передаточную функцию, то для металлургических объектов первого типа передаточная функция квазиоп-тимального регулятора будет равна (прибли-T женно) W (p)=—об—, т. е. близким к иде-р      Тоб +9

альному является П-регулятор с коэффициен-T том передачи к = —об— . Для объекта второ-р тоб +9

го типа квазиоптимальным будет ПИ-регулятор, его передаточная функция будет иметь вид

W ⁽ p ) =

—^{Т о}б— [1+—]. к об ( т об +9 )^L    Т об p

Передаточная функция регулятора для объекта третьего типа будет такой:

W p ( Р ) =

a 1

k об ^{( т} об ^{+9 )}

п 1    ° 2

[1 +---+— Р ],

a1 p   a1

т. е. целесообразно применение ПИД-регуля- тора.

К месту заметим, что синтез приближенный, а анализировать свойства нужно, конечно, реальной САР, поэтому рассмотрим эту задачу анализа подробнее.

Во-первых, важно заметить, что во всех рассмотренных случаях точное выражение передаточной функции разомкнутой системы ,                              ^еХр( -Т₀ б Р )

будет следующим: W (p) = ———"б' , пор       (9 + Тоб ) Р этому, во-вторых, точное выражение передаточной функции замкнутой САР по задающему воздействию также во всех случаях будет равно Wзс (p) =-----eXp( ТобР)-----. Отсю-

^{( 9+Т} об ) p + е^хР^{( -т} об p ) да следует, что дифференциальное уравнение замкнутой САР также во всех случаях будет иметь вид:

^{( 9+Т} об ) d^t ) + x ⁽ t -Т од ) = X ^{З (} t ^-т об ).   (16)

dt

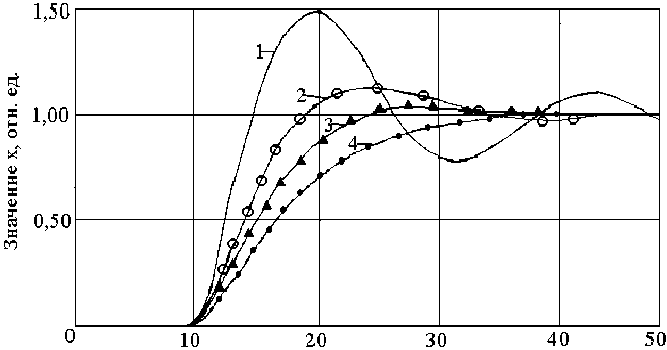
Для оценки характеристик приближенно синтезированной САР выполнили численное интегрирование уравнения (16) для единичного ступенчатого воздействия. Определенная таким образом переходная функция замкнутой системы для т об = 5 с и различных значений параметра 9 приведена на рис. 2: для кривой 1 9=0с; для кривой 2 9=3с; для кривой 3 9=5 с; для кривой 4 9=8 с.

Как видно из рис. 2, во всех случаях САР устойчивая, причем с увеличением параметра 9 колебательность переходной функции уменьшается, переходный процесс в большей степени приобретает апериодический характер (демпфированность САР возрастает), причем при t ^да x ^1, т. е. САР астатическая. Таким образом, можно утверждать, что использование указанного подхода позволяет создавать САР с вполне приемлемыми характеристиками. Кроме того, весьма важным полученным результатом является то, что вполне отчетливо установлено, какой конкретно регулятор рекомендуется применять на конкретном типовом объекте управления в металлургии и каковы должны быть его настройки. В результате задача структурнопараметрического синтеза автоматических регуляторов локальных контуров становится однозначно решаемой как по структуре регуляторов, так и по их настройкам.

Как это известно [25], при использовании приближенного способа синтеза могут возникнуть некоторые проблемы, связанные, например, с появлением каких-то новых, заранее не предполагаемых свойств САР, с их грубостью, с работой в условиях параметрической неопределенности объекта и т. п., поэтому все-таки требуется достаточно детальное исследование этих свойств систем. В работах [28–34] весьма скрупулезно исследовался вопрос о качестве переходных процессов в сконструированных таким способом системах и о грубости их структур и настроек. Во всех случаях установлено, что рассматриваемый метод синтеза локальных САР обес-

Время, с

Рис. 2. Переходные функции САР Fig. 2. Transition functions of ATS

печивает приемлемое качество переходных процессов и достаточный запас устойчивости системы при довольно заметных по размерам вариациях параметров объекта управления и погрешностях задания настроек регулятора.

Сравнение полученных результатовс литературными данными

Часто теплоэнергетические и теплотехнические объекты управления описываются передаточными функциями следующего вида [11]:

^ об = _ kоб _п з • ^ехР^{( -Т} об p )•         (17)

^(Тоб Р + ^{1) 3}

Если задачу выбора и настройки решать предложенным способом, то получается, что на таком объекте управления конкретно нужно применить следующий ПИДД2-регулятор:

37,

WD ( p )=-----об---х р     kоб (тоб +О)

х [1 +

^{3 Т} об Р

+ Т б Р + Т о²б /3 Р ² ].

При этом весьма примечательно, что параметры настройки его ПИ-части, увиденные из формулы (18) и вычисленные для указанных в работе [11] параметров объекта, близки к тем, что указаны в той же работе для ПИ-регулятора, настроенного, например, по модульному критерию качества переходных процессов. Все это также указывает на приемлемость предлагаемого метода синтеза и целесообразность его практического применения.

В работе [13] передаточная функция оптимального регулятора определяется по передаточной функции замкнутой системы вышеуказанного вида, т. е. по W _3C ( p ) = —¹—ехр( -т _об p ).

О p+1

При этом утверждается, что аппроксимация амплитудно-фазовой частотной характеристики (АФЧХ) найденного оптимального регулятора характеристикой ПИД-регулятора обеспечивает минимизацию квадратичного критерия качества переходного процесса. Такое утверждение достаточно удивительно: при решении задачи используется один критерий - W _зс ( p )=—¹—ехр( -т _об p ), а получаем

О p+1

оптимум совсем другого критерия. Причем никаких прямых доказательств этого в [13] не приводится. Кроме того, из данных работы [13] вообще-то следует, что для объекта любого типа субоптимальным будет один и тот же регулятор - это ПИД-регулятор, что тоже никак не аргументировано. Далее в работе используется графо-аналитическая процедура, в настоящее время недостаточно удобная и недостаточно точная, кроме того, нужный диапазон частот отыскивается эвристическим способом. Поэтому утверждение авторов работы [13] о том, что оптимизация настройки регуляторов по квадратичному критерию «...не нашла широкого применения из-за необходимости итерационного поиска оптимальной точки», становится неубедительным преимуществом метода данной работы. Возникает также вопрос: почему бы не решать задачу, используя непосредственно описание САР дифференциальными уравнениями? Всем хорошо известно, что переходные функции (кривые разгона), передаточные функции, АФЧХ и дифференциальные уравнения - это только разные формы представления динамических свойств и характеристик систем и их элементов. Частотные методы разработаны в период, когда не существовало возможности прямого решения проблемы оптимизации настройки с помощью компьютерной математической модели САР и численных методов математического программирования. Частотная методика является графоаналитической, в ней используется ряд допущений, кроме того, как правило, велика трудоемкость используемых процедур. К тому же точность такой настройки контуров регулирования уже нельзя признать вполне приемлемой. В настоящее время предпочтительнее использовать компьютерные алгоритмы параметрической настройки, разработанные на основе достаточно точных математических моделей САР и численных методов оптимизации. Вопросы достижения требуемой точности настройки и уменьшения объема необходимых графических построений и сопутствующих им «ручных» вычислений при этом автоматически снимаются.

Численные процедуры настройки типовых регуляторов

В связи с утверждением работы [13] о том, что оптимизация настройки регуляторов численными методами по квадратичному критерию является якобы затруднительной «.. .из-за необходимости итерационного поиска оптимальной точки», укажем на весьма положительные данные о решениях этой задачи, в частности, в работах [35–37]. В этих работах разработан комплекс программ для численно-

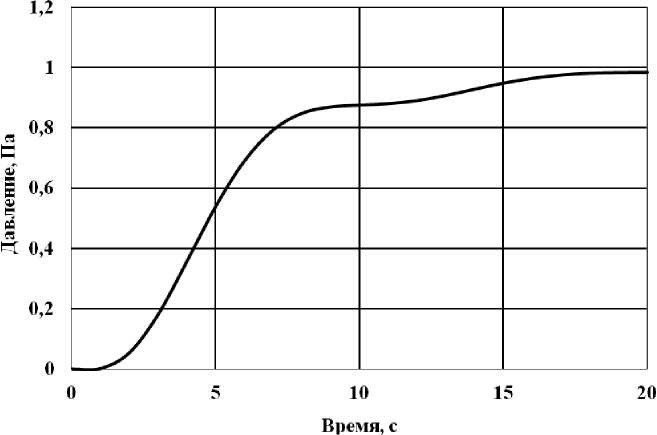
Рис. 3. Переходный процесс в САР давления в рабочем пространстве печи Fig. 3. The transient process in the pressure ATS in the working space of the furnace

го расчета систем автоматического регулирования. Комплекс включает следующие программы:

• 1)    для определения оптимальных значений параметров дифференциального уравнения объекта управления как по экспериментальной кривой разгона, так и по экспериментальной переходной функции работающей САР;

• 2)    для расчета оптимальнах параметров настройки регуляторов из ПИД-семейства как при возмущении по заданию, так и при возмущении по нагрузке (здесь применяется неформализованный выбор типа регулятора из ПИД-семейства);

• 3)    для расчета переходного процесса и показателей его качества в системе автоматического регулирования, включающей типовой регулятор, как при возмущении по заданию, так и при возмущении по нагрузке.

Ниже приведены данные по настройке ПИ-регулятора, работающего с каналом «положение дымового шибера - давление в рабочем пространстве печи». Динамические свойства канала определялись по экспериментальной кривой разгона, объект при этом представлялся передаточной функцией третьего типа, ее параметры, вычисленные с помощью разработанной программы, таковы:

a 2 = 2,366 с²; а 1 =1,750с; т_об = 1,000 с;

к об = 0,800 Па/%ходаИМ.

Здесь ИМ - исполнительный механизм. Оптимальные по квадратичному критерию на- стройки ПИ-регулятора при возмущении по заданию в 1, 00 Па , вычисленные с помощью соответствующей программы, таковы: коэффициент передачи кр = 1,175 % хода ИМ/Па; время интегрирования ТИ = 2,963с. Кривая переходного процесса в настроенной таким образом САР для единичного ступенчатого воздействия приведена на рис. 3.

Следует заметить, давление в рабочем пространстве металлургических, в частности, методических нагревательных печей целесообразно поддерживать на небольшом избыточном уровне в 5,0 = 10,0Па. Это предотвращает как подсосы холодного воздуха в печь, так и существенное выбивание продуктов сгорания из ее рабочего пространства.

В итоге отметим, что комплекс разработанных программ [35–37] значительно облегчает процедуру и повышает точность расчета и может быть использован для настроек промышленных систем автоматического регулирования, в том числе и в металлургии.

Настройка релейных систем

Довольно часто в промышленности, в том числе и в металлургии, значительное количество регулируемых технологических участков оснащены позиционными исполнительными устройствами. Причем замена таких устройств, как правило, не выгодна по тем или иным соображениям. Такая ситуация имеет место, например, при автоматизации электро- печей с контакторными исполнительными устройствами. Вполне понятно, что в этом случае нет другого решения задачи автоматизации, как только применять позиционные Рп-регуляторы [38]. Очевидно, что в этом случае задача синтеза сводится только к выбору параметров настройки позиционных регуляторов. Эта задача детально рассмотрена в работе [38], здесь использовался модельный подход для настройки двухпозиционных и трехпозиционных систем.

Заключение

Рассмотрена проблема выбора и настройки автоматических регуляторов отдельных параметров технологических процессов. Предложен и для типовых металлургических объектов апробирован метод структурнопараметрического синтеза автоматических регуляторов, который дает однозначные отве- ты на следующие вопросы: какой регулятор следует использовать для данного объекта управления и каковы должны быть его параметры настройки. Детальными исследованиями подтверждено, что сконструированные таким образом САР обладают должными запасами устойчивости и приемлемым качеством переходных процессов. Для случая неформализованного выбора типа регулятора (по терминологии [8] экспертного метода выбора структуры регулятора) из ПИД-семейства разработаны процедуры численной оптимизации его настроек по дифференциальному уравнению объекта управления. Приведены результаты настройки ПИ-регулятора давления в рабочем пространстве методической печи. Рассмотрено численное решение задачи моделирования и настройки двухпозиционных и трехпозиционных систем автоматического регулирования.