К проблеме идентификации неизмеряемых параметров распределительной сети по данным АСКУЭ

В последние годы в целях комплексной автоматизации и информатизации распределительных электрических сетей (РЭС) широко используются автоматизированные системы контроля и учета электроэнергии (АСКУЭ), основанные на цифровых технологиях. Функциональная структура этих систем главным образом ориентирована для решения задач, связанных с коммерческим учетом электроэнергии [1]. Как известно, технические и программные средства АСКУЭ имеют возможность дистанционно осуществлять периодический опрос счетчиков электроэнергии, установленных у абонентов сети. При этом непосредственно измеряются и контролируются лишь действующие значения токов и напряжений, определяющих состояния нагрузок (электроприемников) РЭС, а переменные состояния межабонентских участков магистральной линии не доступны для измерения и поэтому не контролируются [2, 3]. В то же время эти переменные (токи и напряжения) распределительной сети, функционирующей в несимметричном режиме [4–6], определяют такие ее важные показатели, как потери мощности и электроэнергии в магистральной линии [7–10]. Использование известных методов и технологий для их идентификации и оперативного мониторинга электрического состояния РЭС [2, 11–15] представляет определенные трудности.

В [3, 16–19] изложены методологические основы оценки неизмеряемых параметров несимметричной трехфазной сети. При этом предварительно решается задача построения математической модели РЭС, которая базируется на комплексном представлении ее переменных, что в определенной степени усложняет проблему нахождения искомых параметров. В данной статье предлагается метод идентификации неизмеряемых параметров межабонентских участков сети, в алгоритме которого непосредственно используются исходные данные АСКУЭ, полученные по каналам связи с абонентских счетчиков электроэнергии, что значительно упрощает процедуру идентификации искомых величин.

Постановка задачи

Рассматривается четырехпроводная РЭС напряжением 0,4 кВ, расчетная схема которой показана на рис. 1.

Обозначения имеют следующий смысл: k,v -индексные переменные, обознача ю щие соответственно номера фаз А, В, С (к = 1,3) и электрических контуров сети (v = 1, и); Ё_ок — ЭДС k-й фазы; U_ok , Т ок = iik — мгновенные синусоидальные напряжения и токи соответственно на входах соответствующих фаз; I_vk , U_vk, Z_vk - синусоидальные мгновенные ток, напряжение и сопротивление нагрузки (электроприемника) с координатой ( v , к); T_vk,z_vk — мгновенный ток и комплексное сопротивление ν -го межабонентского участка (МАУ) k-й фазы; u_vk , H_v - напряжения соответственно на v -м МАУ к-й фазы и нейтрального провода; J_v, z_v - мгновенный ток и комплексное сопротивление ν -го участка нейтрального провода.

Далее предполагается, что выполняются следующие условия:

• 1)    трехфазная сеть является линейной системой;

• 2)    фазные и нейтральные провода сети имеют разные сечения, т. е. комплексные сопротивления

  

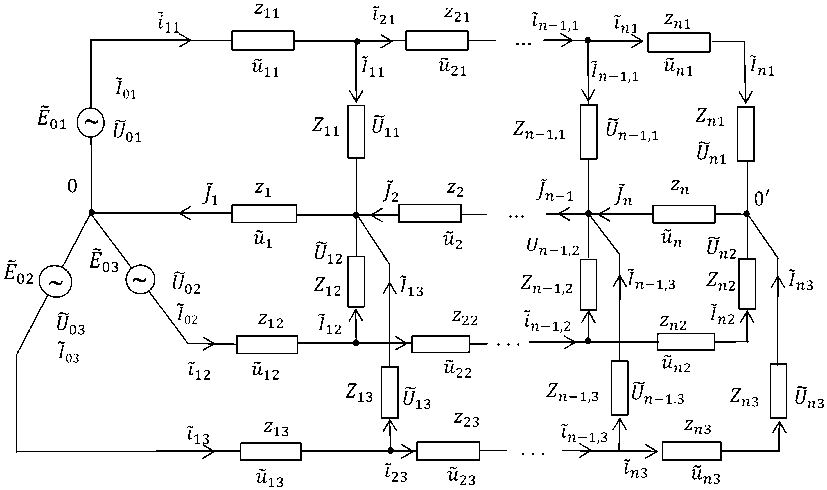
  Рис. 1. Расчетная схема трехфазной сети

  
  

z_vk Ф z_v (к = 1,3, v = 1,n), которые предварительно определяются и записываются в базу данных АСКУЭ;

• 3)    в системе используются технические средства для подавления высших гармонических составляющих токов и напряжений в сети;

• 4)    с абонентских счетчиков электроэнергии (C4_vk) в базу данных АСКУЭ по каналам связи в дискретные моменты времени t Е [t ^ , t ^ ₊₁] с шагом дискретизации ^t ^ = t ^ ₊₁ — t ^ (f = 1,2, ...) поступают следующие данные:

• •    действующие значения токов i_vk и напряжений U_vk на нагрузках сети;

• •    коэффициенты мощности c_vk = cos ф_vk , определяемые фазовыми сдвигами ф_vk между соответствующими напряжениями U_vk и токами I_vk .

Как известно, в современных АСКУЭ межабонентские комплексные токи i_vk, /_v и напряжения i_vk, й ^ не измеряются и не контролируются, что не дает возможность осуществлять оперативный мониторинг электрического состояния РЭС. В то же время на основе метода, основанного на комплексном представлении токов и напряжений в сети, можно их идентифицировать по данным АСКУЭ. При этом мгновенные синусоидальные токи I_vk и напряжения U_vk на нагрузках Z_vk в установившемся режиме представляются в комплексной форме [17, 20]:

i vk = I -k +jI -k =I -k e^jiivk , (1) U -k = U -k +jU -k = U vk e^k, v = 1,n, к = 1,3 , (2) где символы «в» и «м» обозначают вещественные и мнимые части соответствующих комплексных переменных; i_vk, U_vk, ct_vk, ^_vk — модули и фазовые сдвиги этих переменных; j² = —1. При этом

^Cvk = ^P к ^{+ c}vk , ^ vk = ^Pk ⁺ ^ vk ,

Ф vk = ^ vk ^{— c}vk , P k = ^{2(к —} 1) ^ ^/3 , где c_vk, ^_vk - приращения фазовых сдвигов относительно их номинальных значений P k , обусловленные несимметрией токов и напряжений в сети. В случае, когда построена модель нагрузок в форме (1) и (2), межабонентские токи и напряжения можно оценить на основе известных законов электротехники (см. рис. 1):

ivk = ZT=vik = ZT=vUik +jiik) = lvkeJ(^k+».k), (3) ivk = tvkZvk,v = T;^,k = T:3.

jv = ivi + iv2 + iv3, iv = jvZv, v = Vn.     (4)

Анализ соотношений (1)–(4) показывает, что для определения указанных электрических переменных необходимо, чтобы предварительно были определены фазовые сдвиги токов cc_vk и напряжений ^_vk на нагрузках сети, что является отдельной сложной задачей. Дальнейшие исследования показали, что использование подхода, основанного на декомпозиции исходной структуры трехфазной сети, позволяет идентифицировать модули (действующие значения) межабонентских комплексных токов i_vk , j_v и напряжений i_vk, i_v без предварительного построения модели несимметричной распределительной сети на основе комплексного описания ее переменных.

Задача заключается в том, чтобы на основе данных, полученных с абонентских счетчиков электроэнергии, хранящихся в базе данных АСКУЭ, идентифицировать межабонентские действующие токи l_vk, j_v и напряжения u_vk, u_v несимметричной распределительной сети, недоступные для измерения и контроля.

Решение сформулированной выше задачи включает следующие основные этапы:

• 1.    Декомпозиция задачи.

• 2.    Оценка разностей фазовых сдвигов.

• 3.    Идентификация действующих токов и напряжений на участках фазных проводов.

• 4.    Идентификация действующих токов и напряжений на участках нулевого провода.

Декомпозиция задачи . По условиям задачи рассматриваемая трехфазная сеть (см. рис. 1) представляет собой линейную систему. Тогда на основе свойства линейности ее можно расчленить на три подсистемы (составные части), каждая из которых представляет собой соответствующую фазу сети при отключенном состоянии двух других фаз (рис. 2).

Эти подсистемы можно рассматривать как условно автономные структуры, на входах которых действуют ЭДС Ё₀₁ , Ё₀₂ и Ё₀₃ , формируемые источником питания (трансформаторной подстанции) сети. При этом комплексные токи j'_vk и напряжения U^f_vk на нагрузках новых подсистем отличаются от прежних их значений и описываются следующими выражениями:

i’vk = /^е^^ ) ,                  (5)

U'vk = V*^, v = й k = 13, где V_vk и U'_vk - модули соответствующих переменных. При этом их фазовые сдвиги a_vk и ^_vk сохраняются, но их значения неизвестны. Межабонентские токи V_vk также отличаются от их исходных значений, которые можно представить в экспоненциальной форме:

i' vk = l'vk^ei(3*^k+avk), v = Tn, k = 13,       (6)

где l_vk , cc_vk - модуль (действующее значение) и аргумент комплексного тока V_vk соответственно.

Следует отметить, что при такой декомпозиции исходной проблемы значения комплексных сопротивлений сети (Z_vk, z_vk, z_v ) не изменяются. В частности, сопротивления нагрузок можно представить в виде

—      V__              ______ _      -----

Z vk =Z vk e^i(p^ , v = 1,n,k = 1,3,          (7)

где Z_vk , ф_vk - модули и аргументы комплексных сопротивлений Z_vk соответственно, определяемые по исходным данным задачи:

Z vk = ~, V vk = arccos C vk , C vk = cos V vk . (8) ^k

Основная идея декомпозиции исходной структуры трехфазной сети заключается в том, что на ее основе удается найти функциональные связи между фазовыми сдвигами c_vk и ot_vk . В частности, можно численно оценить величины 9_vk , определяющие их разности:

0 v _k = « vk -C v _k,v = TT,k = 13.        (9)

Как видно будет из дальнейшего, знание разностей 9_vk позволяет определить оценки действующих значений l_vk межабонентских токов i_vk, которые недоступны для измерений и в АСКУЭ не контролируются.

Оценка разностей фазовых сдвигов . Предположим, что в момент времени t Е [t ^ , t ^ ₊₁] путем опроса счетчиков электроэнергии в базу данных АСКУЭ поступили данные измерений. Рассмотрим электрические контуры новых подсистем, полученных путем декомпозиции и представленных на рис. 3, где z Vk^B - эквивалентные сопротивления k -й фазы, определяемые выражениями:

z_Vk ^B =^, v = 1, n, к = 1,3.

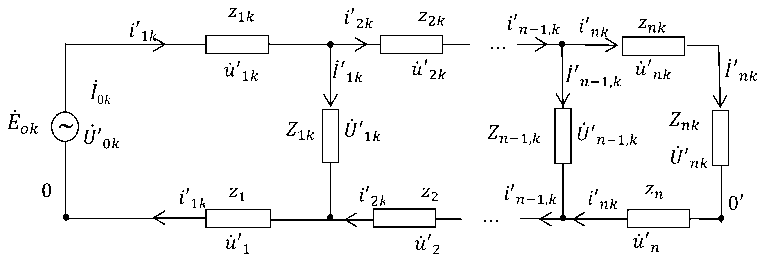
Рис. 2. Структура k -й подсистемы распределительной сети

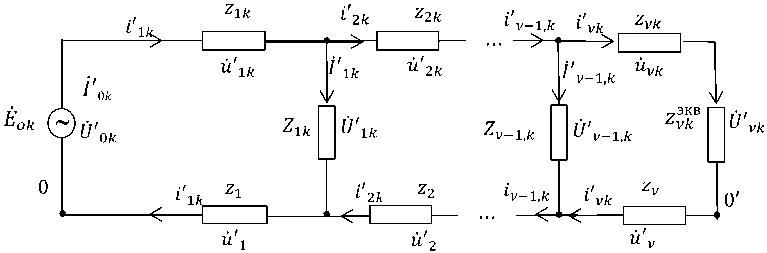
Рис. 3. Схема к -й подсистемы с эквивалентным сопротивлением z ^ _k ^B

Для этих контуров справедливы следующие балансовые соотношения для напряжений:

U _v -l,k = ⁽ z_V k +z_v + z^^B)i_vk,v — 1,n,k — 1,3. (10) По условиям задачи все сопротивления трехфазной сети являются известными величинами, поэтому эквивалентные сопротивления z™ можно вычислить непосредственно по заданной расчетной схеме, показанной на рис. 2. Один из возможных алгоритмов их оценки, имеющий более простую вычислительную схему, изложен в приложении 1.

Отметим, что действующие значения (модулей) токов i'_vk, протекающих в начальных участках фазных проводов, являются известными величинами, так как они измеряются головным трехфазным счетчиком электроэнергии, установленным в трансформаторной подстанции РЭС, и хранятся в базе данных АСКУЭ. При этом модули (действующие значения) u_lk комплексных напряжений u_lk определяются на основе закона Ома: u_lk — I o _kz_lk, где z_lk - модуль сопротивления z_lk (к — 1,3). Для определения остальных межабонентских действующих токов и напряжений сети необходимо найти величины 6_vk, определяемые выражением (9). Для этой цели рассмотрим электрические контуры (v = 2), имеющие координаты (2, к). Для этих контуров соотношения (10) имеют вид (см. рис. 3)

^U lk ^{— (z}2k + ^z2 + ^z2k ⁾ⁱ 2k , ^{k — 1,—} Полученные соотношения с учетом того, что U_lk = Z_lki_lk, запишем в виде

^Zlk ' lk ^{— (z}2k + ^z2 + ^z2k ⁾ⁱ 2k , ^{k — 1} ,3, что эквивалентно следующим соотношениям:

• — Z'^, k — 1,—,                      (11)

• ^l, 2k

где Z'2k - комплексная величина, определяемая по формуле

• ,   _ z₂ k +z₂+z =k

• ^z 2k ^—     ₇      .

^z ik

По условиям задачи сопротивления z_2k, z₂ и Z_lk предварительно определяются и записываются в базу данных АСКУЭ, а также представляются, например, в виде (7). Следовательно, величины Z'_2k можно вычислить и представить в экспоненциальной форме:

Z' 2k — Z' 2k e^iX"^k, k — 13,                   (12)

где Z'_2k, A_2k - модули и аргументы Z'_2k соответственно.

В результате с учетом (5), (6) и (12) соотношения (11) можно записать в следующей экспоненциальной форме:

• ^{5; ik}^ —Z^^lk —13.         (13)

• t^; 2k

Для выполнения соотношений (13) должны соблюдаться равенства модулей и аргументов их левых и правых частей, т. е. должны выполняться следующие условия:

6 2k — ^k, k — 1,3,                        (14)

I lk — Z lk I' lk , k — 1,3.

Таким образом, формулы (14) определяют значения разности фазовых сдвигов 6_2k по исходным данным, полученным с абонентских счетчиков электроэнергии. Здесь следует отметить, что для начальных контуров, имеющих координаты (1, k), можно получить соотношения, аналогичные условиям (14), т. е.

6 lk — « lk -(X lk — Z lk ,k — 13.           (15)

Для этой цели используются балансовые соотношения для напряжений (10) при v — 1. Полученный результат далее будем использовать для идентификации неизмеряемых и неконтролируемых переменных (токов и напряжений) трехфазной сети.

Идентификация действующих токов и напряжений на участках фазных проводов . Для этой цели рассмотрим контуры исходной трехфазной сети, имеющие координаты (2, k). Как видно из рис. 1, межабонентские токи i_2k , протекающие во 2-м участке фазного провода сети, определяются по формулам:

• ⁱ 2k ⁱlk ' lk , ^k     I³-

• Нетрудно показать, что для квадратов модулей ^k этих токов справедливы выражения:

• ^l 2k ^— (i lk ^— ik⁾⁽ⁱlk ^— i^ ^—

• ^{—    (i}lk ^— ik⁾⁽ⁱ*lk ^{— I}*lk^{) —}

——

• ^—    Ik i lk + ' lk ' lk ⁽ⁱlk ^ lk ⁺ i k lk⁾ , ^{k —} 1, ³ , составляющие которых можно определить по формулам:

i , i* , — J²    t , t * — Z²

• ⁱ lkⁱ lk ^{— l}lk , ' lk ' lk ^— ' lk , *                z*

• ⁱ lk^I lk ^{+ I}lkⁱ lk ^—

• —    i_lkI_lk(e ⁷'⁽“ ik ^-s ik ) + e ^-v⁽“ ik ^-8 ik ) ) —

• —    i lk I lk (e^i9ik + e ^{-76 ik} ) — 2Z lk ' lk Cos6 lk , где l_lk,I_lk — действующие значения токов, протекающих через соответствующие сопротивления z_lkuZ_lk. В результате для l 2 _k справедлива следующая формула:

• ^{l 2}k ^{— l2}k ⁺ kk ^— Iklk l^⁸^ + е ^{i6 2k} ] ^—

• —    l l²k + I l²k — 2l lk ' lk cos6 2k , k — 13.

Отсюда с учетом (14) получаем численные значения l 2k :

• ^l2k ^{— l}lk ⁺ ' lk ^{— 2l}lk^Ilk^cos ^- 2k , ^{k —} 1, ^{3 .}

Далее последовательно рассматриваются электрические контуры с координатами (3, k), (4, k), ^, (n —1, k). На основе указанной выше вычислительной процедуры определяем действующие значения токов l_3k, l_4k, _, l_n-l , _k. При этом l_nk — I_nk. Модули соответствующих межабонентских напряжений u:_vk можно определить на основе закона Ома: u_vk — l_vk ^zv _k, где z_vk - модуль сопротивления z_vk (k — 1,3, v — 3, n — 1).

Идентификация действующих токов и напряжений на участках нулевого провода . Рассмотрим исходную структуру трехфазной сети, показанную на рис. 1. Как известно, комплексный ток J_v , протекающий в v -м участке нулевого провода, определяется как сумма [20]:

iv = i vi + i v2 + i v3 .                          (16)

где i_v1, i_v2, i_v3 — межабонентские токи, протекающие через v -й участок фазных проводов. Для первого участка (v = 1) выражение (16) запишется в виде

/1 = 1 11 + 1 12 + I 13 .

Для квадрата модуля J ² комплексного тока j справедливо выражение

J² = ⁽ⁱ11 + I2 ⁺ i 13⁾⁽ i 11 ^{+ i}12 ⁺ йл) * =

= (in + i 12 ⁺ i 13⁾⁽ i *11 ⁺ 1 *12 ^{+ р}13 ) =

= ⁱ11ⁱ 11 ^{+ i}12ⁱ 12 ^{+ i}13ⁱ 13 ^{+ i}11ⁱ 12 ⁺

^{+ i}12ⁱ 13 ^{+ i}13ⁱ 12 ^{+ i}11ⁱ13 ^{+ i}12ⁱ 11 ⁺ Isll , составляющие которого можно определить по следующим формулам:

11 1 11 = ^Z11 , ⁱ12ⁱ 12 = ^Z12 , ⁱ13ⁱ 13 = ^Z13 ,

11 1 12 ^{+ i}12ⁱ 11 =

= Z₁₁Z₁₂(e ^j(“ ii ^-“ i2 ⁾ + _e -7^(an-^a i2 ) ) =

= 2Z 11 Z 12 c ^os(a:11 ^— ct12 ),

11 1 13 ^{+ i}13ⁱ 11 =

= Z₁₁Z₁₃(e ^j(“ ii ^-“ i3 ⁾ + e ^-7(s ii ^-s i³ ) ) =

= ^nZ^costan — <$13), i12i 13 + i13i 12 =

= Z₁₂Z₁₃(e ^j(“ i2 ^-“ i3 ) + _e ^-7(8 i2 ^-“ i3 ) ) =

= 2Z 12 Z 13 c ^os(< $ 12 ^— C? 13 ).

С учетом полученных выражений квадрат модуля тока J 1 определяется по формуле

/1 = ^Z11 ^{+ Z}12 ^{+ Z}13 ⁺ 2 ^Z11^Z12^C0S U 1 ⁺

+2ZnZ 13 COS^ 2 + 2Z 12 Z 13 COSU 3 .

где для разностей фазовых сдвигов введены следующие обозначения:

^ 1 = « 11 ^— « 12 , ^ 2 = « 11 ^— « 13 ,

U 3 = « 12 ^— « 13 -                            ⁽¹⁷⁾

Отметим, что на основе рассмотрения новых подсистем (см. рис. 2), полученных путем декомпозиции исходной структуры трехфазной сети, можно найти численные значения ^ъ ^2, ^3 указанных выше разностей ^ъ ^2 и ^3, т. е.

Л 1 = Л 1 , ^ 2 =^ 2 , ^ 3 =^ 3 .                 (18)

Доказательство этого факта приведено в приложении 2.

В результате искомое действующее значение тока J₁, протекающего в первом участке (v = 1) нулевого провода, определяется следующим выражением:

/1 = (Z^ + Z^ ^{+ Z}13 ⁺ 2Z 11 Z 12 c ^0S ^ 1 ⁺

+2Z 12 < 13 COS^ 2 + 2W 13 COSU 3 ) ³ .

Далее на основе изложенного выше алгоритма можно вычислить действующие значения токов /₂, /₃, ..., /„. Модули соответствующих межабонентских комплексных напряжений u_v определяются на основе закона Ома: u_v = J_vz_v, где z_v - модуль сопротивления z_v (v = 1,n).

Приложение 1 . Для определения эквивалентных сопротивлений запишем выражения для комплексных мощностей P_k, потребляемых к -й фазой трехфазной сети (см. рис. 1):

^Pok = ^Pok ^{+ jQ}ok , ^k = 1,3,               (П. 1)

где Р_ок , Q_ok - активные и реактивные мощности соответственно, численные значения которых можно вычислить по исходным данным задачи по формулам:

Р ок = l ok U ok cos Ф ок , Q ok = l ok U ok sin Ф ок .

С другой стороны, выражения для этих мощностей можно записать в виде следующей суммы:

P ok = P 1k + P lk + P1fc, ^p = 1,3, где

P , — ₇ , /² p^o — 7 /² p^ _ экввгг.

^P1k = ^z1k^Z1k , ^P1k = ^z1^Z1k , ^P1k = ^z1k ^Z1k^.

Таким образом, имеем

P ok = ^(z1k + 2 1 )1^ + z ^эk^в Z ¹k .            (П. 2)

Приравнивая правые части выражений (П. 1) и (П. 2), получаем

P ok +jQ ok = ⁽ 2 1k + z^ k + z1™l¹ k ,k = 13. Отсюда находим z^™:

экв _ Pk +jQ k^-(zik + ^zL >l ik     _ 1"^3

^z1k               ,2            , ^    1,3.

^£ ik

Далее для определения z^™ используются следующие выражения, определяющие балансовые соотношения для комплексных мощностей относительно контуров, имеющих координаты (2, к):

^Pok = ^P1k ^{+ P}1k ^{+ Р} 1k ^{+ P}2k ⁺

+P 2^ok + P 2k ,k = 1,3,                    (П. 3)

где составляющие суммы определяются по формулам:

^P1k = ^z1k^Zlk , ^Plk = ^z1^Zlk , ^P ' 1k = ^ 1k⁷lk ,

^{2 o} /² p^     экввгг.

^P2k = ^z2k^Z2k , ^P2k = ^z2^Z2k , ^P2k = ^z2k ^Z2k , а мощность P_ok задается формулой (П. 1).

Таким образом, соотношение (П. 3) можно записать в виде

^Pok ^{+ jQ}ok = ^(z1k ^{+ z}1^)Zlk ^{+ (z}2k ^{+ z}2^)Z2k ⁺

4-7.1 ² 4- 7³™]²

^+z1k ' 1k ^{+ z}2k ^Z2k .

Отсюда определяем экв _ pok+jQok-(zik+zi)iik-(z2k+z2)*2k-zikL2k z2k =                       >2                        .

^£ 2k

Аналогичным образом можно найти и другие эквивалентные сопротивления z Vk^B , определяемые выражениями:

z Vk^B = ^, v = 3,n- 1, к = 13.

Приложение 2. Рассмотрим исходную схему трехфазной сети (см. рис. 1) и контуры, имеющие координаты (1,к). Для этих контуров балансовые соотношения для напряжений имеют вид йок = й1к + й1 + й1к,к = 13,         (П. 4)

которые представим в виде

й1 = й0к-й1к-й1к,к = т,з.

Правые части последних соотношений запишем через соответствующие токи и сопротивления: экв

« 1 = l lk^zOk    7 1к ^ 1к l 1k^z1k =

= 1 1к № - 2 1к ) - 1 1к 2 1к , к = 1,3,     (П. 5)

где zO™ - эквивалентное сопротивление к -й фазы, определяемое по формуле

-экв _ fofc , _ zOk = , , к = 1,3,

‘ifc где Рок - комплексная мощность, потребляемая к-й фазой трехфазной сети, определяемая по формуле (П. 1). С учетом (1) и (3) соотношения (П. 5) имеют вид

« 1 = Z 1k e ⁷'(^ ^{fc +a lk} )^(zOk^{в - z}1k^{) -}

-ккЕ^1^"^, к = U.

С учетом (15) получаем

U1 = кке7^®1^3™ - Z1k) -

-Л../.^^^"^^^^ = 13, что эквивалентно следующим соотношениям:

й1 = [Z1k(zэkв - z^^k - / , / , е'■■ + ■ |е' -, к = 1,3.                                    (П. 6)

Введем обозначения

Е1к = [Z1k(zOkв - Z1k) - 11к21кв^^Гк,

к = й.

Отметим, что значения Е_1к можно вычислить и представить в экспоненциальной форме

Е1к = Е^е7^, к = 13,              (П. 7)

где Е_1к , ^_1к - модуль и аргумент комплексной величины Е_1к соответственно, которые являются известными величинами.

В результате соотношения (П. 6) с учетом (П. 7) имеют вид

й1 = Е1ке=^1ке^$1к, к = 13.             (П. 8)

Теперь соотношения (П. 8) запишем для каждой фазы (к = 1,3):

й₁ = Е₁₁е ⁷^ ¹¹ е ⁷'^{й 11} ,

й1 = Е12е)^12е)Й12,

й1 = Е13е)^12е)а12.

Путем деления соответствующих левых и правых частей первого уравнения на соответствующие части второго и третьего уравнений, а также второго уравнения на третье получаем следующие равенства:

р11еК^11-512)еК“11-“12)

К"2= 1

Р 11 _е 7⁽?11-?1з) _е 7⁽“11~“1з)

ЁГз= 1

Г(^12^;1з)рУ(а12-а1з) ‘ 12е^

F13= которые эквивалентны соотношениям:

Е₁₁е ^;'⁽“ 11 ^-“ 12 ⁾ = Е₁₂е ⁷'⁽^ 12 ^-^ 11 ) ,

Е₁₁е ^7(йи-^гг 1з ⁾ = Е₁₃е ⁷⁽^ 1³ -^ 11 ) ,            (П. 9)

Е₁₂е ⁷⁽“ 12 ^-“ 1^{з )} = Е₁₃е ⁷⁽^ 1^{3 -}^ 12 ) .

Для выполнения системы соотношений (П. 9) должны соблюдаться равенства модулей и аргументов их левых и правых частей, т. е., в частности, должны выполняться следующие условия:

£^ 11 ^- «и = f 12 ^- f 11 ,

<$ 11 - « 1з = f 13 - fn,                  (П. 10)

« 12 ^- « 13 = ^f13 ^{- f}12 .

С учетом обозначений (17) получаем, что численные значения разностей ^1, ^2, ^3 фазовых сдвигов определяются по формулам:

U 1 = ^f12 ^{- f}11 , U 2 = ^f13 ^{- f}11 , U 3 = ^f13 ^{- f}12 , где величины f₁₁, f₁₂ и f₁₃ являются известными, что подтверждает справедливость соотношений (18).

Выводы

Предложен новый метод идентификации не-измеряемых параметров (токов и напряжений), определяющих электрические состояния межабонентских участков трехфазной распределительной сети, функционирующей в условиях несимметрии токов и напряжений. Считается, что трехфазная сеть относится к классу линейных систем, что дало возможность ее исследовать как систему, состоящую из трех условно автономных подсистем. В качестве последних рассматриваются ее электрические фазы, на входы которых поступают воздействия в виде отдельных ЭДС, формируемых источником питания сети. Отличительная особенность предложенного метода состоит в том, что реализация процедуры идентификации осуществляется непосредственно по исходным данным АСКУЭ, полученным с абонентских счетчиков электроэнергии по каналам связи. При этом не требуется построение математической модели трехфазной сети, основанной на представлении токов и напряжений в комплексной форме, что упрощает вычислительную схему метода. Полученные результаты ориентированы для создания специального программного обеспечения подсистемы идентификации и оперативного мониторинга потерь электроэнергии в распределительной сети в составе АСКУЭ.