К проблеме локализации утечек тока в распределительной сети по данным АСКУЭ

Как известно [1, 2], к числу важнейших показателей качества и эффективности работы распределительной электрической сети (РЭС) относятся потери электроэнергии в ней, состоящие в основном из технических и коммерческих потерь. В целях экономии энергоресурсов при эксплуатации РЭС необходимо разрабатывать и принимать практические меры, направленные на минимизацию этих потерь. В частности, для снижения технических потерь электроэнергии к настоящему времени предложен ряд способов и средств [3–6]. В то же время практически отсутствуют методы и средства для снижения коммерческих потерь электроэнергии, к которым относятся утечки токов, вызванные в частности несанкционированным отбором электроэнергии. Анализ показывает, что наиболее эффективный путь значительного снижения потерь электроэнергии состоит в разработке и внедрении дополнительных подсистем в составе существующих АСКУЭ [7], ориентированных на выполнение таких важных функций, как оптимизация режимов работы РЭС [8–10], а также идентификация и локализация мест несанкционированного отбора электроэнергии в сети [11, 12]. Непосредственное применение известных математических моделей [13–15] и методов [16–19] для этих целей представляет определенные трудности, так как при этом необходимо учитывать ряд факторов, таких как несимметрия токов и напряжений в сети [20, 21], случайный характер утечек тока, а также необходимость решения соответствующих функциональных задач в режиме реального времени [7]. В [12, 22] предложены подходы к идентификации и локализации мест утечек тока, включая несанкционированные отборы электроэнергии, в распределительной сети напряжением 0,4 кВ на основе комплексного представления ее переменных (токов, напряжений). Данная работа посвящена вопросам развития этих подходов. При этом задача идентификации решается без предварительного построения модели трехфазной сети в комплексной форме [23], что значительно упрощает вычислительную процедуру локализации координаты несанкционированного потребителя электроэнергии в сети.

Постановка задачи

Рассматривается четырехпроводная трехфазная сеть с напряжением 0,4 кВ, расчетная схема которой показана на рис. 1. Здесь k,v - индексные переменные, обозна ча ющие соответственно номера фаз А, В, С (k = 1,3) и электрических контуров сети (v = 1,n); 7_vk, U_vk - синусоидальные мгновенные ток и напряжение на соответствующем электроприемнике (нагрузке) с координатой ( v , k); i_vk, z_vk - мгновенный ток и сопротивление v -го межабонентского участка (МАУ) k-й фазы; й у _к, &_v — напряжения соответственно на v -м МАУ k-й фазы и нейтрального провода; J_v,z_v - мгновенный ток и сопротивление ν -го участка нейтрального провода; U_k , I_k = i_lk - мгновенные синусоидальные напряжения и токи соответственно на входах соответствующих фаз.

Далее предполагается, что выполняются следующие условия.

• 1.    Распределительная сеть относится к классу линейных систем и функционирует в несиметрич-ном режиме.

  

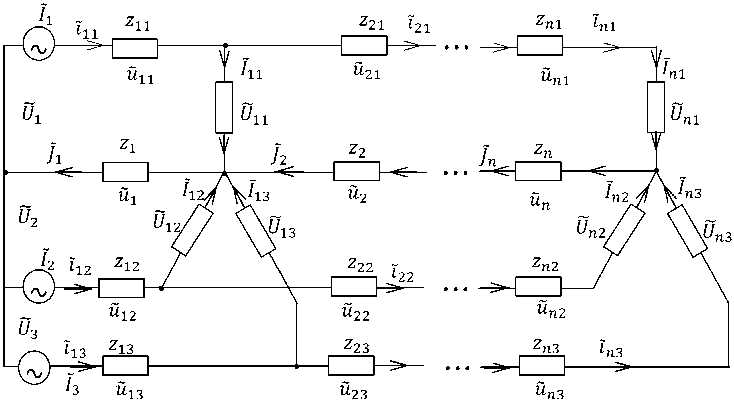
  Рис. 1. Расчетная схема трехфазной сети

  
  

• 2.    Линейные и нейтральный провода сети имеют разные сечения.

• 3.    Ток утечки отводится через нейтральный провод сети.

• 4.    База данных АСКУЭ содержит текущие значения сопротивлений z_vk и z_v межабонентских участков (МАУ), представленных в комплексной форме [16, 23].

• 5.    Периодически в дискретные моменты времени t Е [t ^ , t ^ ₊₁] подсистема сбора данных АСКУЭ осуществляет опрос абонентских счетчиков электроэнергии с шагом дискретизации At ^ = t ^ ₊₁ — t ^ , где f = 1,2, ... . На основе измерительной информации в автоматизированной системе формируются исходные данные задачи подмножества I_t, U_t и ф_t , состоящие из действующих токов I_vk и напряжений U_vk на соответствующих нагрузках и сдвигов фаз ф ^ _к между ними:

^It = ^{Ivk ) nx3 ,

U t = {U_V k ) nx3 ,                               (1)

Ф t ^{ Ф ^к } пх3 ^.

Задача состоит в идентификации и локализации мест утечек тока в распределительной сети.

Метод решения задачи

Решение сформулированной задачи состоит из следующих основных этапов:

• 1)    идентификация наличия в сети утечек тока;

• 2)    оценка параметров тока утечки;

• 3)    формирование критерия локализации координаты несанкционированного потребителя;

• 4)    локализация координаты несанкционированного потребителя.

Идентификация наличия в сети утечек тока. В каждый момент времени t Е [t ^ , t ^ ₊₁] суммарные токи на входах фаз I_k(t) (к = 1,3) , потребляемые абонентами сети в соответствующих фазах, определяются выражениями:

№ = 2"=1Ы0, к = 1Д

Распределительная сеть характеризуется следующими состояниями [12]:

• 1)    нормальное (желаемое) состояние S⁰;

• 2)    возмущенное состояние S ’ .

• В нормальном состоянии (S⁰) в РЭС отсутствует утечка тока и для всех t Е [t ^ , t ^ ₊₁] выполняются следующие соотношения:

IWO- I k (t)l max , к=ТЗ,        (2)

где I_ok(t) - действующий ток на входе к -го линейного (фазного) провода, измеряемый счетчиком электроэнергии (Сч) на выходе источника питания - трансформаторной подстанции (ТП); AI_max -максимально допустимая погрешность измерения токов.

В случае, когда хотя бы одно из условий (2) не выполняется сеть переходит в возмущенное состояние S ’ , что обуславливается наличием в ней утечек тока.

Анализ показывает, что использование условий (2) для выявления факта утечек тока в сети представляет определенные сложности, что связано с необходимостью предварительного определения неизвестных фазовых сдвигов абонентских синусоидальных токов 7vk(t), которые в установившемся режиме определяются выражениями [16]:

7 vk (t) = I ^k ^axsin(^t + a vk ), v = Т"п, к = 13, где I_v^m_k^ax, <^_vk — амплитуда и фаза синусоидального тока соответственно, определяемые формулами:

Ivk     V2Ivk, ^vk   ^vk + ^vk, avk — приращение фазового сдвига относительно базового значения ^k, которое определяется фор-2(k-1)^ мулой ^vk =  3 .

В целях упрощения решения сформулированной выше задачи предварительно выполним декомпозицию структуры исходной трехфазной сети (см. рис. 1), предполагая, что она относится к классу линейных систем. С учетом свойства линейности ее можно расчленить на три электриче-

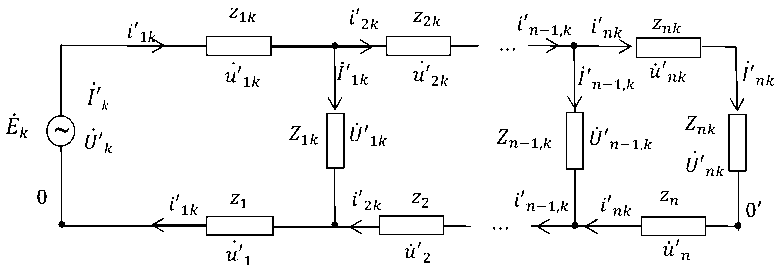
Рис. 2. Структура k -й подсистемы распределительной сети

ские цепи (подсистемы), каждая из которых представляет собой соответствующую фазу сети при отключенном состоянии двух других фаз (рис. 2).

Эти подсистемы можно рассматривать как условно независимые (автономные) структуры, на входах которых действуют ЭДС Ё₁ , Ё₂ и Ё₃ , формируемые источником питания (ТП) сети. При этом комплексные токи / '_vk и напряжения U'_vk на нагрузках, а также межабонентские токи i'_vk и напряжения И '_vk , И '_v новых подсистем отличаются от прежних их значений (см. рис. 1). В частности, комплексные токи I '_vk , i¹_vk и напряжения U¹_vk можно представить следующими выражениями:

I vk = I'vk^^^ ^ ,

U'vk = U'vk^ ,

i'vk = I'vkej^k, v = 1333, к = 133.

где I 'vk , U' vk , ^; 'vk , “ vk , V vk , Ik — модули и аргументы соответствующих комплексных переменных, которые являются неизвестными величинами.

В отличие от токов и напряжений при такой декомпозиции значения комплексных сопротивлений (Z_vk , z_vk , z_k ) исходной трехфазной сети сохраняются, т. е. не изменяются. В частности, сопротивления нагрузок Z_vk можно представить в виде —       * _                ------- _       ------

Z vk = Z vk 6^{m k} , v = 1,n, к = 1,3,         (3)

где Z_vk , ф_vk - модули и аргументы соответствующих комплексных сопротивлений Z_vk соответственно, определяемые по исходным данным задачи:

Z vk = ~. V vk = arccos c_V k , c_vk = cos^ vk .

^ vk

Теперь на основе указанной выше декомпозиции для выявления факта утечек тока в сети представляется возможным вместо условий (2) использовать другие соотношения, определяемые только известными сопротивлениями элементов трехфазной сети и отдельных ее цепей. Для этой цели рассмотрим эквивалентные сопротивления упрощенных цепей (фаз) z k и z_k, вычисленных соответственно для нормального 5 ° и возмущенного 5’ состояний сети. При этом оценки сопротивлений z_k можно вычислить по данным головного трехфазного счетчика электроэнергии, установленного в ТП:

z_к = ^еМ = £e^' k , к = 13,        (4)

!ok где I°k, U°k, фк - действующие значения напряжения U°k и тока I°k на входе к-й фазы и соответствующие коэффициенты мощности; zk — модуль комплексного сопротивления zk.

Для вычисления эквивалентных сопротивлений zk можно использовать известный способ их определения для последовательно-параллельного соединения электрических цепей [16] и представить их в виде z° = z°ke^k, к = 13, (5) где zk, Фk — модуль и аргумент комплексной величины zk соответственно. При этом используются комплексные сопротивления нагрузок сети, представленные в виде (3).

Теперь для того, чтобы определить факт наличия утечки тока в k -й фазе сети в данном интервале наблюдения [t ^ , t ^ ₊₁], вместо соотношений (2) на основе выражений (4) и (5) имеется возможность использования следующих условий:

|z ° —z k |max, к = 1Д (6) где ^z_max - малое положительное число, определяющее максимально допустимое значение разностей (z k — z'k ).

Очевидно, что при выполнении условий (6) в k -й фазе сети отсутствует утечка тока, а при их невыполнении – она присутствует.

Оценка параметров тока утечки . Для этой цели вначале осуществляется декомпозиция исходной структуры трехфазной сети, в результате которой формируются три подсистемы, которые показаны на рис. 2. По условиям задачи сопротивления нагрузок Z_vk и межабонентских участков z_vk , z_v являются известными величинами.

Предположим, что утечка тока происходит в ^ -й фазе сети. Тогда комплексная мощность Р_м, отдаваемая µ -й фазе, в возмущенном состоянии сети 5 ’ определяется выражением

Р д = (I m )²z'„ , _ (7) где I ° _д - действующее значение тока Г_д на входе µ -й фазы, измеряемое головным трехфазным счетчиком электроэнергии; z^^ - эквивалентное сопротивление µ -й фазы, которое определяется по формуле (2). В невозмущенном состоянии

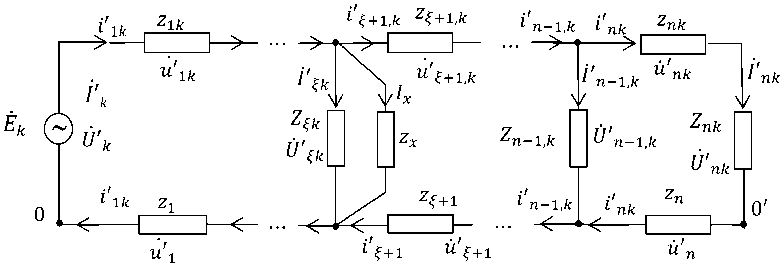
Рис. 3. Схема подключения сопротивления z _x

рассматриваемая мощность определяется выра- жением

Р Ц = СЮ)²^? ,                      _      (8)

где 1 0 , z O - действующее значение тока Т О на входе µ -й фазы и эквивалентное сопротивление. Величина z O определяется выражением (3). Для оценки тока Г О рассмотрим функциональную зависимость между выходом источника питания (ТП) и входными переменными µ -й фазы:

Е о = U 0 + l £ z,                           (9)

где Ео, z - действующее значение э.д.с. источника и его внутреннее сопротивление соответственно; иО — действующее значение напряжения на входе невозмущенной µ-й фазы. С учетом того, что UОО = 100^0, соотношение (9) запишется в виде

^Ео = ( ^Z0 ^{+ z)1}0 .

Отсюда получаем оценку величины Г О : о=^ ¹⁰ z^z*

С учетом выражения (10) формула (8) для плексной мощности рО принимает вид рО _ ^И р (^*

ком-

Очевидно, что мощность ^Р0, потребляемая несанкционированным потребителем, определяется разностью др = р' - рО

О О О , которая с учетом (7) и (11) имеет вид

/ХР = ‘Г ²z' —!И_

^^r O    ⁽¹ О ) ^Z O (z^y'                   ^{( )}

С другой стороны, для ДР0О справедлива формула

^Р о = !^лх ,                            (13)

где 1_Х , z_лХ - действующее значение тока утечки и комплексное сопротивление межабонентского участка рассматриваемой фазы от источника до места подключения НОЭ соответственно, определяемые следующими выражениями:

1_х = 1' о - 1 0 ,                                  (14)

^Zл x ^Zл ^{+ z}x ,                                ⁽¹⁵⁾

zx - комплексное сопротивление нагрузки несанкционированного потребителя. При этом величина тока 1Х является известной величиной. Теперь, приравнивая правые части соотношений (12) и (13), получаем равенство а’ )2z' _        = /2z

⁽¹О ) ^ZO (z ° _+z) 2 ^1xZ”^x "

Отсюда с учетом (14) получаем формулу для оп- ределения сопротивления несанкционированного потребителя zx :

z_x =

^(Ip?)^2z ^ ^Ix^z л        EpZp.

----- ----—-----.

l £          I x (^z^^+z)²

Л            Л pv

Таким образом, найдены параметры несанкциони- рованного потребителя, которые определяются формулами (14) и (16).

Критерий локализации координаты несанкционированного потребителя. Для этой цели со- противление неизвестной нагрузки zx подключаем параллельно к некоторой другой произвольной нагрузке. Например, к нагрузке, имеющей координату (f, р), что показано на рис. 3. При этом сопро тивление zл по условиям задачи является известной величиной, а zx определяется формулой (16).

Далее вычисляем эквивалентное сопротивление Z₀ рассматриваемой фазы, которое является функцией от сопротивления z_x и номера f пока неизвестного контура, к которому подключен несанкционированный потребитель, т. е. Z₀=Z₀(f, z _x ). Введем следующую функцию:

^Eo^(f , ^zx^ = ^^^zol ^{— Z}o^(f , ^Zx )\, ⁽¹⁷⁾ где z₀ - известное эквивалентное сопротивление, которое вычисляется по формуле (2) и характеризует возмущенное состояние сети S ’.

Анализ показывает, что нулевое (или близкое к нулю) значение функции F₀(f,z_x") достигается при значении f = f * , которое определяет координату несанкционированного потребителя ( f * ,p ). Таким образом, F₀(f,z_x) по существу является критериальной функцией для отыскания искомой координаты.

Локализация координаты несанкционированного потребителя. Для этой цели сопротивление zx подключаем параллельно к другой нагрузке, например, с координатой (р, f + 1) и находим величину соответствующего сопротивления Z0(f,zx) и значение функции F0(f + 1,zx). Продолжая этот процесс, решаем следующую экстремальную задачу:

min^№z_x) = F(r,z_x), (18) где £ - дискретное множество, состоящее из натуральных чисел v = 1,2, ...,п, определяющих номера контуров рассматриваемой фазы (к = ^); f * - номер контура, определяющий минимальное значение функции F(f * ,z_x). При этом целое число f * , найденное в результате решения экстремальной задачи (18), определяет координату (f * ,^) несанкционированного потребителя, подключенного к µ -й фазе трехфазной сети. Полученные результаты позволяют сформулировать следующий алгоритм локализации координаты несанкционированного потребителя:

• 1)    опрос счетчиков электроэнергии, запись в базу данных АСКУЭ исходных данных, представленных в виде (1);

• 2)    определение фазы, к которой подключен несанкционированный потребитель (к = ^);

• 3)    вычисление эквивалентных сопротивлений z ^ и z ^ фаз, которые определяются для возмущенного 5' и невозмущенного 5 ° состояний сети, и представление их в виде (4) и (5);

• 4)    оценка комплексных мощностей фаз Р ^ и Р ° которые определяются для возмущенного 5' и невозмущенного 5 ° состояний сети, по формулам (7) и (8);

• 5)    определение потери мощности Др^, вызванные из-за подключения к сети НОЭ, оценка которых вычисляется по формуле (12);

• 6)    оценка сопротивления нагрузки z_x несанкционированного потребителя по формуле (16);

• 7)    формирование критериальных функций Fz(f,z_x), определяемых выражением (16);

• 8)    определение координаты (f * ,^) несанкционированного потребителя на основе решения экстремальной задачи (17).

Выводы

Предложен новый метод идентификации и локализации координаты несанкционированного отбора электроэнергии в несимметричных распределительных сетях напряжением 0,4 кВ. Идея идентификации основана на декомпозиции исходной трехфазной сети на более простые, относительно автономные структурные составляющие (подсистемы), каждая из которых представляет собой соответствующую фазу сети при отключенном состоянии двух других фаз. Найдены условия, при выполнении которых идентифицируется факт наличия несанкционированного отбора электроэнергии в сети. Предложен конструктивный критерий, определяющий математические условия, при выполнении которых обеспечивается локализация координаты утечек тока в сети. Формирование указанного критерия осуществляется на основе оценки неизвестного сопротивления нагрузки несанкционированного потребителя. При этом отпадает необходимость предварительного построения математической модели трехфазной распределительной сети, что значительно упрощает вычислительную процедуру метода. Полученные результаты можно использовать для создания алгоритмического и специального программного обеспечения подсистемы идентификации и мониторинга потерь электроэнергии в трехфазной распределительной сети в составе АСКУЭ.