К проблеме моделирования несимметричных распределительных электрических сетей в составе АСКУЭ

Распределительные электрические сети напряжением 0,4 кВ являются конечными звеньями отпуска электроэнергии потребителям как товарной продукции. Как известно, повышение качества и эффективности функционирования РЭС во многом достигается на основе внедрения современных технологий, таких как автоматизированные системы контроля и учета электроэнергии (АСКУЭ) [1]. Основными структурными и функциональными элементами этих систем являются концентраторы данных (КД), комплекс счетчиков электроэнергии (Сч), установленных у абонентов сети. Для обмена технологической и служебной информацией между подсистемами АСКУЭ в составе КД и Сч имеются телекоммуникационные модули (ТКМ), построенные с использованием современных технологий передачи данных (GSM, Zigbee, PLC и др.). Основные функции КД: оперативный сбор данных с группы счетчиков электроэнергии (Сч); хранение полученных данных; цифровая обработка информации по решению соответствующих функциональных задач; обмен информацией с верхним уровнем управления. Необходимо отметить, что в настоящее время в рамках АСКУЭ, в основном, решаются задачи коммерческого учета электроэнергии. В то же время в целях повышения эффективности автоматизированных систем наиболее актуальной является включение в ее состав таких важных функциональных задач, как оперативный мониторинг [2], диагностика состояний [3–5] и оптимизация режимов работы РЭС [6–9]. Основу решения указанных задач составляют математические модели и методы, позволяющие в режиме реального времени идентифицировать неизмеряе-мые и неконтролируемые переменные (токи, напряжения) трехфазной сети, что дает возможность определить такие ее показатели качества как фактические потери электроэнергии, а также оценить реальные значения параметров (сопротивлений) магистральной линии с использованием измерительных данных. Применение известных моделей и методов [10–12], в частности, метода симметричных составляющих [13, 14], для этой цели представляет определенные трудности, к числу которых можно отнести следующие факторы:

• •    несимметрия токов и напряжений в трехфазной сети;

• •    неопределенность текущих (реальных) значений сопротивлений межабонентских участков

магистральной линии (МЛ), которые изменяются случайным образом в зависимости от внешних условий (температуры, влажности);

• •    счетчиками электроэнергии (Сч) измеряются лишь действующие значения токов и напряжений на нагрузках потребителей электроэнергии, что не позволяет для математического описания процессов в РЭС непосредственно использовать известные физические законы.

Указанные факторы сдерживают построение достаточно эффективных моделей, описывающих физические процессы в РЭС, что не позволяет в полной мере решать задачи моделирования и мониторинга состояний распределительных сетей. В работе предлагается методология построения модели несимметричной трехфазной сети и идентификации недоступных для измерения ее электрических переменных в режиме реального времени. Полученные результаты ориентированы для применения в составе АСКУЭ в целях оперативного мониторинга электрического состояния РЭС и оценки потерь электроэнергии в сети.

Постановка задачи

Рассматривается трехфазная РЭС с напряжением 0,4 кВ, расчетная схема которой показана на рис. 1.

Предполагается, что сеть функционирует в несимметричном режиме. Для удобства на рис. 1 фазы А, В, С пронумерованы соответственно через индексную переменную к (к = 1,3). Остальные обозначения имеют следующий смысл: ЕА,ЕВ,ЕС -мгновенные фазные ЭДС; Zvk - обозначение v-й нагрузки (электроприемника) (v = 1,п), подключенной к фазе с номером к; Ivk, Uvk - мгновенные ток и напряжение на нагрузке Zvk; ivk,zvk - мгновенный ток и сопротивление v-го межабонентского участка (МАУ) к-й фазы; uvk, uv - мгновенные напряжения соответственно на v-м МАУ к-й фазы и нейтрального провода; Jv, zv - мгновенный ток и сопротивление v-го участка нейтрального провода; Uok, 4k = Iok - мгновенные напряжения и токи соответственно на входах соответствующих фаз.

Далее предполагается, что выполняются следующие условия:

• 1)    РЭС функционирует в штатном (нормальном) режиме;

• 2)    фазные и нейтральные провода сети имеют одинаковые сечения, т. е. сопротивления z_vk = z_v (к = 1,3, v = 1,п), которые являются априори неизвестными;

• 3)    в системе используются технические средства для подавления высших гармонических составляющих токов и напряжений в сети;

• 4)    со счетчиков электроэнергии (C4_vk) в концентратор (КД) по каналам связи в дискретные моменты времени t Е [t ^ , t ^ ₊₁] с шагом дискретизации At ^ = t ^ ₊₁ — t ^ (f = 1,2, ...) поступают следующие данные:

• •    действующие значения токов I_vk и напряжений U_vk на нагрузках Z_vk ;

• •    коэффициенты мощности cosф_vk , определяемые фазовыми сдвигами ф_vk между соответствующими напряжениями U_vk и токами I_vk .

Как известно [13], мгновенные синусоидальные токи I_vk(t) и напряжения U_vk(t) на нагрузках Z_vk с периодом Т определяются следующими соотношениями:

^I vk ^(t) = ^I- S^ax siⁿ⁽w^t + a_V k ), ⁽¹⁾

UVk(t) = U™kaxsin(^t + ^k), v = 1,п, к = 1,3, (2) где lVkax, UVkax,«vk, ^vk, to - амплитуды, фазы и круговая частота соответственно токов и напряжений (lVkax = V2Ivk, UVkax = ^2Uvk,to = 2пТ-1).

Выражениям (1) и (2) эквивалентны их представления в комплексной форме [13]:

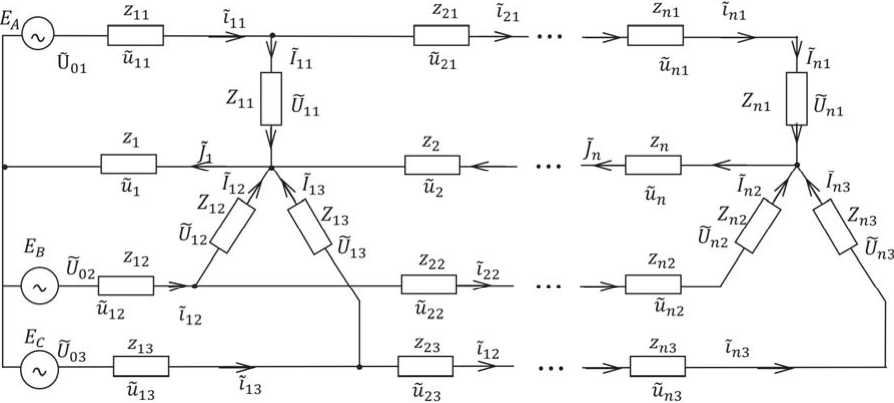
Рис. 1. Расчетная схема трехфазной РЭС

• ^ = 1^1^ = ^“^ ,         (3)

Uvk = U^k + jUk = lUe^k, v = 1,n, к = 1,3,                           (4)

где символы в и м обозначают вещественные и мнимые части соответствующих комплексных переменных; j = V—1 — мнимое число.

Введем следующую систему комплексных векторов:

^Ik   Uok^ik ’ "■’ ⁱnk^] ,

^к     t^lk, ^2k’ •“ , ^n-i,k], йк = [ uOk,u1k.....U„k],

U k = [ u. ik ,u. 2k ,-,u. n-ik A,                   (⁵)

U = [ ti i ,U 2,...,u _u -i ],

J = [ J1.J2 Jn-i], k = 1,3.

Полное текущее состояние рассматриваемой распределительной сети в произвольный момент времени t определяется указанными векторами, которые будем обозначать жирными буквами. Их компоненты далее именуются переменными состояния сети.

Теперь предположим, что в момент времени t Е [t_i,t₂] путем опроса счетчиков электроэнергии (C4_vk) в базу данных концентратора (КД) поступили данные измерений, т. е. модули компонентов векторов I k , U k и соответствующие коэффициенты мощности cosф_vk (v = 1,п, к = 1,3). Задача заключается в том, чтобы на основе этих данных построить модель рассматриваемой трехфазной сети и идентифицировать неизмеряемые и неконтролируемые переменные ее состояния, т. е. оценить компоненты векторов i k , J, U k и и .

Технология решения задачи

Необходимо отметить, что измерительные данные, полученные со счетчиков электроэнергии недостаточны для решения сформулированной задачи. В целях ее решения необходимо найти такой способ, который позволил бы имеющиеся исходные данные преобразовать в комплексные токи и напряжения на нагрузках Zvk, описанные в (3) и (4). Это дает возможность корректно использовать законы Кирхгофа для определения искомых переменных состояния сети. Основная идея при этом состоит в следующем. Вначале на основе информации о коэффициентах мощности (cosфvk) определяются фазовые сдвиги avk и ^vk токов ivk и напряжений Uvk соответственно. Далее эти данные используются для нахождения вещественных и мнимых частей комплексных переменных Ivk и Uvk, характеризующих состояния нагрузок Zvk трехфазной сети. Для выполнения указанных вычислительных операций предлагается использовать специальный преобразователь - вычислительный (программный) модуль в составе концентратора (КД), названный идентификатором динамики нагрузки (ИДН), который предназначен для восстановления установившихся процессов в электроприемнике. Схема преобразования данных с применением такого идентификатора показана на рис. 2.

Далее выходные переменные ИДН используются для оценки искомых переменных состояния трехфазной сети. В результате решение рассматриваемой задачи включает следующие основные этапы:

• 1.    Сбор измерительных данных со счетчиков электроэнергии (C4_vk) и их запись в базу данных концентратора (КД) .

• 2.    Синтез идентификатора динамики нагрузки (ИДН).

• 3.    Оценка токов и напряжений, определяющих состояния межабонентских участков МЛ трехфазной сети.

Синтез идентификатора динамики нагрузки

По условиям задачи счетчиками электроэнергии (C4_vk), установленными у абонентов сети, измеряются лишь действующие значения токов i_vk и напряжений U_vk , а их фазовые сдвиги a_vk иф_vk яв-ляются неизвестными величинами. Как известно, последние для несимметричной трехфазной сети определяются следующими выражениями [13]:

« vi = « vi ,

« v2 = « v2 - 2п/3,

« vs = « vs — 4^ ^/ 3,

^_v i = ^w                          (6)

^ V2 = ^ v2 — 2п ^/ 3,

^vs = $v3 — W, где ^vk Фvk + «vk, k   1,3, v 1, П.

Поставим задачу нахождения неизвестных величин a_vk и ^_vk , входящих в выражения (6). Введем следующие новые комплексные переменные:

ivk =^, Vvk=^, v = Vix, к= 13, ‘vk          uvk где iv,k, uv,k - заданные константы, определяющие

Нагрузка Zvk	ivk№t	Счетчик электроэнергии Счук		Идентификатор динамики нагрузки (ИДН)	*vk
			Uvk
	UvkWt
					Uvk
			COS

Рис. 2. Схема преобразования данных с использованием ИДН некоторые базовые (номинальные) значения действующих токов и напряжений. При этом их значения должны удовлетворять следующим условиям:

UVk = ZvkIVk, v _ Т.п, к _ 1,3, где zVk = UVk/IVk.

Тогда выражения для относительных комплексных переменных имеют вид lvk = lVk +Л"к = W^,

V vk = V vk +jv %k = V vke* ^k,v = Т"й,к = 1,3,

СА _ ABsin^_vi _ ABsin(y_vi — g_vi) _ sin^_vi         sin^_vi

_ ABsin(^_vi+p_vi)

sin^_vi      .

Для определения отрезка ОС рассмотрим треугольник ОСЕ. Как видно из рис. 3 СЕ _ l V _l = l_vlsina_vl. Тогда отрезок ОС можно вычислить по формуле

ОС =

CF sin^ _v i

l vi sin(^ _v i —^ _v i ) sin^ _v i     ^.

В результате соотношение (10) с учетом (11) и (12) имеет вид

где их модули:

I_yk          U^k lvk ?* , Vvk     у* .

Вначале рассмотрим задачу определения фазовых сдвигов ^_vl = ^_vl мгновенных напряжений U_vl на нагрузках Z_vl, подключенных к фазе А (к = 1). Геометрическое представление комплексных переменных l_vl и V_vl показано на рис. 3, где АО = V vl , ВО = l vl .

Из рис. 3 видно, что отрезок АВ и угол p_vl можно вычислить, используя теорему косинусов [15]:

АВ = V^Vl + lVl — 2VviIviCOSVvi,(8)

Vvi +AB2—l$1\ p = arccos I —— ), pvl                2vvlAB а для соответствующих углов справедливы формулы:

Y vl ^{_ n} - ^(pvl ⁺ V vl ),

Pvl _ Yvl - «vl,

_ i_visin(^_vi—^_vi) ABsin(^_vi+p_vi) и ^_               +              .

^vl         sin^ ^i             sin^ ^i

Из тригонометрии известно, что

Sin(^ vl — V vl ) =

_ sin^_vlcosy_vl — cos^_Vlsinv_Vl, sin(^ vl + P vl ) _

_ sin^_vlcosp_vl + cos^_vlsinp_vl.

Путем подстановки выражений (14) в соотношение (13) получаем равенство

0 vl = n-^ vl .

Для определения искомых фазовых сдвигов ^_vl рассмотрим следующее соотношение

АО _ ОС + СА,                      (10)

где отрезок АО является известной величиной и равен модулю V_vk , т. е. АО = V_vl. Теперь необходимо найти выражения, определяющие отрезки ОС и СА. Для нахождения СА будем использовать теорему синусов для треугольника САВ [15]:

CA _ AB sin0vl   sin^vE

Отсюда с учетом (9) и a_vl = ^_vl — v_Vl имеем, что

V vl Sin^ vl _

_ l_Vl(sin^_Vlcosv_Vl — cos^_Vlsinv_Vl) +

+АВ(sin^VlcospVl + cos^vlsinpvl).     (15)

После несложных преобразований на основе равенства (15) можно записать соотношения:

Q vl Sin^ vl = f_vlcosф_vl, v = Т"й,         (16)

где q_vl, f_vl - известные коэффициенты, определяемые формулами:

qvl = АВcospvl — Vvl + IviCOSVvi, fvl = lvlSinVvl —АВsinpvl.

Путем деления левых частей соотношений (16) на cos^_vl Ф 0 получаем следующие уравнения относительно неизвестных фазовых сдвигов ^_vl:

^^^^^^^^^^^^^^^^^^^»

tg(^ vl ) _ ^ Vl , v _ 1,п,                   (17)

^где ^ vl     ^fvl^/qvl "

В результате на основе решений уравнений (17) искомые фазовые сдвиги ^_vl определяются через главные значения arctg(A_Vl) по следующим формулам:

^vl = arctg(A vl ), v = fn.               (18)

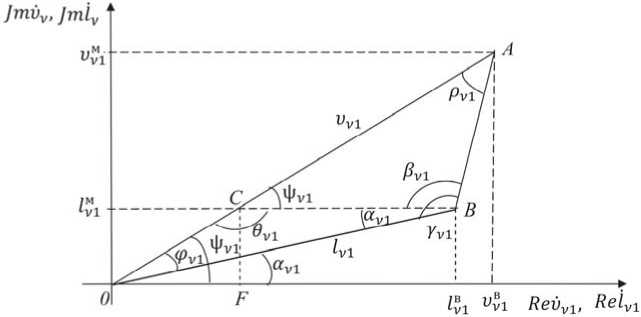
Рис. 3. Геометрическая иллюстрация переменных l _vl и i)_vl

При этом фазовые сдвиги avl определяются выра жениями:

^^^^^^^^^^^^^^^^^^^»

« vl = ^ vl - ^ vl , v = 1,И.

В результате искомые вещественные iVl, U^ и мнимые i-Vl, UVl части комплексных токов ivl и

■                                                                                                                                                            -------------------- напряжений Uvl на нагрузках Zvl (v = 1, и) опре- деляются по следующим формулам:

' vl ^ vl   Wvl Co^ vl ,

' vl ^ vl    ⁱ vl ^ vl ^sin« vl ,

= U^ l = Ut ^i V vi COS^ vI ,

В 'vl м 'vl

В Uvl м Uvl

= U v^l V Vl = U Vl V vl Sin^ vl , v = 1,И.

На основе изложенной методики можно определить и параметры (фазовые сдвиги, вещественные и мнимые части) комплексных токов i_vk и напряжений U_vk на нагрузках Z_vk (v = 1,и, к = 2; 3), подключенных к фазам В и С.

Таким образом, параметры и структура идентификатора динамики нагрузки (ИДН) определяются на основе формул (18)-(20). Реализация ИДН осуществляется программным путем в составе концентратора данных (КД), технически реализуемого на базе микропроцессорной системы.

Оценка переменных состояния магистральной линии трехфазной сети

Использование ИДН позволяет идентифицировать неизмеряемые (неконтролируемые) переменные состояния магистральной линии (МЛ) для любого узла сети на основе законов Кирхгофа, что невозможно на основе действующих значений абонентских токов i_vk и напряжений U_vk (v = 1, и, к = 1,3). Для этой цели рассмотрим функционирование РЭС в отрезке времени [ t 1 , t m ], где 1 1 и t m - начальный и конечный моменты наблюдения соответственно. Процесс измерения необходимых данных счетчиками электроэнергии, их передача по каналу связи (ТКМ) и обработка в концентраторе (КД) осуществляется циклически в интервалах времени [t ^ ,t ^ _+l] (f = 1,m — 1). При этом в каждом цикле моделирования [t ^ ,t ^ _+l] искомые компоненты векторов i_k = [i_lk, i_2k, —, i_n-l , _k] и / = [/_l,/₂, -,/_n-l] с учетом (3) и (19) определяют -ся по следующим выражениям:

ivk = E”=viXk = E”=v(iJk + 7iXk) = ivk + 7%, v = ln, к = 1)3,(21)

jv = ivl + iv2 + iv3, v = 1И,(22)

где в и в ум Vй V ivk ^X=v 'Xk, ivk ^X=v 'Xk,

Л - номер электрического контура сети.

Полученные выше результаты позволяют определить мгновенные токи i_vk(t) и j_v(t), протекающие в межабонентских участках МЛ:

ivk(t) = i“kxsin(wt + ^vk), v = In, к = 13, jv(t) = /v“axsin(wt + 5V), v = In, где амплитуды i™x, /vmax и фазы ^vk, 9v соответ- ствующих переменных состояния находятся на основе вещественных iVk и мнимых iVMk частей, определяемых формулами (23).

Теперь рассмотрим задачу идентификации компонентов векторов напряжений u_k и u, описывающих состояния межабонентских участков МЛ. Напряжения u_vk и O_v в v -х контурах сети удовлетворяют второму закону Кирхгофа [13]:

O vk +_u_v + U vk — U v-l,k = 0,

^^^^^^^^^^^^^^^^^»

v = 1,n, к = 1,3. (24) Напряжения Ov на участках нейтрального провода с учетом (22) и ivk = Ovk/zvk можно записать в виде

^O V    ^jv^zv   ⁽ⁱ vl ^{+ i} V2 ^{+ i} V3 ^)z V

/ ^Vl + йу₂ +

ZV1    ZV2

ZV3

Отсюда при одинаковых сечениях фазных и нейтрального проводов рассматриваемой сети, что эквивалентно равенству соответствующих сопротивлений (zvl = zv2 = zv3 = zv), для напряжений Ov справедливы следующие выражения:

O v = O vl + O v2 + O v3 = o V + ]O V , v = 1, n. (25) С учетом (25) соотношения (24) можно представить в виде систем линейных алгебраических уравнений относительно искомых напряжений o_vk [16]:

2O vl + O v2 + O v3 = b vl ,

^O Vl ^{+ 2O} v2 ^{+ O} V3 = ^b v2 ,                   ⁽²⁶⁾

OVl + OV2 + 2OV3   bV3, v   1, И, к I3, где bvk - известные комплексные коэффициенты, вычисляемые на основе ранее определенных составляющих комплексных напряжений Uvk:

bvl = Uv-l,l — Uvl = bvBl +;bVl, bv2 = U-l,2 — U2 = b^ +;bV2, bv3 = Uv-l,3 — Uv3 = M +7^.

При этом вещественные и мнимые части этих коэффициентов определяются по следующим формулам:

В — Г/В         в     V _ Г/VV bvl = Uv-l,l   Uvl,  bvl = Uv-l,l в _ rp        в    v _ 1]мv bV2 = UV-l,2   UV2, bV2 = UV-l,2

В — Г/В         В     V _ TJVV bV3 = UV-l,3   Uv3, bV3 = UV-l,3

Легко видеть, что определители систем уравнений (26) отличны от нуля (Д = 4), следовательно, они имеют единственные решения, которые можно записать в явном виде:

O vl = (3b vl — b v2 — b v3 )/4,

O v2 = (—b vl + 3b v2 — b v3 )/4,     ___ (27)

O v3 = (—b vl — b v2 + 3b v3 )/4, v = 1,n.

Комплексные напряжения ov на соответствующих участках нейтрального провода находятся путем подстановки найденных напряжений ovl, uv2,uv3 в правые части соотношений (25). При этом их вещественные и мнимые частивычисляют-ся по формулам:

oV = oVl + UV2 + UV3, oV = °Vl + oV2 + oV3.                    (28)

Результаты идентификации текущего состояния РЭС можно использовать для оценки технических потерь электроэнергии в трехфазной сети и текущих значений сопротивлений участков магистральной линии. В случае, когда распределительная сеть функционирует в нормальном режиме, общие технические потери мощности Р (f) в сети в ^-м цикле наблюдения составляют [16]:

P(f) = P o (f) + P i (f), (29) где Р_о (f ) - потери мощности в нейтральном проводе; P₁(f) - суммарные потери мощности в линейных проводах фаз. При этом

Р о (f) = ю P v (f) = M u v (f)k (f), (30) где p_v(f) - потери мощности в v -м участке нейтрального провода; U V (f) - сопряженные значения комплексных напряжений u_v , определяемых формулами (25) и (28); /_v(f) - комплексные токи, протекающие в v -м участке нейтрального провода, определяемые формулами (22).

Потери мощности в линейных проводах фаз определяются формулой

P i (f) = Z l=i 2 ^:1 P v _k(f)=

Оценки текущих значений комплексных сопротивлений zvk = zv межабонентских участков РЭС определяются на основе закона Ома:

2_V k ^ vk /^ vk , ^v 1, ^и, ^к 1,3. ⁽³²⁾

Оценки сопротивлений, приведенные в формулах (32), позволяют определить уровень износа проводов соответствующих участков магистральной линии РЭС и качество контактных соединений.

В результате обобщенный алгоритм моделирования распределительной сети включает следующие основные этапы:

• 1.    Задание структуры распределительной трехфазной сети (например, как на рис. 1).

• 2.    Получение данных о действительных значениях токов I_vk , напряжений U_vk (v = 0, и, к = 1,3) и соответствующих коэффициентов мощности cos^_vk со счетчиков электроэнергии (C4_vk), установленных у абонентов сети и на выходе трансформаторной подстанции.

• 3.    Синтез идентификаторов динамики нагрузок (ИДН) на основе формул (17)–(20).

• 4.    Оценка вещественных и мнимых частей комплексных токов 7_vk и напряжений U_vk(v = 1, и, к = 1,3) на нагрузках Z_vk (v = 1, и, к = 1,3) с использованием ИДН на основе формул (17)–(20).

• 5.    Оценка компонентов i_vk и /_v комплексных векторных токов 1_к и /_v (v = 1,и, к = 1,3), проте-

• кающих в межабонентских участках магистральной линии трехфазной сети, по формулам (21)–(23).

• 6.    Оценка компонентов u_vk и u_v комплексных напряжений й_к и u_v (v = 1,и, к = 1,3) на межабонентских участках магистральной линии трехфазной сети с использованием формул (25)–(28).

• 7.    Оценка технических потерь мощности P(f) в сети по формулам (29)–(31).

Заключение

Рассмотрена проблема моделирования и мониторинга состояния трехфазной распределительной электрической сети (РЭС) напряжением 0,4 кВ в составе АСКУЭ. Предложен метод идентификации недоступных для измерения и контроля токов и напряжений, определяющих электрическое состояние межабонентских участков (МАУ) магистральной линии в режиме реального времени. Считается, что РЭС функционирует в несимметричном режиме, а текущие значения сопротивлений МАУ являются неизвестными величинами. Основная идея метода основана на концепции восстановления переменных, описывающих установившиеся процессы в электроприемниках абонентов сети с использованием данных, полученных со счетчиков электроэнергии по каналам связи. Ее реализация осуществляется на базе специального преобразователя – вычислительного модуля, названного идентификатором динамики нагрузки (ИДН). Предложенный метод дает возможность упростить процедуру моделирования распределительных сетей и позволяет преодолеть недостатки известных методов расчета трехфазных сетей при не-симметрии токов и напряжений.

Полученные результаты ориентированы для создания алгоритмического и специального программного обеспечения подсистемы моделирования и мониторинга электрического состояния РЭС в составе АСКУЭ. Они могут найти применение также для решения задач диагностики и оптимизации режимов работ распределительных сетей.