К проблеме определения параметров распределительной сети по данным АИИС КУЭ
Автор: Данилов Максим Иванович, Романенко Ирина Геннадьевна
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Электроэнергетика
Статья в выпуске: 2 т.20, 2020 года.
Бесплатный доступ
Рассматривается вопрос идентификации параметров четырехпроводной трехфазной распределительной электрической сети (РЭС) напряжением 0,4 кВ по данным векторов тока и напряжения, измеренных автоматизированной информационно-измерительной системой контроля и учета электроэнергии (АИИС КУЭ) в начале РЭС и у каждого ее абонента. Проведен анализ предложенного ранее метода идентификации параметров (сопротивлений) межабонентских участков РЭС, который базируется на модели физических процессов в электрических контурах сети и эквивалентных преобразованиях ее схемы замещения. Показано, что предлагаемые указанные преобразования не являются эквивалентными. При этом найденные сопротивления соответствуют фазным сопротивлениям межабонентских участков при условии равенства нулю сопротивлений нейтрального провода в РЭС и не равны фактическим сопротивлениям четырехпроводной сети. Представлен новый метод решения указанной задачи, основанный на оперативном измерении векторов тока и напряжения в двух разных режимах работы РЭС. Если текущий режим в сети не меняется, то для создания второго (отличающегося от текущего) может применяться однократное временное отключение одного из абонентов РЭС по команде от головного устройства АИИС КУЭ. Полученные результаты могут быть полезны при разработке подсистем АИИС КУЭ, выполняющих функции диагностики и контроля электрического состояния участков магистральной линии распределительной сети, а также оперативного мониторинга в ней коммерческих и технических потерь электроэнергии.
Четырехпроводная распределительная сеть, трехфазная цепь, параметры сети, метод идентификации, диагностика линии
Короткий адрес: https://sciup.org/147234054
IDR: 147234054 | УДК: 620.9:681.011.56 | DOI: 10.14529/power200201
Текст научной статьи К проблеме определения параметров распределительной сети по данным АИИС КУЭ
Вопрос идентификации параметров схемы замещения распределительной электрической сети (РЭС) на основе получаемых данных от автоматизированной информационно-измерительной системы контроля и учета электроэнергии (АИИС КУЭ) рассматривался в ряде работ [1–5]. При этом в работах [1, 4] параметры РЭС определялись на основе данных синхронных векторных измерений тока и напряжения [6–10], которые выполнялись экспериментальными интеллектуальными электронными устройствами (ИЭУ), изготовленными АО «Энергомера» и установленными в начале контролируемого участка РЭС и у каждого зарегистрированного в ней абонента. Предложенная в [1] методика идентификации параметров РЭС основана на применении метода наименьших квадратов, с помощью которого проводится статистическая обработка избыточных данных множества режимов РЭС. При этом проводилось исследование однолинейной четырехпроводной схемы РЭС напряжением 0,4 кВ, для которой считалось, что параметры схемы замещения всех ее фаз одинаковы, а режим работы симметричный. Отметим, что при указанных условиях токи нейтральных проводов на всех участках РЭС будут равны нулю, а, следовательно, в этом случае не будут учитываться со- противления нейтральных проводов, т. е. их сопротивления принимаются равными нулю. В работе [4] методика, предложенная в [1], получила развитие для сетей среднего напряжения 10 кВ, которые являются трехпроводными и выполняются без нулевого провода. Проводился учет наличия в сети трансформаторов тока и напряжения и осуществлялась обработка статистических данных режимов работы РЭС, вследствие чего достигалась компенсация систематических погрешностей ИЭУ (счетчиков электроэнергии) и указанных трансформаторов.
В работах [2, 3, 5] параметры четырехпроводной трехфазной РЭС предлагается определять имеющимися средствами АИИС КУЭ, которые выполняют одновременные измерения для одного и того же интервала наблюдения действующих значений тока и напряжения, а также угла сдвига фаз между ними. Отметим, что в [2] представлена методика, которая рассматривает случай равенства сопротивлений линейных (фазных) проводов между собой и отличие их от сопротивления нейтрального провода. В работе [3] считается, что сопротивления различны для всех фазных и нейтрального проводов. При этом в [2, 3] переход к комплексному представлению измеренных токов и напряжений, т. е. к их векторам, осуществляется согласно описанной в [11, 12] методике. В [5] рас- сматривается случай равенства сопротивлений всех фазных и нейтрального проводов и демонстрируется неработоспособность методики получения векторов из [11, 12]. Важно отметить, что необходимость оперативной, проводимой в режиме реального времени идентификации параметров РЭС обусловлена возможностью изменения их значений в зависимости от внешних условий (температура, влажность). Оперативные данные об указанных параметрах позволят расширить функции существующих АИИС КУЭ в части контроля и диагностики технического состояния и уровня надежности РЭС [13, 14]. Кроме того, важным приложением оперативной оценки параметров РЭС является возможность их использования при реализации существующих и разработке новых методов выявления несанкционированных отборов электроэнергии (НОЭ) на контролируемом участке сети [15–27], а также при идентификации и мониторинге технических и коммерческих потерь электроэнергии в РЭС [15]. Поэтому вопрос оперативной идентификации параметров участков распределительной сети по данным АИИС КУЭ является актуальным и требует своего развития. Отметим, что авторы зарубежных работ системы, подобные АИИС КУЭ, называют Smart-Grid, в их состав входят дистанционно взаимодействующие интеллектуальные счетчики электроэнергии.
В настоящей работе представлен анализ предлагаемого в [3] метода идентификации параметров четырехпроводной РЭС, в котором на основе известных векторов тока и напряжения в распределительной сети определяются сопротивления межабонентских участков магистральной линии при условии разных сопротивлений фазных и нейтральных проводов. При этом показаны его недостатки, приводящие к ошибочным результатам, и предложен новый метод, позволяющий преодолеть указанные трудности (отмеченные недостатки) и получить достоверные результаты.
Постановка задачи
Рассматривается трехфазная четырехпроводная распределительная сеть напряжением 0,4 кВ с установленной АИИС КУЭ (рис. 1). С целью упрощения описания элементов на рис. 1 символом f обозначим фазы А,В,С электрической сети (f = А, В, С). На входе контролируемого участка РЭС подключается головной счетчик электроэнергии (ГСЭ) WQ, у абонентов, зарегистрированных в сети, - счетчики электроэнергии (СЭА) w/, ..., Wi’. Индексом тг обозначается количество абонентов сети, подключаемых к соответствующим фазам сети f . Счетчики электроэнергии W.,. . ., W„ (f = А, В, С) выполняют измерительные функции и дистанционно взаимодействуют с W o , в котором кроме измерений осуществляется обработка данных по предлагаемым вычислительным алгоритмам.
Другие обозначения: Ё^ - трехфазная система питающих ЭДС, представленная в комплексном виде; zQ, .,zQ_1 - комплексные сопротивления фазных и нейтрального z O , .,z „_ t проводов межабонентских участков магистральной линии; Zq ,.. ,Z ^ - нагрузки абонентов фаз сети f.
Далее примем следующие допущения.
-
1. Распределительная сеть в рассматриваемом интервале времени функционирует в нормальном (безаварийном) режиме, и все ее элементы являются линейными.
-
2. Сопротивления фазных и нейтральных проводов v -х межабонентских участков РЭС считаются неизвестными и имеющими различные значения как в пределах одного и того же v -го межабонентского участка, т. е.
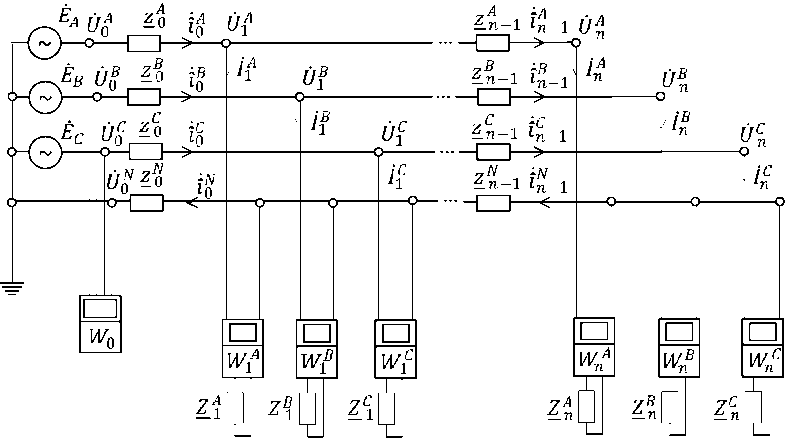
Рис. 1. Расчетная схема участка четырехпроводной распределительной сети, в которой установлена АИИС КУЭ
-
3. Всеми счетчиками АИИС КУЭ в рассматриваемом интервале наблюдения проводятся синхронные векторные измерения напряжений и токов. В результате для каждого периода питающего напряжения становятся известными для всех фаз сети f комплексы токов и напряжений в начале контролируемого участка РЭС: Iq , Uy , а также у каждого соответствующего v -го потребителя (абонента) электроэнергии: 4 , 4 , (v = 1, п, = =А,В,Су По каналам связи указанные данные передаются от СЭА в ГСЭ, в котором формируются комплексные векторы токов / у = [/ q , ■ ■■,/ „ ] и напряжений U у = [ Uq, ..., Uy] для периодов питающих напряжений, где /У = Де 'А, Uy = Uye^” - комплексные токи и напряжения в РЭС (v = 0, n, f = А , В , С). При этом фазовые сдвиги «у, 4 для трехфазной распределительной сети представим так:
Zy * z^, z^ * z^, z^ * z®, zy * zy, f = А,В, C, v = 0,n — 1, так и любых других (v + i)-х межабонентских участков, т. е. в РЭС все сопротивления имеют различные значения:
_у * tzo * zy+i * Ло + 1, f = А,B , C, v = 0,n — 1, где индекс i - численная переменная i = 0, n — 1, позволяющая выбирать для сравнения сопротивления на любом, кроме рассматриваемого v-го, межабонентском участке.
-
4 = 4 — «Ь 4 = 4~ 4 ,
v = 0, n, f = А,В, С, а1 = 4 = 0, (1)
й в =4 = —2тг/3, а В = ф в = 2л/3, где , - приращение фазовых сдвигов относительно их номинальных значений в, в,
=А,В, С .
Задача заключается в том, чтобы на основе указанных измеренных данных токов / у и напряжений U ^ определить элементы матрицы Z, которая состоит из комплексных сопротивлений всех фазных 4 = Zye' … Теоретическая часть Решение сформулированной задачи рассматривалось в работе [3], в которой предлагается для соответствующего v-го межабонентского участка магистральной линии фаз сети использовать следующую систему уравнений: ̇ ̇ ̇ ̇ lyzy + 1 yzy U V +1 U у, ̇ ̇ ̇̇ lyzy + ly zy Uy Uy +1, ̇ ̇ ̇̇ + 1 y zy Uy Uy +1, aM аД I AD ." Ap __ ZA ly = ly + ly+ ly, v = 0,П - 1. Очевидно, что такая система является несвязной и найти из нее четыре неизвестных z®, z®, z® и 4 не удастся. Авторы [3] предлагают представить ток нейтрального провода iy следующим образом: ̇ ̇ ̇ ly fA_„N + fB_„N + fC_,N , (3) ) V ) V ±-V ) v v = 0, n — 1, где 4 = Uy — Uy+1, fy = zy + zУ, (f = А,B , C). Отметим, что введенные в уравнение токов нейтрального провода ly обозначения by и fy не добавляют в систему (2) требуемой для ее решения информации. В работе [3] считается, что найти f у можно, э используя эквивалентные сопротивления , для этого записываются выражения: э э -y f +Zэ ” +Z”, (4) v = 1,n — 1, f = А,В, С, где Z_4 = 4/iy_i, 4 = Uy/iy, -иУ=^/'и (рис. 2а), —®у = Zу. Определим эквивалентное сопротивление относительного первого ( v = 1) и второго ( = 2) абонентов соответствующих фаз сети (рис. 2б, в): ZV = 4 /?о, Z ээ у = и^У/^У, f = АВс. При этом выражения (4) примут следующий вид: э ЙУ = А; V• ? = А,В,с• (5) где fУ = zy + zy. Очевидно (см. рис. 2), что выражения (4) и (5) не учитывают наличие узлов, образованных нагрузками абонентов фаз сети, из-за которых со-э противления zy, zy, — не являются включен ными последовательно и поэтому их нельзя складывать: zy + zy + — ®y y, v = 0, n — 1, f = А, В, C. В результате выполняемого выше сложения а) б) в) Рис. 2. Эквивалентные преобразования сопротивлений в четырехпроводной распределительной сети находятся эквивалентные сопротивления v-х межабонентских участков фаз сети f (см. рис. 2б): ̂̇ ̇ ̇ £p zp + a? zp а? , v = 0,п - 1, f = А, В, С. В таком случае сопротивления нулевого провода принимаются равными нулю, т. е. в работе [3] найдены z^, z®, z1^ при условии z” = 0, где z” -сопротивление нулевого провода в эквивалентной схеме РЭС. Таким образом, не удастся найти элементы матрицы 2, вследствие этого предложенная в [3] методика не позволяет решить сформулированную задачу. Предлагаемый метод. Рассмотрим нулевой контур (v = 0) РЭС (рис. 2б) при условиях zA * z®, zA * z® , z® * z® , z^ * z” и эквивалентных сопротивлениях Z®Q (f = А, В, С). В представленном случае невозможно однозначно определить сопротивления трех фазных и одного нейтрального проводов, используя данные Uq , U^, Iq, i” только одного режима РЭС. Однако считая, что параметры zQ и z” (f = А, В, С) не зависят от режима в РЭС, выполнив измерения при другом режиме, получим дополнительные данные U'q , U'q, i'Q, i'”, которые можно использовать для нахождения параметров zQ и z” (f = А, В, С). При этом требуется, чтобы параметры zQ и z” (f = А, В, С), зависящие от внешних факторов (температура, влажность), не успели измениться за время, необходимое для появления нового режима в РЭС и измерения его данных U'Q, U'Q , i‘Q, i‘”. Таким образом, для работы предлагаемой методики необходимы измерения в двух различных режимах работы сети, отстоящих друг от друга не менее 0,1 с для исключения влияния переходных режимов и не более 1,0 с, чтобы параметры РЭС не успели измениться. Анализ режимов в РЭС выполняет ГСЭ путем контроля изменения питающего напряжения и/или мощности, потребляемой абонентами. Если текущий режим в сети не меняется, то для создания второго (отличающегося от текущего) ГСЭ может подать команду временно отключить одного из абонентов РЭС, создав (задав) тем самым второй режим, и затем выполнить запрос информации со счетчиков абонентов. Таким образом, ГСЭ может запрашивать информацию со счетчиков не периодически с заданной частотой, а по необходимости при изменении режима в РЭС. Если режим не изменяется, то и ранее найденные параметры не меняются. В случае если режимы в РЭС изменяются быстро, то для мониторинга состояния сети запрашивать необходимые данные со счетчиков можно один раз в 10–15 мин, что не вызовет перегрузку систем связи. Запишем систему уравнений для определения параметров zQ, z” (f = А, В, С): qq n„n _ rA _ rA 1о_о + l0z0 = U0 U1 , ti + i'NzN = и'о - U'q , (6) f = авс, где i'” = i'^1 + i'® + i'g. Система (6) состоит из шести уравнений с четырьмя неизвестными. Выбрав произвольные четыре уравнения из (6), например, три уравнения первого режима и одно уравнение второго режима, записанное для фазы А: fА7А ”7” f,A f,A , lvzp + lp zp Up Uv+1, ̇̇̇̇ lpzp + lp£p Up Up + 1, (7) ^7C ”7” fC_nC_. lpzp + lp zp Up Up+1, ^A7A iN7N - 7?a - 7?a . 1 pzp + 1 p zp U p U p+1, v = 0,n - 1, определим Zp и Ли (V=0,n-1, f = ,В,C), а следовательно, и искомую матрицу 2. Отметим, что определить параметры РЭС возможно, если по ним протекают токи. Поэтому в случае формирования режимов в РЭС путем отключения нагрузки отдельных абонентов необходимо следить за тем, чтобы токи межабонентских участков при этом не оказывались равными нулю. Практическая часть Представим пример расчета параметров межабонентских участков четырёхпроводной распределительной сети (см. рис. 1) в случае трех (и=3) ответвлений абонентов на каждую из фаз f= ,в,c. Выделим три этапа: 1. Зададим исходные данные (табл. 1) и проведем расчет для двух режимов работы РЭС. 2. Используя данные п. 1, согласно уравнениям методики [3] рассчитаем сопротивления первого межабонентского участка РЭС z^ (V=1, f= ,В,c). 3. Используя полученные в п. 1 данные, согласно предлагаемому методу уравнения (7), проведем расчет матрицы 2. Первый этап Зададим комплексы питающих напряжений фаз сети f так: ̇A=220ei0 (В), İB =220e("2" ⁄3)1 (В), ̇ 'c =220e(2"⁄3)1 (В). Для расчетов используем данные нагрузок абонентов РЭС (см. табл. 1), которые заданы произвольным образом, создавая несимметричный режим работы сети. Элементы матрицы 2 (см. табл. 1), которые представляют собой комплексные сопротивления фазных Zp и нейтрального Ли проводников межабонентских участков, зададим как: Ли =(kT )J[Re(Z)+j(кф )V Im(Z)], V = 0,2, f= ,В,C,N, где кД , ^фу – коэффициенты, заданные произвольным образом (см. табл. 1), которые используются для формирования элементов матрицы 2с помощью исходного комплексного сопротивления z = (0,0012 + j0,000192) Ом, соответствующего трем метрам одножильного кабеля 5АПВ 1х70 [5]. Расчет режимов РЭС при помощи метода узловых напряжений проводился в Mathcad. Результаты расчетов представлены в табл. 2, 3. Первый режим РЭС (см. табл. 2) соответствует исходным данным нагрузок абонентов (см. табл. 1). Второй – при отключенном абоненте: =∞. Фазовые уг лы в табл. 2, 3 записаны с учетом выражений (1). Второй этап Используя данные табл. 2, согласно методике [3] уравнениям (2)–(5), были рассчитаны сопротивления z^ (v=1, f= ,В,c,) первого межабо нентского участка РЭС (см. рис. 2в). Получены следующие результаты: для фазы A – модуль Z1 = 0,001462 Ом, аргумент Фгг=- 4,7590724 эл. град; для фазы В – модуль zf = 0,001141 Ом, аргумент Фгг = 38,9988061 эл. град; для фазы С – модуль zf = 0,001015 Ом, аргумент Фгг=- 89,5071763 эл. град; для N – модуль Z1 и аргумент Фгг оказались равными нулю. Отметим, что полученные результаты расчетов согласуются с теоретической частью, где от- Таблица 1 Исходные данные для расчета режимов РЭС Абоненты фаз сети Модули Z и начальные фазы ф сопротивлений нагрузки абонентов Комплексные сопротивления элементов матрицы 2 | № абонента Фаза сети , Ом ф, эл. град соѕ (ф) , Ом КГр Z = 0,00120+j0,0001920 1 л 6,875 66,4218215 0,400 1,10 1,5 7А 0,00132 + j0,0003168 в 5,5 11,4783400 0,980 1,15 1,0 7В 0,00138 + j0,0002208 с 55,0 45,0000000 0,707 1,05 0,5 7С 0,00126 + j0,0001008 1,0 1,5 £о 0,00120 + j0,0002880 2 л 5,5 45,0000000 0,707 0,90 1,0 7А 0,00108 + j0,0001728 в 11,0 66,4218215 0,400 0,85 1,0 7В 0,00102 + j0,0001632 с 44,0 66,4218215 0,400 1,20 1,5 0,00144 + j0,0003456 0,95 0,5 0,00114 + j0,0000912 3 л 10,0 45,0000000 0,707 0,80 1,5 7А £2 0,00096 + j0,0002304 в 6,875 66,4218215 0,400 0,75 0,5 7В £2 0,00090 + j0,0000720 с 22,0 66,4218215 0,400 1,25 1,0 7С £2 0,00150 + j0,000240 1,30 1,0 7N £2 0,00156 + j0,0002496 Таблица 2 Результаты расчетов первого режима РЭС Абоненты фаз сети Модули и фазы расчетных значений токов и напряжений абонентов № абонента Фаза сети U, В Ф, эл. град I, А a, эл. град 1 A 219,892470 0,0467212 31,984359 –66,3751003 В 219,822500 0,0012142 39,967727 –11,4771268 C 220,079343 –0,0057414 4,001443 –45,0057414 2 A 219,833935 0,0647387 39,969806 –44,9352613 В 219,769903 0,0083256 19,979082 293,5865040 C 220,093249 –0,0041242 5,002119 –66,4259458 3 A 219,830469 0,0699473 21,983047 –44,9300527 В 219,741272 0,0172242 31,962367 293,5954027 C 220,085034 –0,0053095 10,003865 –66,4271310 Таблица 3 Результаты расчетов второго режима РЭС Абоненты фаз сети Модули и фазы расчетных значений токов и напряжений абонентов № абонента Фаза сети U, В Ф, эл. град I, А a, эл. град 1 A 219,980774 0,0326630 31,997204 –66,3891586 В 219,823658 0,0140439 39,967938 –11,4642971 C 220,036113 –0,0118901 4,000657 –45,0118901 2 A 219,992440 0,0362952 0 0 В 219,779242 0,0328698 19,979931 293,611048 C 220,007025 –0,0142830 5,000160 –66,436105 3 A 219,988948 0,0415190 21,998895 –44,958481 В 219,750569 0,0417607 31,963720 293,619939 C 219,998871 –0,0154755 9,999949 –66,437297 Таблица 4 Расчетные значения элементов матрицы 2 A f делить эквивалентные сопротивления первых ̂ 1 межабонентских участков фаз сети f . Таким образом, результатами расчетов подтверждается невозможность найти достоверные элементы матрицы 2, используя предложенную в [3] методику. Третий этап На̂̇ f ̇N ̇ £ ̇N основе комплексов токов ̂P, ̂P , ̂′P , ̂′Pи напряжений ̇ P, ̇P,İ′P,İ′P абонентов V = 0,2, f= ,В,c, взятых из табл. 2, 3, был выполнен расчет по уравнениям (7). В результате получены элементы матрицы 2, которые представлены в табл. 4 в виде модулей ̌ и аргументов Ф ̌. Таким образом, предлагаемый в настоящей работе метод, представляющий собой систему уравнений (7), позволяет найти элементы матрицы z и получить значения сопротивлений фазных и нейтральных проводов межабонентских участков РЭС, соответствующие фактическим. Заключение Рассмотрена проблема идентификации параметров четырехпроводной трехфазной распределительной сети напряжением 0,4 кВ на основе данных векторных измерений токов и напряжений, выполняемых в начале РЭС и у каждого ее абонента в случае, если все сопротивления проводов межабонентских участков различны. Проведен анализ предложенного ранее в [3] «метода идентификации параметров (сопротивлений) на основе модели физических процессов в электрических контурах сети и оценки недоступных для измерения и контроля переменных, описывающих текущее электрическое состояние межабонентских участков трехфазной сети», в котором решалась указанная задача. В результате выявлены его недостатки и теоретически обоснована невозможность решить сформулированную задачу предлагаемым методом. Показано, что методом, представленным в работе [3], находятся эквивалентные фазные сопротивления межабонентских участков, т. е. те, которые определяются при условии равенства нулю сопротивлений нейтрального провода в РЭС. Проведенный согласно теоретическому обоснованию расчет подтвердил равенство нулю сопротивления нейтрального провода и по- казал соответствие получаемых сопротивлений эквивалентным. Предложен новый метод идентификации параметров четырехпроводной трехфазной распределительной сети при условии, что все сопротивления проводов межабонентских участков РЭС различны. Метод основан на оперативном измерении векторов тока и напряжения в двух разных режимах работы РЭС, которые при необходимости могут задаваться АИИС КУЭ. Полученные результаты полезны для развития функциональных возможностей АИИС КУЭ в части создания подсистем диагностики и контроля функционального состояния участков магистральной линии распределительной сети, а также при реализации оперативного мониторинга и идентификации коммерческих и технических потерь электроэнергии.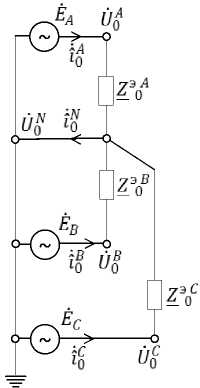
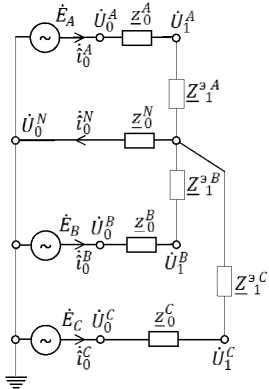
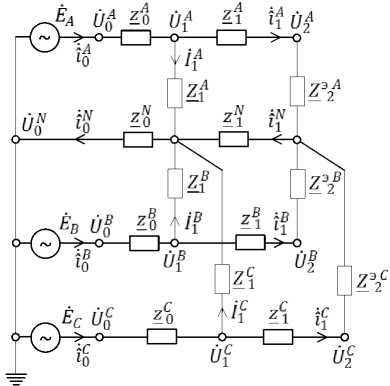
Индексы сопротивлений проводов сети
Номера межабонентских участков
V=0
V=1
V=2
V
̌, Ом
Ф ̌, эл. град
V
̌, Ом
Ф ̌, эл. град
V
̌, Ом
Ф ̌, эл. град
A
0,001357
13,4957333
0,001094
9,0902769
0,000987
13,4957333
В
0,001398
9,0902769
0,001033
9,0902769
0,000903
4,5739213
C
0,001264
4,5739213
0,001481
13,4957333
0,001519
9,0902769
N
0,001234
13,4957333
0,001144
4,5739214
0,001580
9,0902769
мечается, что согласно методике [3] можно опре-
Список литературы К проблеме определения параметров распределительной сети по данным АИИС КУЭ
- Zelenskii, E.G. Identification of the parameters of distribution networks by synchronized current and voltage measurements / E.G. Zelenskii, Y.G. Kononov, I.I. Levchenko // Russian Electrical Engineering. - 2016. -Vol. 87, no. 7. - P. 363-368. DOI: 10.3103/S1068371216070129
- Оморов, Т.Т. Определение параметров распределительных сетей 0,4 кВ по данным АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев, Р. Ч. Осмонова // Энергетик. - 2017. - № 6. - C. 3 7-40.
- Оморов, Т.Т. Параметрическая идентификация распределительной сети в составе АСКУЭ / Т.Т. Оморов, Р.Ч. Осмонова, Т.Ж. Койбагаров // Вестник ЮУрГУ. Серия «Энергетика». - 2018. - Т. 18, № 1. - С. 46-52. DOI: 10.14529/power180106
- Кононов, Ю.Г. Уточнение параметров участков линий сети среднего напряжения по данным синхронных измерений / Ю.Г. Кононов, О.С. Рыбасова, В.С. Михайленко // Известия высших учебных заведений. Электромеханика. - 2018. - Т. 61, № 1. - С. 77-84.
- Данилов, М.И. К проблеме определения векторов тока и напряжения в распределительной сети по данным АИИС КУЭ / М.И. Данилов, И.Г. Романенко // Вестник ЮУрГУ. Серия «Энергетика». - 2019. -Т. 19, № 4. - С. 87-94. DOI: 10.14529/power190410
- IEEE Standard for Synchrophasor Measurements for Power Systems, [IEEE Std C37.118.1-2011 (Revision of IEEE Std C37.118-2005)], Dec. 28, 2011.
- Wu, Z. [Simultaneous transmission line parameter and PMU measurement calibration] / Z. Wu, L.T. Zora, A.G. Phadke // IEEE Power & Energy Society General Meeting, Denver. - 2015. - P. 1-5. DOI: 10.1109/PESGM.2015.7286115
- A Novel Approach to Noninvasive Measurement of Overhead Line Impedance Parameters / D. Ritzmann, J. Rens, P.S. Wright et al. // IEEE Transactions on Instrumentation and Measurement. - 2017. - Vol. 66. -P. 1155-1163. DOI: 10.1109/TIM.2017.2665958
- Пат. 2619134 РФ, G01R 19/00. Способ синхронизации измерений в электрических сетях по частоте и фазе напряжения силовой сети / Ю.Г. Кононов, П.А. Звада; заявитель и патентообладатель СевероКавказский федерал. ун-т. - № 2015151889, заявл. 03.12.2015; опубл. 12.05.2017, Бюл. № 14. - 2 с.: ил.
- Compensation of Systematic Measurement Errors in a PMU-Based Monitoring System for Electric Distribution Grids / P.A. Pegoraro, K. Brady, P. Castello et al. //IEEE Transactions on Instrumentation and Measurement. - 2019. - Vol. 68. - P. 3871-3882. DOI: 10.1109/TIM.2019.2908703
- Оморов, Т.Т. К проблеме моделирования несимметричных распределительных электрических сетей в составе АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев, Р. Ч. Осмонова // Вестник ЮУрГУ. Серия «Энергетика». - 2017. - Т. 17, № 1. - С. 21-28. DOI: 10.14529/power170103
- Оморов, Т.Т. К расчету трехфазных распределительных сетей в системах автоматизации контроля и учета электроэнергии / Т. Т. Оморов, Б.К. Такырбашев, Р. Ч. Осмонова // Энергетик. - 2017. - № 4. -C. 28-31.
- Rejc, Z.B. Estimating the additional operating reserve in power systems with installed renewable energy sources / Z.B. Rejc, M. Cepin // International Journal of Electrical Power & Energy Systems. - 2014. - Vol. 62. -P. 654-664.
- Power System Reliability Importance Measures /M. Cepin, M. Demin, M. Danilov et al. // 29th European Safety and Reliability Conference, Hannover. - 2019. - P.1633-1637. DOI: 10.3850/978-981-11-2724-3_ 0156-cd
- Оморов, Т.Т. Идентификация и мониторинг потерь электроэнергии в распределительной сети в составе АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев //Электричество. - 2016. - № 11. - С. 4—11.
- Electricity Theft Pinpointing through Correlation Analysis of Master and Individual Meter Readings / P. Biswas, H. Cai, B. Zhou et al. //IEEE Transactions on Smart Grid. - 2019. DOI: 10.1109/TSG.2019.2961136
- Messinis, G.M. A Hybrid Method for Non-Technical Loss Detection in Smart Distribution Grids / G.M. Messinis, A.E. Rigas, N.D. Hatziargyriou // IEEE Transactions on Smart Grid. - 2019. - Vol. 10, no. 6. -P. 6080-6091. DOI: 10.1109/TSG.2019.2896381
- Review of various modeling techniques for the detection of electricity theft in smart grid environment / A. Tanveer, C. Huanxin, W. Jiangyu, G. Yabin //Renewable and Sustainable Energy Reviews. - 2018. - Vol. 82. -P. 2916-2933.
- Solutions for detection of non-technical losses in the electricity grid: A review / J.L.Viegas, P.R. Esteves, R. Melicio et al. // Renewable and Sustainable Energy Reviews. - 2017. - Vol. 80. - P. 1256-1268. DOI: 10.1016/j.rser.2017.05.193
- Detection of energy theft and defective smart meters in smart grids using linear regression / S. -C. Yip, K.Sh. Wong, W.-P. Hew et al. // International Journal of Electrical Power & Energy Systems. - 2017. - Vol. 91. -P. 230-240.
- Tanveer, A. Non-technical loss analysis and prevention using smart meters / A. Tanveer // Renewable and Sustainable Energy Reviews. - 2017. - Vol. 72. - P. 573-589.
- Pat. CN 106405276, G01R31/00. Low voltage network electricity theft detection method based on AMI data /L. Wenpeng, Zh. Lei, Y. Yixin et al. - N10737669; Pend. 2016.08.26; Publish. 2017.02.15. - 8p.
- Minimizing non-technical losses with point-to-point measurement of voltage drop between "SMART" meters / I. Bula, V. Hoxha, M. Shala, E. Hajrizi //IFAC-PapersOnLine - 2016. - Vol. 49, iss. 29. - P. 206-211.
- Jokar, P. Electricity Theft Detection in AMI Using Customers' Consumption Patterns / P. Jokar, N. Arianpoo, V. Leung // IEEE Transactions on Smart Grid. - 2015. - Vol. 7, no. 1. - P. 216-226. DOI: 10.1109/TSG. 2015.2425222
- Spiric, J. Fraud detection in registered electricity time series / J. Spiric, M. Docic, S.S. Stankovic //International Journal of ElectricalPower& Energy Systems. - 2015. - Vol. 71. - P. 42-50. DOI: 10.1016/j.ijepes.2015.02.037
- Сапронов, А.А. Оперативное выявление неконтролируемого потребления электроэнергии в электрических сетях напряжением до 1 кВ / А.А. Сапронов, С.Л. Кужеков, В.Г. Тынянский // Изв. вузов. Электромеханика. - 2004. - № 1. - C. 55-58.
- Данилов, М.И. Метод выявления мест неконтролируемого потребления электроэнергии в электрических сетях 0,4 кВ /М.И. Данилов, И.Г. Романенко //Изв. вузов. Электромеханика. - 2019. -Т. 62, № 4. -C. 90-96.


