К проблеме определения векторов тока и напряжения в распределительной сети по данным АИИС КУЭ
Автор: Данилов Максим Иванович, Романенко Ирина Геннадьевна
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Электроэнергетика
Статья в выпуске: 4 т.19, 2019 года.
Бесплатный доступ
Рассматривается вопрос определения векторов тока и напряжения в трехфазной распределительной электрической сети (РЭС) напряжением 0,4 кВ. Считается, что сопротивления межабонентских участков РЭС являются неизвестными вследствие того, что они могут существенным образом зависеть от внешних факторов (температура, влажность и др.). В распределительной сети функционирует автоматизированная информационно-измерительная система контроля и учета электроэнергии (АИИС КУЭ), средствами которой производятся одновременные измерения для одного и того же интервала наблюдения действующих значений тока и напряжения, а также активной и реактивной мощностей в начале РЭС и у каждого ее абонента. Проведен анализ предложенного ранее «метода идентификации недоступных для измерения и контроля токов и напряжений», который базируется на определении векторов тока и напряжения путем синтеза идентификатора динамики нагрузки с использованием относительных величин и констант для их формирования. Показаны его недостатки, и представлен новый метод решения указанной задачи. Полученные результаты могут быть полезны при разработке специального программного обеспечения подсистем мониторинга электрического состояния, реализуемых в составе АИИС КУЭ.
Вектор тока, метод идентификации, распределительная сеть, трехфазная цепь
Короткий адрес: https://sciup.org/147232762
IDR: 147232762 | УДК: 620.9:681.011.56 | DOI: 10.14529/power190410
Текст научной статьи К проблеме определения векторов тока и напряжения в распределительной сети по данным АИИС КУЭ
Вопрос определения векторов тока и напряжения в распределительной электрической сети (РЭС) на основе полученных одновременно за один и тот же интервал наблюдения измерений действующих значений токов и напряжений, а также активных и реактивных мощностей в начале линии и у каждого абонента РЭС, выполняемых автоматизированной информационно-измерительной системой контроля и учета электроэнергии (АИИС КУЭ), рассматривался в ряде работ [1–4]. При этом отмечается возможность получения указанных векторов без использования значений сопротивлений межабонентских участков магистральной линии (МЛ), которые являются неопределенными параметрами, изменяющимися в зависимости от внешних условий (температура, влажность). Таким образом, по мнению авторов, становилось возможным нахождение (идентификация) параметров схемы замещения РЭС, что является очень важным обстоятельством, поскольку может позволить осуществлять оперативную диагностику функционального состояния сети с целью контроля ее уровня надежности [5, 6] и проводить мониторинг потерь электроэнергии в режиме реального времени. В работах [7–10] рассматривается задача определения параметров схемы замещения линий сети с использованием векторов токов и напряжений в РЭС, получаемых от устройств PMU (Phasor Measurement Unit), которые осуществляют синхронные векторные измерения [11, 12]. Отметим, что разработаны и менее затратные способы [13, 14] синхронных векторных измерений. Однако широкое внедрение достижений в области синхронных векторных измерений в АИИС КУЭ на настоящем этапе развития науки и техники затруднительно, так как экономический результат не покрывает их стоимость. Важным приложением определения векторов тока и напряжения в РЭС является их использование для разработки методов обнаружения несанкционированного отбора электроэнергии (НОЭ) – его координат и объема. Вопросу обнаружения НОЭ в РЭС посвящен ряд работ [15–24], в которых отмечается необходимость применения интеллектуальных счетчиков электроэнергии, входящих в состав Smart-Grid. Поэтому вопрос определения векторов тока и напряжения в распределительной сети по данным АИИС КУЭ является актуальным и требует своего развития. Отметим, что необходимость синхронных векторных измерений обусловлена трудностью однозначного определения режима РЭС другими способами.
В представленной нами работе дано теоретическое обоснование и практический расчет, указывающий на неработоспособность предложенной в работе [3] методики определения векторов тока и напряжения в РЭС по данным АИИС КУЭ. Предложен метод, позволяющий преодолеть выявленные недостатки.
Постановка задачи
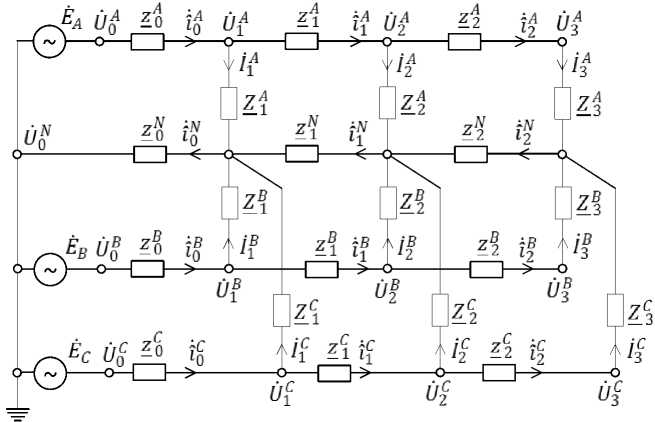
Рассматривается трехфазная распределительная сеть напряжением 0,4 кВ, в которой установлена АИИС КУЭ (рис. 1), состоящая из головного счетчика электроэнергии (ГСЭ) и счетчиков электроэнергии абонентов (СЭА): ,…, ,
,…, , ,…, , где , , – фазы элек трической сети; – числовой индекс, обозначающий количество ответвлений абонентов сети.
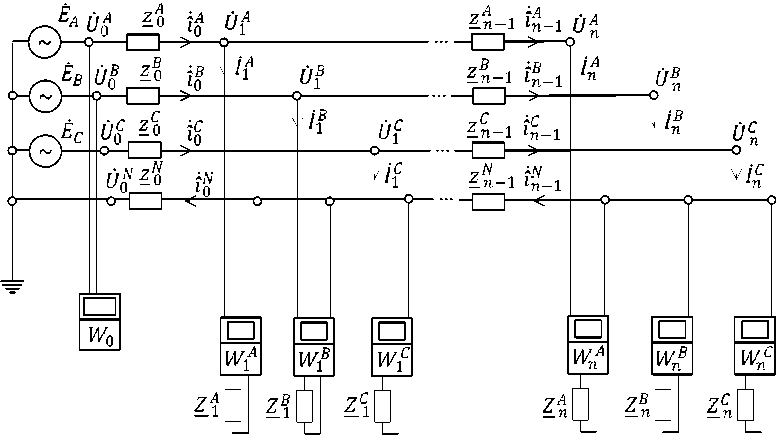
Рис. 1. Схема контролируемого участка трехфазной РЭС с установленной АИИС КУЭ
ГСЭ выполняет измерительные, вычислительные и коммуникационные функции, дистанционно взаимодействуя с СЭА. Остальные обозначения: ЁА, Ёв , Ё с - трехфазная система питающих ЭДС, представленная в комплексном виде; z^, ./z^.^, z®, — ,z ®-y , z Q , ...,£^1, z Q , —,z ^ -1 - комплексные сопротивления межабонентских участков питающей линии; Z o , .„,Z^, Z Q ,.,Z ® , Z_ 0 , — ,Z® - комплексные сопротивления нагрузки абонентов (потребителей).
Приняты следующие допущения.
-
1. В рассматриваемом интервале времени распределительная сеть функционирует в нормальном (безаварийном) несимметричном режиме.
-
2. Каждый из счетчиков по командному сигналу от ГСЭ за интервал времени порядка 0,1 с может измерить активную р®, и реактивную рМ^ мощность, а также действующие значения напряжения Uy, и тока уу, у соответствующего v-го потребителя (абонента) электроэнергии ( v = 1, и) и в начале контролируемого участка: в , м , , ,
-
3. Одновременно измеренные данные СЭА: р ®, , р”, , и^ , 1 У,, (v — 1, п, — = А,В , С) по каналам связи передаются в ГСЭ, где имеются данные: в , Р о, , Uq, , Iq f (f = А,В , С) для того же момента времени.
где - переменная, обозначающая фазы , , рассматриваемой сети.
Задача заключается в том, чтобы на основе указанных измеренных данных определить комплексные векторы токов 1 ,= [I0,, ..., Тп,] и напряжений ̇ = ̇ ,…, ̇ , советующих дейст вующему в РЭС режиму, где Uy, — Uv,е^,, iy, = Iy, e1 “^^ — комплексные напряжения и токи в РЭС (v — 0, и, f — А, В, С). Начальные фазы Уу,, для несимметричной трехфазной сети можно записать следующим образом:
^vA УА уА ,
У уВ = Уув - 2/33,
Фус = У ус + 2^/3, ® уА = ® уА , (1)
аУв = «ув - 2/33, аУс = «ус + 2//3, ___ ______ где (руА — УуА - ауА, v — 1, п, ^ — А,В, С.
Теоретическая часть
Построим векторную диаграмму (рис. 2) тока и напряжения первого абонента ( =1 ) одноименной фазы f сети. Примем U^, — Uo, — Е, (f — А , В, С), т. е. на входе цепи (сети) действуют номинальные симметричные напряжения с модулями = = = , которые измеряются ГСЭ ( ).
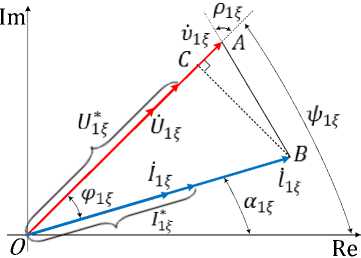
Рис. 2. Представление на комплексной плоскости переменных ̇ , ̇ , ̇ , ̇ , записанных для первых ( = ) абонентов одноименных фаз сети и их связь с ,
Определим согласно [3] I,, следующим образом: I, — U,,/Z,,, где Z,, — и*//,, - модуль комплексного сопротивления первого абонента, известный на основе измерений его напряжения и1? и тока /1? , выполняемых СЭА (WT ? ).
Согласно [3] далее вводятся новые комплексные переменные:
V1? — Ui 1', I 1? —'7 f,f— а,В,с .(2)
Uif'
Так как илГ U3F --------
1^ = 71? — Аf— А,В,С,(3)
'if очевидно, что
V 1? — U 1 L g i^ if = Z1 ? ei^ if ,
I 1? — 'ie = Z^1"1,(4)
' if
V 1? = ^ 1? ,f= А , В , С .
Таким образом, в треугольнике ОАВ (см. рис. 2) сторона ОА равна ОB .
Рассмотрим полученные в [3] коэффициенты 9 1? , / 1? , используемые для нахождения ^1 ? :
9 1? =( АВ )соѕ (Р 1?) - V 1? + ^ 1? соѕ ( ф1? ),
A? = ^ 1? sin(ф 1? )-( АВ )sin (Р 1? ) , (5)
^ 1? = arctg ^— ^) ,f— А, В , С .
Согласно рис. 2 можно записать:
( АВ )соѕ (р1 ? ) = СА ,
7 1? соѕ(ф 1? ) = ОС ,
V 1? = ОА , (6)
7 1? ⁄sin (Р 1? )=(АВ)⁄sin(ф 1? ),f= А , В , С .
Очевидно, что при V 1? — 1 1? (f— А , В , С ) коэффициенты 9 1? , / 1? равны нулю:
9 1? =0, / 1? =0, f — А , В , С . (7)
Таким образом, не удастся найти ^ 1? , а, соответственно, и а1 ? — ^1? - Ф 1? , где Ф 1? — = arctg (р1?/р В ? ) является известным (измеряется СЭА . W ? ). Вследствие этого методика определения комплексных векторов токов и напряжений, представленная в [3], не позволяет решить сформулированную задачу.
Предлагаемый метод . Рассмотрим нулевой контур (V=0) РЭС при условии ^ 0 — Z o — Z ?
(Г _ Г ТВ Г?
(f— А,В,С). Комплексы входного тока
(f— А , В , С ) известны (измеряются ГСЭ):
t?— рв?⁄ и?? +jpм. ?⁄ и?? , t? — I??ej"of, а?? — ^v? - ф?? ,(8)
ф ?? = arctg (рм; / Р в?) .
Тогда запишем напряжения в нулевом контуре (V =0 ) так:
и 1? — и ?? — (t ?+1о )Z? — и ?? — i ? Z? ,(9)
где t N— tA+ tВ+ t^ Z
-
l ? — l ? + l ? + l ? , Z ? — Z ? e u ,
i ? N — t ? + 1 N — l Br + j Iм,
-
l ? — l ? + l ? — 1 ?? + jt ?? ,
-
1 ? N — i ? e^ 0 , f — АГ в ГС .
Тогда согласно (9) неизвестными для нулевого контура (V=0) всех фаз f являются: ^P1A , ^Р1В , ^Р1С , Z? , фг0 . При этом параметры ^1А , ^P1B , ^^1С однозначно определяются через Z? , Фг0 . Поэтому необходимы только два уравнения для нахождения неизвестных.
Для этого запишем (9) для двух произвольных фаз, например, АиВ в виде:
_ UoA _ U i A _ UoB _ U i B
? ? ( i A + i o ) - (i A + io')■ (i 0 + i o ) - ( i 0 + i o ) ,
тогда согласно рис. 3 можно получить систему из двух уравнений с неизвестными Z? , Фх0:
(Z ? ) 2 + ( i ' aw ) 2 — 2 Z ? I AN соѕ (‘фА 0 ) —
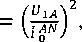
(Z ? ) 2 + (i ' bn ) 2 —2 Z ? I' bn соѕ (‘ P z o ) —
U oB 2
где
5*A 0 — (ccAN + Ф г0 ) ,
^0
— (ci
?
BN + Ф
г
0)
.
Решив систему (11), найдем искомые
Z
?
, Фх0
и, соответственно,
гр1А
,
^Р1В
,
^Р1С
. Далее с учетом (1) станут известны комплексы:
и
1?
—
U1
?
ei
^
if
(
f— А,В,С
).
Рис. 3. Графическая интерпретация уравнений (10) и (11)
Затем определим комплексы токов первых абонентов следующим образом:
̇
= , где , – известные параметры, которые измеряются СЭА. Да
лее на
йдем токи: ̂
̇
= ̂
̇
-
̇
; ̇ = ̂
̇
+ ̂
̇
( = , , ) и продолжим расчет аналогично описанному для нулевого контура.
Практическая часть Рассмотрим трехфазную электрическую цепь (рис. 4). Модули действующих значений питающих напряжений фаз зададим так: = = = = = 220 В. Комплексные сопротивления фазных и нулевых проводников межабонентских участков одинаковы = на всех участках каждой из фаз и заданы в следующем виде: = = = (0,0012 + 0,000192) Ом ( =0, -1), что соответствует трем метрам кабеля АПВ сечением 70 мм2 [25]. Индуктивное сопротивление одножильного кабеля 5АПВ 1x70 определялось на частоте 50 Гц согласно [26] с учетом расположения его жил в одной плоскости на расстоянии двух диаметров.
Для расчетов использованы исходные данные нагрузок сети (табл. 1). Расчет цепи проводился в Mathcad методом узловых напряжений. Результаты расчета представлены в табл. 2. Следует отметить, что фазовые углы в табл. 2 записаны с учетом выражений (1). Результ
аты рас
чета коэффициентов , ( = 1,3, = , , ) согласно методике [3] представлены в табл. 3.
Таким образом, сделанные в теоретической части представленной работы выводы, касающиеся неработоспособности методики [3], подтверждаются результатами практических расчетов. На основе результатов табл. 2, которые брались в качестве исходных данных, был выполнен символьный расчет [27] уравнений (11) в Mathcad. Получены следующие результаты: модуль – = 0,001215 Ом; аргумент – = = 9,0902769 эл. град. Рис. 4. Трехфазная электрическая цепь с тремя ( = ) ответвлениями абонентов сети на фазу Таблица 1 Исходные данные
Абоненты фаз сети
Модули и начальные фазы сопротивлений нагрузки абонентов
№ абонента
Фаза сети
∗, А
, Ом
, эл. град
соѕ ( )
1
Л
40
5,5
45,0000000
0,707
в
2
110,0
11,4783400
0,980
с
10
22,0
66,4218215
0,400
2
А
20
11,0
11,4783400
0,980
В
20
11,0
45,0000000
0,707
С
4
55,0
66,4218215
0,400
3
А
10
22,0
11,4783400
0,980
В
5
44,0
66,4218215
0,400
С
22
10,0
66,4218215
0,400
Таблица 2 Результаты расчетов режима работы трехфазной электрической цепи
Абоненты фаз сети
Модули и фазы расчетных значений токов и напряжений абонентов
№ абонента
Фаза сети
и
, В
^, эл. град
I
, А
а
, эл. град
1
л
219,858025
0,0086987
39,974186
–44,9913013
в
220,004804
–0,0103061
2,000044
–11,4886470
с
220,012421
0,0240840
10,000565
–66,3977375
2
А
219,799021
0,0048309
19,981729
–11,4735100
В
220,007315
–0,0082293
20,000665
–45,0082293
С
219,992511
0,0382397
3,999864
–66,3835818
3
А
219,76858
–0,0010251
9,989481
–11,4793660
В
220,033083
–0,8034686
5,000752
293,5701438
С
219,967363
0,0512243
21,996736
–66,3705972
Таблица 3 Результаты расчетов коэффициентов Qи /
Абоненты фаз сети
Модули расчетных переменных по методике [3] для абонентов сети
№ абонента
Фаза сети
1
= ⁄
I
∗
V
= ⁄
и
∗
АВ
q
/
1
А
0,999355
0,999355
0,764873
0
0
В
1,000022
1,000022
0,200004
0
0
С
1,000056
1,000056
1,095507
0
0
2
А
0,999086
0,999086
0,199817
0
0
В
1,000033
1,000033
0,765392
0
0
С
0,999966
0,999966
1,095408
0
0
3
А
0,998948
0,998948
0,199790
0
0
В
1,000150
1,000150
1,095610
0
0
С
0,999852
0,999852
1,095283
0
0
Таким образом, предлагаемый в настоящей работе метод, представляющий собой систему уравнений (11), имеет аналитическое решение и дает значения сопротивлений межабонентских участков РЭС, соответствующие фактическим. Заключение Рассмотрена проблема определения векторов токов и напряжений в трехфазной распределительной сети напряжением 0,4 кВ при неизвестных сопротивлениях межабонентских участков РЭС на основе выполняемых АИИС КУЭ одновременных измерений за один и тот же интервал наблюдения действующих значений токов и напряжений, а также активной и реактивной мощностей в начале распределительной сети и у каждого ее абонента. Представлено теоретическое обоснование и практический расчет, указывающий на неработоспособность предложенного ранее [3] метода идентификации недоступных для измерения и контроля токов и напряжений, определяющих электрическое состояние межабонентских участков магистральной линии в режиме реального времени. Предложен новый метод вычисления векторов тока и напряжения в распределительной сети при условии, что сопротивления межабонентских участков РЭС неизвестны, а сопротивления фазных и нулевого проводов в пределах одного межабонентского участка являются одинаковыми. Полученные результаты помогут в дальнейшем развитии подсистем мониторинга электрического состояния в составе АИИС КУЭ.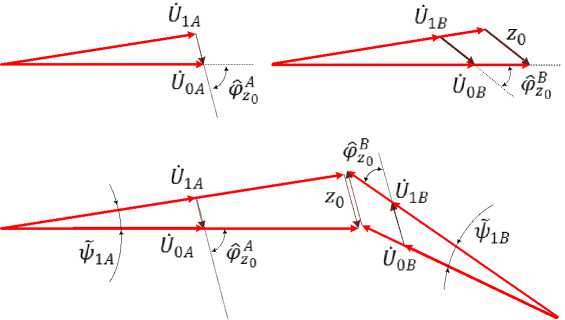
Список литературы К проблеме определения векторов тока и напряжения в распределительной сети по данным АИИС КУЭ
- Оморов, Т.Т. Идентификация и мониторинг потерь электроэнергии в распределительной сети в составе АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев // Электричество. - 2016. - № 11. - С. 4-11.
- Оморов, Т.Т. Определение параметров распределительных сетей 0,4 кВ по данным АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев, Р.Ч. Осмонова // Энергетик. - 2017. - № 6. - C. 37-40.
- Оморов, Т.Т. К проблеме моделирования несимметричных распределительных электрических сетей в составе АСКУЭ / Т.Т. Оморов, Б.К. Такырбашев, Р.Ч. Осмонова // Вестник ЮУрГУ. Серия "Энергетика". - 2017. - Т. 17, № 1. - С. 21-28. DOI: 10.14529/power170103
- Оморов, Т.Т. Параметрическая идентификация распределительной сети в составе АСКУЭ / Т.Т. Оморов, Р.Ч. Осмонова, Т.Ж. Койбагаров // Вестник ЮУрГУ. Серия "Энергетика". - 2018. - Т. 18, № 1. - С. 46-52. DOI: 10.14529/power180106
- Power System Reliability Importance Measures / M. Čepin, M. Demin, M. Danilov et al. // 29th European Safety and Reliability Conference, Hannover. - 2019. - P. 1633-1637. 10.3850/978-981-11-2724-3 0156-cd. DOI: 10.3850/978-981-11-2724-30156-cd
- Rejc, Ž.B. Estimating theadditional operating reserve in power systems with installed renewable energy sources / Ž.B. Rejc, M. Čepin // International Journal of Electrical Power & Energy Systems. - 2014. - Vol. 62. - P. 654-664.
- DOI: 10.1016/j.ijepes.2014.05.019
- Transmission line identification using PMUs / E. Janeček, P. Hering, P. Janeček, A. Popelka // 10th International Conference on Environment and Electrical Engineering, Rome. - 2011. - P. 1-4.
- DOI: 10.1109/EEEIC.2011.5874682
- Wu, Z. Simultaneous transmission line parameter and PMU measurement calibration / Z. Wu, L.T. Zora, A.G. Phadke // IEEE Power & Energy Society General Meeting, Denver. - 2015. - P. 1-5.
- DOI: 10.1109/PESGM.2015.7286115
- Zelenskii, E.G. Identification of the parameters of distribution networks by synchronized current and voltage measurements / E.G. Zelenskii, Y.G. Kononov, I.I. Levchenko // Russian Electrical Engineering. - 2016. - Vol. 87, no. 7. - P. 363-368.
- DOI: 10.3103/S1068371216070129
- Кононов, Ю.Г. Уточнение параметров участков линий сети среднего напряжения по данным синхронных измерений / Ю.Г. Кононов, О.С. Рыбасова, В.С. Михайленко // Известия высших учебных заведений. Электромеханика. - 2018. - Т. 61, № 1. - С. 77-84.
- DOI: 10.17213/0136-3360-2018-1-77-84
- IEEE Standard for Synchrophasor Measurements for Power Systems, [IEEE Std C37.118.1-2011 (Revision of IEEE Std C37.118-2005)], Dec. 28, 2011.
- Baumgartner, В. [The Impact of GPS Vulnerabilities on the Electric Power Grid / В. Baumgartner, С. Riesch, W. Schenk // XX IMEKO World Symposium, Benevento, Italy. - 2014. - P. 183-188.
- Load Monitoring Using Distributed Voltage Sensors and Current Estimation Algorithms / A.P. Grilo, P. Gao, W. Xu, M.C. de Almeida // IEEE Trans. Smart Grid. - 2014. - Vol. 5, no. 4. - P. 1920-1928.
- DOI: 10.1109/tsg.2014.2304011
- Пат. 2619134 Российская Федерация. Способ синхронизации измерений в электрических сетях по частоте и фазе напряжения силовой сети / Ю.Г. Кононов, П.А. Звада. - 2015.
- Solutions for detection of non-technical losses in the electricity grid: A review / L.V. Joaquim, R.E. Paulo, R. Melício et al. // Renewable and Sustainable Energy Reviews. - 2017. - Vol. 80. - P. 1256-1268.
- DOI: 10.1016/j.rser.2017.05.193
- Review of various modeling techniques for the detection of electricity theft in smart grid environment / A. Tanveer, C. Huanxin, W. Jiangyu, G. Yabin // Renewable and Sustainable Energy Reviews. - 2018. - Vol. 82. - P. 2916-2933.
- DOI: 10.1016/j.rser.2017.10.040
- Detection of energy theft and defective smart meters in smart grids using linear regression / S.-C. Yip, K.Sh. Wong, W.-P. Hew et al. // International Journal of Electrical Power & Energy Systems. - 2017. - Vol. 91. - P. 230-240.
- DOI: 10.1016/j.ijepes.2017.04.005
- Tanveer, A. Non-technical loss analysis and prevention using smart meters / A. Tanveer // Renewable and Sustainable Energy Reviews. - 2017. - Vol. 72. - P. 573-589.
- DOI: 10.1016/j.rser.2017.01.100
- Minimizing non-technical losses with point-to-point measurement of voltage drop between "SMART" meters / I. Bula, V. Hoxha, M. Shala, E. Hajrizi // IFAC-PapersOnLine. - 2016. - Vol. 49, iss. 29. - P. 206-211.
- DOI: 10.1016/j.ifacol.2016.11.103
- Сапронов, А.А. Оперативное выявление неконтролируемого потребления электроэнергии в электрических сетях напряжением до 1 кВ / А.А. Сапронов, С.Л. Кужеков, В.Г. Тынянский // Изв. вузов. Электромеханика. - 2004. - № 1. - C. 55-58.
- Patent no. 106405276 CN. Low voltage network electricity theft detection method based on AMI data / L. Wenpeng, Zh. Lei, Y. Yixin et al. - 2016.
- Пат. 2651610 Российская Федерация. Способ выявления мест возникновения и величин нетехнических потерь энергии в электрических сетях по данным синхронных измерений / Ю.Г. Кононов, Е.Г. Зеленский, М.В. Жуков, Р.Н. Липский. - 2016.
- Пат. 2700869 Российская Федерация. Способ определения мест неконтролируемого потребления электроэнергии в электрической сети 0,4 кВ / М.И. Данилов, И.Г. Романенко, С.С. Ястребов. - 2019.
- Данилов, М.И. Метод выявления мест неконтролируемого потребления электроэнергии в электрических сетях 0,4 кВ / М.И. Данилов, И.Г. Романенко // Изв. вузов. Электромеханика. - 2019. -Т. 62. - № 4. - C. 90-96.
- Провода установочные. - http:// kabelmag2012.narod.ru/Kab_ustanovS.html (дата обращения: 19.10.2019).
- Каменский, М. Силовые кабели 1-10 кВ с пластмассовой изоляцией. Расчет активного и индуктивного сопротивлений / М. Каменский, С. Холодный // Новости Электротехники. - 2005. - № 4 (34). - http://www.news.elteh.ru/arh/2005/ 34/15.php (дата обращения: 19.10.2019).
- Гурский, Д.А. Вычисления в Mathcad 12 / Д.А. Гурский, Е.С. Турбина. - СПб.: Питер, 2006. - 544 с.


