К проблеме повышения точности вычислительных схем в задаче аналитического продолжения гравитационного поля
Автор: Арсанукаев З.З., Рудаковская Е.Г.
Журнал: Вестник Пермского университета. Геология @geology-vestnik-psu
Рубрика: Геофизика
Статья в выпуске: 1 т.23, 2024 года.
Бесплатный доступ
Рассматриваются различные методы построения вычислительных схем разностного метода с использованием метода сеток при решении задачи аналитического продолжения заданных значений гравитационного поля на поверхности Земли в нижнее полупространство. Оценивается погрешность замены непрерывного уравнения Лапласа разностным уравнением. Приводятся результаты вычислительных экспериментов аналитического продолжения заданных значений поля при различных шагах сетки.
Разностный метод, уравнение лапласа, разложение в ряд тейлора
Короткий адрес: https://sciup.org/147245118
IDR: 147245118 | УДК: 550.83 | DOI: 10.17072/psu.geol.23.1.57
Текст научной статьи К проблеме повышения точности вычислительных схем в задаче аналитического продолжения гравитационного поля
Важнейшей проблемой в гравиметрии является решение обратной задачи. Традиционно обратная задача в гравиметрии решается методом подбора, суть которого в том, что в принятом модельном классе источников поля последовательно генерируются конкретные представители (конкретные распределения источников поля, принадлежащие модельному классу) и для них находятся (для точек, в которых выполнены экспериментальные исследования) соответствующие значения гравитационного поля от заданных представителей. Иначе говоря, для каждого представителя из принятого модельного класса источников поля решается соответствующая прямая задача, и далее вычисленные значения сравниваются (в выбранной метрике – обычно среднеквадратической) с полученными из наблюдений. Если по совокупности принятых критериев для некоторого представителя согласие наблюденных и вычисленных величин является приемлемым, то принимается, что данный представитель и определяет (вместе с другими фактами) интерпретацию аномального гравитационного поля в рамках принятой интерпре-
тационной модели. Но использование метода подбора на практике встречается с трудностями, иногда непреодолимыми, в связи с необходимостью использовать модельные классы источников поля большой сложности, включающие многие десятки и сотни тел, с достаточно сложными законами распределения плотностей в телах (линейные, квадратичные, экспоненциальные, логарифмические и другие законы изменения плотностей в телах). Это в свою очередь приводит к тому, что аналитические решения прямых задач, выражаемые определенными объемными интегралами, не всегда могут быть получены в явной форме. Что касается численных методов, то число конкретных прямых задач весьма велико; в то же время отсутствует комплекс компьютерных программ, реализующий все варианты решения прямых задач.
Другой подход, который разрабатывается авторами, заключается в аналитическом продолжении измеренных на поверхности Земли значений гравитационного поля в нижнее полупространство с использованием уравнений Лапласа и Пуассона. Уравнения Лапласа и Пуассона редуцируются разностными соотношениями к системе линейных диффе- ренциальных уравнений. В результате аналитического продолжения по поведению расчетного поля, получаемого в нижнем полупространстве, можно решать обратную задачу, т.е. определить контур области, занятую гравитирующими массами и плотности масс.
Метод сеток для дифференциальных уравнений
Обратимся теперь к основным положениям разностного метода и используемым аппроксимационным схемам (Крылов, Бобков и др., 1975). Рассмотрим несколько методов замены дифференциальных уравнений разностными уравнениями.
В основе первого метода лежит замена производных от функции и(х, у) разностными отношениями.
Пусть в некоторой области D, ограниченной контуром Г, задано уравнение
L(u) = а(х,у)ихх +
2 Ь(х,у')иху+с(х,у)иуу + 2 d(x,y)ux + 2 е(х,у)и у ++д(х,у)и = f(x,y). ( 1 )
Будем считать, что это уравнение в области D имеет эллиптический тип, т.е. для него выполняется условие 8 (х,у) = b2 (х,у) — а(х,у)с(х,у) < 0 всюду в D. Будем считать также, что к уравнению (1) присоединены граничные условия. Начнем с изложения понятия сетки.
Задача нахождения решения уравнения (1) в области D часто оказывается трудно разрешимой или вообще неразрешимой в конечном виде. Поэтому в практике вычислений отказываются от нахождения решения во всей области D и ставят задачу приближенно найти решение лишь на некотором множестве точек из D. Это множество точек называют сеткой. Его берут конечным и настолько густым, чтобы оно приближенно заменяло область D. При этом расположение точек сетки в принципе может быть любым. Обозначим через Dh множество точек сетки. Пусть [х1,у/) есть некоторая точка из Dh, а и(х[,у]) - значение функции и(х,у) в этой точке. Таких значений конечное число. Зада- ча их нахождения принципиально возможна. Она определяется дифференциальным уравнением, граничными условиями, присоединенными к этому уравнению, областью D и контуром Г. Суть метода сеток состоит в том, что на основе этой информации строятся некоторые соотношения, отражающие свойства дифференциального уравнения и граничного условия и позволяющие приближенно вычислить значения и(х1,х^).
Существуют несколько примеров выбора сетки. Остановимся на выборе прямоугольной сетки.
Проведем на плоскости переменных x и y совокупность прямых х = х 0 + ih ,у = у0 + jl, где хо, у о — координаты точки М, лежащей внутри D; h – шаг сетки по направлению x; l – шаг сетки по направлению y (h, l – положительные числа), i, j = 0,± 1 ,±2,±3 ... Точки пересечения этих прямых (х = х^, у = yj ), содержащиеся внутри области D, и образуют множество Dh точек прямоугольной сетки. Эти точки принято называть узлами сетки.
Пусть в области D задано дифференциальное уравнение (1). Рассмотрим прямоугольную сетку D h , заменяющую область D, и в ней точку (x i ,y j ) будем называть внутренней, если четыре её соседние точки (х 1-1 , у ] ), ( х ;+ 1 , у ] ), (хй у ]-1 ), (х 1 , у ]+1 ) при надлежат замкнутой области D = D+Г. Поставим задачу заменить дифференциальное уравнение (1) в точке (х^у ] ) сеточным уравнением. Такую замену мы выполним путем выражения каждой производной, входящей в уравнение, через значение функции в узлах сетки. Для функции и(х,у) двух независимых аргументов x и y соответствующие выражения имеют следующий вид
(du. _u(xi+1,yj)-u(xi - 1,yj)
(dx^yj) = h2 d3u
— Q dx3 \х+-е hyj)-1 < d <1 (2)
(du\ _ u(x i ,y j+i )~u(x i’ y j-i )
(dy)(xi,yj) = 21—
I 2 d 3 u
— (Tdy-y-^xtyj+T I) -1 < т <1(3)
д2и
(дТ)^ ) —
и(х +1, У ] )-2u(X i ,y j )+и(Х -1 У] ) h2
- 12 (~dXX^~)(X i +T ' h,y j ) > Кт <1 (4)
отсутствует смешанная производная, т.е. b(x, y) = 0 . Обозначим
a(x i ,y j ) = a tj ...’f(xbyj) = f ij .
Используя формулы (2)–(5) и уравнение (1), получим
(д2ич _
( ду2
u(X i ,y j+1 )-2u(X i ,y j )+u(X i ,y j-1 )
(Wi)I
1 2 д 4 u ч
-12 ( dy4 Xxiyj+al') 1<° <1
г i — д2 u
[L(u)] X i y j ) = a ij ( dx 2 ^У)
+C ij ( dy 2 )(Xiy ij ) + 2d ij ( dX ) (X i ’y j )+
+2 e ij t dy^X i y j ) + 9 ij u(x i ’y j' ) —
a ij
U(X +i yj}-2UXy}+U(X - i^^
c ij
2 ℎ
Uy j ^ + ib-lUy i ^b+Uy j ^-^
+
,d2u ч — Г д ддиу 1 _ dXdy (Xxyyi} [yy dXx J Xi’yj)
+2d ij
l2
u(X i+1 ’yj)-u(X i-1 y j )
2ℎ
+
+
^u\ ^u>.
( dx ) (xi’yj+i) ( dx ) (xi,yj-i)
+ 0(l2) =
2e ij
UXy+i}-UX i y j-i )
■++g ij U(xby j ) +
O( h 2 +l2) — f ij .
1 r U(X i+i ’y j+i ))+U(X i-i ,y j+i )
2l [ 2h
U(X i+i ,y j-i ))-U(X i-i y j-i )
Th
+0(l2)
+ 0(h2) -
0(h2)
в предположении, что ℎ=const. Отметим, что _ _ _ _ ~- д 2u для замены смешанной производной dXdy по формуле (6) используются точки в 4 углах большого квадрата и отмеченные на рис. 4 черными кружочками (формулы (2)–(5) получены из разложения функции u(Xi’Уj)в окрестности точки (x^yj) по формуле Тейлора с остаточным членом в форме Лагранжа.
Следует сказать, что приведенные здесь выражения для замены частных производных не являются единственными. Привлекая дополнительно значения u в других узлах сетки, можно получить ряд других замен, которые могут быть точнее вышеприведенных.
Перейдем теперь непосредственно к решению задачи: заменить дифференциальное уравнение (1) в точке (xi,yj) сеточным уравнением. Положим в этом уравнении (x,y)=(x j , y j ) и в целях упрощения будем считать, что в дифференциальном уравнении
Собрав в этом выражении члены при одинаковых сеточных значениях функции, будем иметь формулу
[ L(u)] (X i ’y j ) = L h (u(x i ’ y j )) +
+o( h2+l 2 ) = fij’ где положено
L h (u(x i , y j )) — A ij u (i+1 j) + ^ ij u (i-1 j) +
+Diju(ij+1) + Eiju(ij-1) + ?iju(ij) Aij = aij I dij n — aij dij n — cij । eij
~ + T ,^ ij - ~ - T , D ij -~ + T,
-2-22C-2^
CiJ 12 l ’ ^j h2 l2 + h +9iJ ’ u^ij) и т.д. - точные значения функции u(x,y) в точке (xi,yj). Если решение уравнения (1) имеет в области D непрерывные производные до четвертого порядка включительно, то в формуле (7) величиной O(h2+l2) при достаточно малых h и l можно пренебречь. Тогда окончательное сеточное уравнение, заменяющее дифференциальное уравнение (7), может быть записано в виде:
L h (u ij) — f ij ’ (8)
где под U ij понимается приближенное значение функции u(x, y) в точке (Х i ,y j ). Переход к этим приближенным значениям вызван тем, что в формуле (7) отбрасывается член О( h2+12 ). Этот член имеет смысл погрешности , с которой сеточный оператор L h (ui j' ) заменяет дифференциальный оператор L(u) во внутренней точке сеточной области. Для замены дифференциального оператора сеточным в этом случае привлекается схема точек (рис. 1), получившая название «крест». Сеточное уравнение (8) имеет место для всех внутренних точек сеточной области.
Рассмотрим теперь случай, когда в уравнение (1) входит смешанная производная g^y и b(x, y), следовательно, не равняется тождественно нулю. Замену этой производной осуществим по формуле (6) таким же путем, как и ранее. Сеточное уравнение, заменяющее дифференциальное уравнение (1) в точке к (x^yy ), в этом случае будет таким
-
71 h (u ij) = f ij .
При записи сеточного уравнения (9) использовалась схема точек (рис. 4), получившая название «ящик». Уравнение (9) имеет место во всякой внутренней точке сеточной области, при этом точку (х^у j} будем называть в случае схемы «ящик» внутренней тогда, когда восемь окружающих ее точек принадлежат области D . Изложенный выше метод замены дифференциального уравнения сеточным прост и удобен, но он существенно использует то обстоятельство, что сетка прямоугольная и равномерная (в ней узлы по каждому из направлений взяты равноотстоящими). Если сетка такими свойствами не обладает, то указанный способ замены не может быть осуществлен .
Рассмотрим теперь второй метод, основанный на аппроксимации дифференциального оператора в целом. Будем по-прежнему рассматривать уравнение (1). Предположим, что уже построена некоторая сеточная область Dh. Узлы сетки будем считать расположенными произвольно (это может быть и неравномерная и не прямоугольная сетка). Пусть по некоторому правилу мы отнесли часть узлов к внутренним, а часть узлов к граничным. Возьмем какую-нибудь внутреннюю точку с координатами x0, у0 и обозначим ее через Мо . Наряду с точкой Мо рассмотрим некоторую совокупность других внутренних точек Mi, М2 .., MN. Всего точек будет N+1. Обозначим через u(i) точное значение функции u(x, у) в точке Mi. Будем решать, как и прежде, задачу о замене уравнения (1) некоторым сеточным уравнением. С этой целью рассмотрим разностный оператор
L h (u( 0 )) = £ %= о с оk u(k) (10)
и в нем неизвестные параметры с ок определим таким образом, чтобы значение дифференциального оператора L(u) в точке Мо и значение Lh(u(о)) совпадали бы возможно более точно. Предположим, что все точки М1, М2 ..., MN лежат в достаточно малой окрестности точки Мо. Тогда разности xk -хо и У к -У о (1— k-N) будут малыми числами и значение функции u(k) можно разложить по формуле Тейлора в окрестности точки Мо (хо.,уо) (до производной r-го порядка включительно и с форме Лагранжа). воспользуемся для упомянутого выше
остаточным членом в Этим разложением мы того, чтобы добиться совпадения. Подставив это разложение в формулу (10), получаем:
L h (u(°)) = 'E p+q=о A pq ( g x p g y q ) ( о ) + ^ k=о с оk R(K) , где через (^^) ( о ) обозначено значение производной ^ ^ в точке М о , а через R(k) - остаток разложения.
Явные значения для коэффициентов Apq слишком громоздкие, поэтому ограничимся только указанием на их смысл:
-
1) эти коэффициенты линейно зависят от величин с о к (k=0,1,...N);
-
2) они содержат множители вида (х к -х о ) Р (У к -У о ) q -
- Если считать, что Хк — хо и Ук — у о являются малыми величинами одного порядка малости, то из последнего свойства следует, что коэффициенты Apq являются величинами, порядок малости которых относительно
(хк — x 0 ) или (yk — у 0 ) есть p+q. Потребуем, чтобы равенство
^ p+q =0 ^q ( g x p g y q ) ( 0) [k(u)] ( 0)
имело место для любой функции u(x,y), имеющей в области D непрерывные произ- водные до порядка r включительно. Для это- го необходимо, чтобы совпали коэффициен- ты правой и левой частях при
1 1+__, ( dx P dy q ) ( 00
для всех p и q, удовлетворяющих неравенству 0 < p + q < г. Это дает такую систему уравнений для определения величин с 00 ,с 01 ,...,с 0N :
А 00 = Ф 0 ,у 0 ) (p + q = 0 )
А 10 = 2d(x 0 ,у 0 ), А 01 = 2 е(х 0 ,У 0 ) (p + q =
А 20 = а(х 0 ,у 0 ), А 11 = 2 ^(х 0 ,у 0 ) А 02 =
с(х 0 ,у 0 ) (p + q = 2 )
А 30 =, А 21 = А 12 = А 03 = 0 (p + q = 3 )
А г 0 А 1— 11 • • •
(p + q = г).
А 1 г-1 = А 0 г = 0
Система уравнений возникает потому, что, вообще говоря, для коэффициентов
А pq верно представление
А pq =E k=0 « pq^ 0 к, (11)
где a pq(k - известные величины. Для определения величин с 0 к получим, таким образом, 1 (г + 1 )(г + 2) уравнений. Эти уравнения линейны. Встает вопрос о разрешимости системы линейных алгебраических уравнений. Если число уравнений системы будет больше числа неизвестных, то система может быть несовместной. Будем поэтому считать, что выполняется неравенство
1
(г + 1 )(г + 2)
Рассмотрим случай, когда 1(г + 1 )(г + 2) = N + 1. Предположим, что система уравнений для определения величин с0к имеет ранг, равный N+1, и, следовательно, она однозначно разрешима. Пусть решением этой системы являются числа с 00 *,с 01 *,..с 0 n* Таким образом, можно утверждать, что равенство
[Ф)] (0) = X N= 0 с 0 к*и(^')
выполняется с погрешностью
R * = 2 N= 0 сО к* и(к)
Если мы хотим выполнить замену дифференциального оператора сеточным во всей сеточной области, то аналогичные вычисления мы должны проделать для каждой внутренней точки. При этом число точек, привлекаемых для замены дифференциального оператора сеточным, может быть различным. Оно не обязательно должно быть равным N. Его можно увеличить или уменьшать в зависимости от того, каким мы хотим видеть остаток R * .
Отличие изложенных выше здесь методов состоит в следующем. В первом методе каждая в отдельности производная, входящая в дифференциальное уравнение, заменяется значениями функции, как правило, на равномерной сетке. Во втором методе отдельно каждая производная не рассматривается, а весь дифференциальный оператор заменяется в некоторой точке значениями функции на произвольной сетке. Второй метод более общий, но он требует, вообще говоря, для каждой точки систему уравнений вида (12). В первом методе этого не требуется, и в смысле простоты вычислений он предпочтительнее, а для получения желаемой точности можно брать более мелкий шаг. Иногда при замене дифференциального уравнения пользуются разностным интегрированием, но этот подход здесь не будет рассматриваться.
Определение параметров шаблонов 1-й крест», «2-й крест» для дискретной
аппроксимации уравнения Лапласа
Применим приведенные выше сведения из теории разностного метода при замене непрерывного уравнения Лапласа (уравнение эллиптического типа), описывающем поле тяжести вне возмущающих масс, дискретным уравнением.
Пусть в некоторой области D, ограниченной контуром Г, задано уравнение Лапласа
-
л — д2и . д2и
-
-• ■. +тут = 0
и к нему присоединено граничное условие и| Г = у(М)(13)
Поставим задачу: заменить оператор Ди сеточным оператором. Будем рассматривать случай квадратной сетки, когда h = l. Координаты узла сетки будем определять по формулам хк = х 0 + к h, ук = уо + к к, к = 0, ± 1, .„
Заменим область D сеточной областью D h и в ней выделим D h * внутренних узлов и множество Г граничных узлов. Узел будем называть внутренним , если четыре его соседних узла принадлежат области D=D+r. Пусть узел с координатами (Х [ у) является внутренним. Для замены в этом узле дифференциального оператора сеточным изберем схему точек «крест» и в ней пронумеруем точки в таком порядке, как показано на рис. 1.
fij+1
1*ij-1
Рис. 1. Схема точек «крест»
Составим выражение для сеточного оператора L h (и(0 )) = £ к= о с ок и(к) (14) и в нем величины с о к определим так, чтобы равенство ((Ди) ( о) = L h (и(0 )) выполнялось с возможно большей точностью. Используя разложение в ряд Тейлора выражения (14) и сравнивая, как и выше, коэффициенты, стоящие в этом выражении при и(О), (^^ о ) ,
(^) (о) и т.д. с аналогичными коэффициентами в выражении (Ди) (о ) , получим систему линейных алгебраических уравнений для определения величин с о к :
-
с оо + с о1 +с о2 +с оз + с о4 =0,
-
(-с о1 + с оз ) h =°.
-
(-с о2 + с о4 ) ^ 0.
-
(с о1 + с оз ) ^=1.
-
(с о2 + с о4 ) ^=1.
ℎ3
-
(- с о1 + с оз ) ^=0,
ℎ3
-
(- с о2 + с о4 ) ^=0
Решение этой системы легко выписывается:
-
с о1 = с о2 = с оз = с о4 У2 , (15)
ℎ соо=- h2.
Таким образом, сеточный оператор, заменяющий дифференциальный оператор Д и в точке (Х [ у) на схеме точек «крест», будет иметь вид
L h (и( о )) = 1 2 (и(1)+и(2)+и(3)
+u(4)-4u(0)). (16)
Если функция и(х,у) имеет в области D непрерывные производные по x и y до четвертого порядка включительно, то имеет место формула (т.е. замена дифференциального оператора разностным отношением осуществляется с точностью до бесконечно малых второго порядка малости)
(Ди) (о ) = L h (и( о )) + O( h2 ).
Таким образом, замена дифференциального оператора (12) разностным оператором (14) приводит непрерывное уравнение Лапласа Ди = о , рассматриваемое в узле ((Х[.yj) к дискретному уравнению Lh (и(о)) = 1 2 (u(1)+u(2)+u(3)+u(4)-4u(0))=0; или после сокращения на р" ^ о к
u(1)+u(2)+u(3)+u(4)-4u(0)=0. (17).
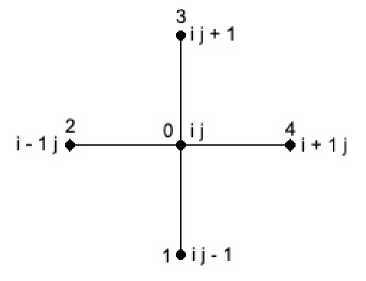
Рис. 2. Схема точек «1-й крест»
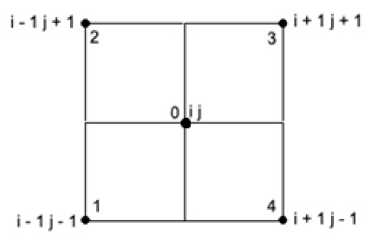
Рис. 3. Схема точек «2-й крест»
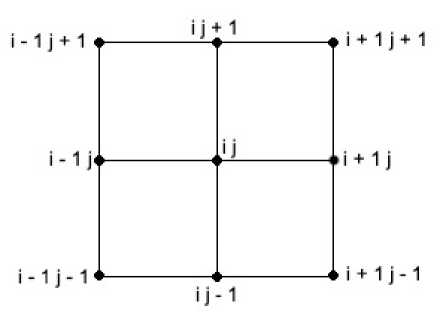
Рис. 4. Схема точек «ящик»
Рассматривая дискретное уравнение Лапласа (17) во всех внутренних узлах заданной сеточной области при схеме точек « крест» с присоединением граничных условий, придем к системе линейных дифференциальных уравнений:
Ax = f, (18) где A - матрица системы (18) - состоит из коэффициентов уравнения (17)
-
с 01 = с 02 = с 03 = с 04 = 1 , с 00 = - 4 ;
х - вектор неизвестных значений поля; f -вектор заданных значений поля (граничные условия). Следует отметить, что матрица A очень разреженная: в некоторых модельных примерах число ненулевых элементов в одной строке матрицы от 1 до 25, тогда как число нулей в этой же строке может быть до нескольких десятков тысяч.
Решение задачи аналитического продолжения гравитационного поля с использованием дискретного уравнения Лапаласа на модельном примере
Дискретное уравнение (17), редуцированное к системе линейных алгебраических уравнений (18), было использовано в задаче аналитического продолжения заданных значений поля на поверхности Земли в нижнее полупространство в следующих модельных условиях. В качестве аномалиеобразущего тела принимался объект простейшей формы, поскольку в этом случае соответствующий объемный интеграл, представляющий решение прямой задачи (решением является вертикальный градиент гравитационного потенциала т л ) вычисляется в конечном виде, т.е.
OZ решение прямой задачи является точным. Решения прямой задачи используются далее в качестве «входных» значений в задаче аналитического продолжения в модельных условиях. Помимо этого, точные решения прямой задачи позволяют оценивать точность расчетных значений в нижнем полупространстве, полученных в результате аналитического продолжения, путем сравнения в соответствующих узлах с точными решениями прямой задачи. Одним из таких тел является прямоугольный параллелепипед бесконечного простирания в направлении одного из своих измерений (в данном примере в направлении оси Oy, т.е. перпендикулярно плоскости рисунка) и имеющего сечение 2.0х 2.4 км). Таким образом, решается двумерная задача, избыточная плотность тела принимается равной 1 г/см 2. Заданные значения поля (решения прямой задачи) располагаются на двух уровнях (профилях): на уровне Земли z = 0 и на уровне шага сетки y над уровнем Земли z = -h; (ось Oz направлена вниз). Длина каждого профиля 16 км, шаг сетки равен 0.4 км, сеточная область представляет собой прямоугольник с основанием, равным длине профиля (16 км) и высотой, равной расстоянию от z = 0 до верхней кромки параллелепипеда, находящейся в нижнем полупространстве на глубине 4 км.
Отметим сразу, что задача является некорректной (в классической постановке это задача о решения уравнения Лапласа в прямоугольнике (сеточной области) – так называемая задача Дирихле, где заданы граничные условия по всему контуру прямоугольника), поскольку почти всегда измеренные значения поля находятся на верхней стороне прямоугольника на уровне z = 0 или выше, иногда на боковых сторонах прямоугольника (при наличии данных шахтной гравиразведки) и никогда на нижнем основании прямоугольника.
Матрица системы (18) в условиях данного модельного примера имеет размерность 390 х 410, т.е. число уравнений равно числу внутренних узлов: 39 узлов на одном профиле умножено на число уровней, равное 10, всего 390; а число неизвестных значений поля равно числу неизвестных значений поля на одном уровне, умноженному на число уровней, т.е. 41 х 10 = 410 . Решение системы (18) проводилось методом итерации (Страхов В.Н., Страхов А.В., 1999), и оно оказалось неустойчивым, что объяснимо, когда система является недоопределенной , т.е. число уравнений меньше числа неизвестных. В нижнем полупространстве только на отметке, равной одному шагу сетки от поверхности Земли, (z = 0) относительная погрешность (в среднеквадратичной норме) расчетных значений была порядка 10 - 1 (т.е. разница в расчетных значениях поля и точных решений прямой задачи составила около 10 %), а ниже этой отметки относительная погрешность была уже более 100 %, т.е. начался распад поля. Было решено обеспечить устойчивость решения системы (18), рассматривая совместно две дискретные аппроксимации уравнения Лапласа: к схеме точек «крест» (которая дальше будет называться «1-й крест» (рис. 2)) добавляется схема точек «2-й крест» (рис. 3). Для решения предыдущей задачи о замене дифференциального оператора J u в точке (% j ,у;-) изберем иную схему точек (рис. 3). В этом случае оператор имеет вид
Lh'(u( 0 )) = ^ (u( 1 ) + u( 2)+
+u( 3 ) + и( 4) — 4 u( 0)).
Соответствующие этому вычисления мы опускаем, они аналогичны предыдущим. Имеет место также формула
(Ли) (0 ) = Lh ’ (u( 0 )) + O( h2 ).
Операторы L h (u( 0 )) и L h* (u(0 )) одинаковы по виду, однако качество их различно, так как различными являются схемы точек, на которых эти операторы заменяют дифференциальный оператор J u.
Как и в случае схемы точек «1-й крест», записывая дискретное уравнение Лапласа для схемы точек «2-ый крест»
Lh *(«( 0 )) = 12( (u( 1 ) + u( 2 )+
u( 3 ) + u( 4 ) — 4 u( 0 )) = 0 , после сокращения на ^ Ф 0 получим вторую дискретную аппроксимацию уравнения Лапласа
u( 1) + u(2) + u(3) + u(4) — 4u(0)=0 (19), где C 01 = C 02 = C 03 = C 04=1, C 00=—4
являются элементами матрицы A вместе с коэффициентами первой дискретной аппроксимации уравнения Лапласа.
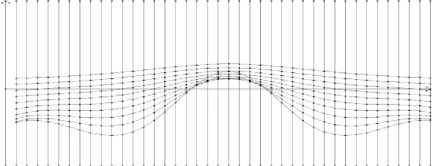
Полученная система (18) теперь будет переопределенной (т.е. число уравнений будет больше числа неизвестных) с матрицей, имеющей размерность 780х 410. Решение ее является уже устойчивым – результаты расчетов, представленные с помощью специальной программы в графической форме (Арсанукаев З.З., Арсанукаев И.З., 2015), приведены на рис. 5 а (на оси ординат расположены значения -- поля в мГал, на оси абс-dz , цисс – координаты узлов сетки на профиле). Чтобы увеличить точность вычисляемых значений поля, расчеты проводились и на более густых вариантах сетки, т.е. с меньшими шагами сетки (рис. 5 б, в). Отметим, что на рис. 5 а, б, в самая верхняя кривая построена для расчетных значений поля в узлах уровня, расположенного на расстоянии шага сетки от поверхности Земли (z = h) в нижнем полупространстве, а самая нижняя кривая построена для расчетных значений поля в узлах уровня, расположенного на уровне верхней кромки аномалиеобразующего тела.
двум дискретным аппроксимациям «1-й крест» и «2-й крест» девятиточечной схемы «ящик» (рис. 4). Имеет место следующая формула:
(Ли)т = 1 [4Lh(и(( Xi,yj)) +
L h * (и(( x i , y j ) ) ]- 2 ^ (J 2 u) (ij) - 7 [ J 3 и + 2 d 4 . , ,
^—; Au] ( Х + с h,y j +T h ) , ГДе -1< с , т <1 (Канторович, Крылов, 1962).
Рис. 5 а. Аномальные кривые при шаге сетки 400 м (10 кривых)
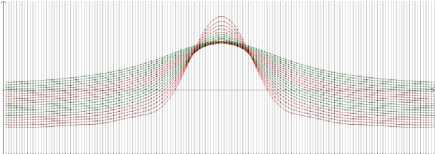
Рис. 5 б. Аномальные кривые при шаге сетки 200 м (20 кривых)
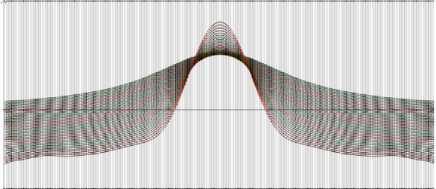
Рис. 5 в. Аномальные кривые при шаге сетки 100 м (40 кривых)
Анализ результатов расчета показывает, что на глубине, равной шагу сетки от уровня z = 0, относительная погрешность на шагах сетки 400, 200,100 м имеет значения, порядок которых соответственно 10 - 3 , 10 - 5 , 10 - 6 (т.е. восстановленные значения отличаются от точных, например для шага 200 м в среднем на 1/1000 %), а на глубине, расположенной выше отметки верхней кромки тела на 1 шаг сетки, погрешность имеет порядок 10 - 1 , 10 - 2 , 10 - 3 (т.е. для шага 200 м восстановленные значения отличаются от точных в среднем на несколько процентов).
Следующим шагом в повышении точности стоящих в узлах схемы значений поля, получаемых в результате аналитического продолжения, является присоединение к
Аналогично предыдущему, с точностью до бесконечно малых 2-го порядка, получим для схемы «ящик» на равномерной сетке дискретное уравнения Лапласа:
4Lh(u((xi,yj)) + Lh* (и((Хру7))=0, или
4(и( 1) (1 )+и( 1) ( 2 )+и( 1) ( 3 )+и( 1) ( 4 )-4u(0))+ (u( 2) (1 )+u( 2) ( 2 )+u( 2) ( 3 )+u( 2) ( 4 )-4u(0)=0, или
0,8(u( 1) (1 )+u( 1) (2 )+u( 1) ( 3 )+u( 1) ( 4 ))+0.2( u( 2)(1 )+u( 2)( 2 )+u( 2)( 3 )+u( 2)( 4 )) -4u(0) = 0, где u( 1)(1), u( 1)(2 ),u( 1)( 3 ),u( 1) ( 4) - значения поля, стоящие в узлах схемы «1-й крест» внутри схемы «ящик» (кроме узла 0, рис. 4); u( 2)(1 ),u( 2)( 2 ),u( 2)( 3 ),u( 2)( 4 ) - значения поля, стоящие в узлах схемы «2-й крест» внутри схемы «ящик» (кроме узла 0, рис. 4); u(0) – значения поля, стоящие в центре схемы «ящик» (рис. 4). Коэффициенты схемы «ящик»
-
( 1 ) ( 1 ) ( 1 ) ( 1 )
c 01 = c 02 = c 03 = c 01 = 0.8,
-
( 2 ) ( 2 ) ( 2 ) ( 2 )
c 01 = c 02 = c 03 = c 01 = 0.2, c 00=-4, служат далее элементами матрицы, а вместе с коэффициентами двух дискретных аппроксимаций «1-й крест» и «2-й крест» уравнения Лапласа. Матрица A системы линейных алгебраических уравнений, полученной в результате использования совместно трех дискретных аппроксимаций уравнения Лапласа:
«1-й крест», «2-й крест» и «ящик», будет переопределенной, и ее размерность для данного модельного примера равна 1170 х 410 . Как можно видеть из табл., точность расчетных значений поля для уровня, расположенного на 1 шаге сетки в нижнем полупространстве от уровня Земли (z = 0), увеличивается на порядок по сравнению с вычислительной схемой «1-й крест» + «2-й крест».
Дальнейшее выполнение аналитического продолжения измеренных значений поля на поверхности Земли с использованием уравнения Лапласа и метода сеток позволяет по изменениям в аномальных кривых определить положение верхней кромки гравитирующего тела, найти его центр тяжести, верхние особенности тела (при наличии) с помощью функции Березкина и в некоторых случаях положение нижней кромки.
Таблица
|
Глубина, км |
Относительная погрешность точ выч X - X Е точ X Е |
|
|
«1-й к» + «2й к» |
«1-й к» + «2-й к» + «ящ.» |
|
|
0,4 |
1,38440Е-03 |
4,92070Е-04 |
|
0,8 |
3,90422Е-03 |
3,492533Е-03 |
|
1,2 |
9,60364Е-03 |
4,769514Е-03 |
|
1,6 |
1,85948Е-02 |
1,069080Е-02 |
|
2,0 |
2,96881Е-02 |
2,459834Е-02 |
|
2,4 |
4,46757Е-02 |
4,197743Е-02 |
|
2,8 |
7,05478Е-02 |
6,123032Е-02 |
|
3,2 |
1,15451Е-01 |
8,713836Е-02 |
|
3,6 |
1,84324Е-01 |
1,312850 Е-01 |
По полученным расчетным значения поля в точках контура области, занятой тяготеющими массами, можно осуществить аналитическое продолжение внутрь области при помощи уравнения Пуассона с определением плотности масс и таким образом решить обратную задачу.
Заключение
В результате проведенных исследований с использованием различных вычислительных схем разностного метода определено, что при численном решения уравнения Лапласа на неполном контуре могут быть получены устойчивые решения соответствующих систем линейных алгебраических уравнений с построением по этим решением аномальных кривых. По изменениям в аномальных кривых можно затем решать задачу оконтуривания области, занятой тяготеющими массами.
Список литературы К проблеме повышения точности вычислительных схем в задаче аналитического продолжения гравитационного поля
- Арсанукаев З.З., Арсанукаев И.З. Программа аналитического продолжения заданных на поверхности Земли значений гравитационного поля в нижнее полупространство с использованием дискретных схем и решения систем линейных алгебраических уравнений больших порядков на модельных примерах. Свидетельство о государственной регистрации программ для ЭВМ (SOFT). #2015661026, 15 октября 2015 г.
- Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М., 1962. 531 с.
- Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы высшей математики. Т. 2. Минск: "Вышэйшая школа", 1975. 672 с.
- Страхов В.Н., Страхов А.В. Основные методы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии. II М.: ОИФЗ РАН, 1999. 51 с.


