К проблеме проводимости полимерных пленок на примере полибензимидазолов

В рамках плазменно-гидродинамической концепции состояния ионов в растворах электролитов нами было получено уравнение для расчета электрической проводимости электролитных систем [1,2]. Существенным аргументом в пользу полученного уравнения для теоретических оценок электрических проводимостей явилось установление концептуального единства теории электропроводности растворов электролитов с теорией проводимости твердых тел.

Решение данной проблемы было основано на применении четырехмерного уравнения движения зарядов в ковариантной форме при определении проводимости X в растворах электролитов:

dP     dU

-= = mcI---L I = I - IFikUk

dt        dS c ik или в развернутом виде:

mc I

при условии, что под дважды повторяющимися немыми индексами подразумевается суммирование. В

dx уравнениях (1) и (2) Ui- = —^ - четырехмерная скорость; dS = cdt 1

v

u

- -

2 ) 2

r 2

c 7

- пространственный интер-

вал, при u <<  c , dS = cdt ; P ^ = mcU i - импульс. Величина F_ik представляет собой антисимметрический ковариантный тензор электромагнитного поля, который можно представить в виде матрицы, где индекс i =0, 1, 2, 3 нумерует строки, а индекс k =0, 1, 2, 3- столбцы, при этом электрическое поле E_y направлено вдоль оси Y , а магнитное H_z - вдоль оси Z :

F i0 —

к

i	°	1	2	3
k
°	°	E x	Ey	E z
1	- E x	°	- H z	H y
2	- Е Ey	- H z	°	H x
3	- E z	Hy	H x	°

•

л

Анализ уравнения (2) возможен по двум направлениям:

• 1)    по временной координате i =°;

• 2)    по пространственной координате i =1, 2, 3.

Таким образом, при i =°, согласно матрице (3), магнитное поле отсутствует вообще, а скорость и у направлена вдоль поля Еу . При данных условиях решение уравнения (2) для истинных траекторий . г PdV      _ движения зарядов в системе с потенциалом ф — ----, где р - плотность зарядов, dV — 4nr dr - эле-

R мент объема, а R - расстояние от точки наблюдения до dV, имеет вид:

и —

— |(U - 2 вф)

. m 7

2Z

^J m •

При i =1, 2, 3 решение уравнения (2) при заданной геометрии сил: cE_yt

и — 7,

У   2m • (1 - itot)

eHz где У =--есть частота циклотронных колебаний. mc

Таким образом, найденные значения скоростей (4) и (5) для временной и пространственных компонент уравнения (2), при их последующем использовании в уравнении для расчета проводимости в растворах электролитов, приводят к равенствам:

_ ^FU у

^ v —

y

Ey

F

ЕЦ- к

— (U - 2вф) m

• f m ,

X     n ° ^{в и} у       n ° в ² 1

• ^у     Е у     2 m • ( I - i to t )

Следует отметить, что уравнение (7) при i to t — 1 обладает сверхпроводимостью [3].

Очевидно, что при H z — ° имеет место У — ° , и уравнение (7) трансформируется в классическую формулу Друде для проводимостей твердых тел в постоянном электрическом поле:

X _— n ° ^{в 2} t ^у 2 m

•

Таким образом, выражение (8) можно использовать при оценке проводимостей любых кристаллических структур, в том числе и квазикристаллических. Тем самым, нам представляется возможным применение данной модели для теоретической оценки протонной проводимости полибензимидазольных полимерных пленок, допированных ортофосфорной кислотой (ПБИ).

Рассмотрим элементарное звено макромолекулы ПБИ (рис.1).

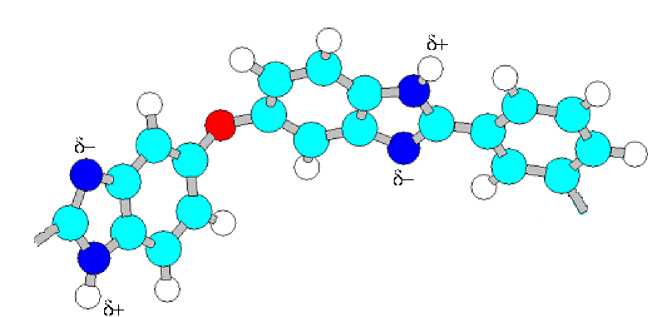
Рис. 1. Элементарное звено полибензимидазола

В элементарном звене расстояние вдоль макромолекулы между частично положительным и частично отрицательным зарядами на атомах водорода, согласно квантовомеханическому методу расчета

+     —

ММ+, равно l = 9,11 - 10 - ⁸ см. Данные заряды 5 и 5 представляют собой свободные вакансии, на которые ориентируются ионы, полученные в результате диссоциации ортофосфорной кислоты:

H 3 PO 4 □ H ⁺ + H 2 PO₄ ,       К д 6,31 - 10 - 3 .

Количество свободных вакансий в элементарном звене ПБИ можно определить исходя из экспериментальной плотности макромолекулы:

N _ ^Р ПБИ N _ -0,9- - 6,02 - 10²³ = 2,7 - 10²¹ .

^{вак . М} э ( эл . звена ) ^{A 198,5}

Концентрация ионов, полученных в результате диссоциации ортофосфорной кислоты, рассчитывается на основании закона разбавления Оствальда, при этом исходная концентрация составляет C o = 11 моль/л :

[ Н ⁺ \_[ HPO 4      К д - C о = 4 6,31 - 10 - ³ - 11 = 0,263 моль/л.

Тогда в 1 см ³ содержится ионов:

N _ 0,263 - 6,023 - 10²³

1,58 - 10²⁰ .

Следовательно, можно сделать вывод, что только при достаточном объеме допирующего раствора ортофосфорной кислоты все свободные вакансии будут заняты. И в этом случае протонная проводимость ПБИ будет минимальна.

Если число ионов H ⁺ и H ₂ PO - превысит число свободных вакансий, то возможен процесс:

H ₂ PO 4 + H ₂ PO ₄ □ HPO ₄ ^{2 -} + H ₃ PO ₄ .

+

В этом случае один ион H2PO- ориентируется в положение 5 , а второй ион H2PO- образуется при диссоциации избытка H3PO4 . Образующийся протон H+ является по существу свободным и мо- жет рассматриваться как носитель тока. Концентрация ионов также определяется из закона разбавления Оствальда. При этом учитывается константа диссоциации уже второй ступени:

[ Н ⁺\_ V К Д - с ₀ _ 6,3 - 10 - ⁸ - 0,26 _ 1,29 - 10 - ⁴ моль/л.

Тогда в 1 см ³ содержится ионов:

1,29 - 10 - ⁴ - 6,023 - 10²³

7,75 - 10¹⁶ .

n =—=------

0          1000

В формуле (8) t - есть время релаксации или, иначе, время свободного пробега носителя тока, оп- ределяемое выражением:

l t=—, uy

где u _y - тепловая скорость движения:

u y

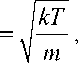
здесь m - масса иона H ⁺ . Тогда

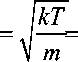
I 1,38 - 10 ^{- 16} • 298 = 1,66 • IO ^{- 24}

15,7 • IO⁴ см- .

сек

Находим время релаксации:

l    9,11 • 10 ^{- 8}

0,58 - 10 ^{- 12} сек .

t = — =^=— и    15,7-104

При подстановке полученных значений n ₀ и t в формулу Друде (8) получаем проводимость ПБИ в электростатической системе единиц:

. 7,75-1016 • 23-10-20 • 0,58-10-12    ..о-1

X = —=------------^ --------- 62 " 10 сек .

1,66 •Ю ^{- 24}

Иначе:

2 62•Ю8 ,,

X =---=-— 6,9 •Ю См / см .

• 9 • 10¹¹

Полученное экспериментально четырехзондовым методом Ван-дер Пау значение протонной проводимости ПБИ, допированных 11М раствором ортофосфорной кислоты, составляет X = 4,9 • 10 ^{- 3} См / см .

Таким образом, теоретически оцененная протонная проводимость полимера хорошо коррелирует с экспериментально полученным значением.