К радиальной теории ионного тока на зонд: I. Учет объемной ионизации

Радиальная теория ионного тока на зонд в плазме низкого давления впервые была предложена в работе [8] и развивалась в последующем в [9], [13], [15], [17]. Приближение радиального дрейфа наиболее применимо в том случае, когда ионная температура T_i близка к нулю (ионы обладают незначительным моментом количества движения) и выполняется приближение бесстолкновительного движения. При этом даже редкие столкновения ионов с атомами разрушают орбитальное движение частиц и сильно влияют на величину ионного тока [1], [7]. Вследствие этого радиальная теория дает лучший результат при наличии столкновений, чем более строгая орбитальная теория [11], [16].

В радиальной теории пренебрегается орбитальным моментом ионов (полагается T_i / T_e = 0, где T_e – температура электронов), которые движутся радиально со скоростями, определяемыми локальным потенциалом и законом сохранения энергии. В этом случае возможно численное решение уравнения Пуассона без разбиения на области квазинейтральной плазмы и слоя [8]. Ионный ток задается на бесконечности, а ионизацией в объеме пренебрегается. Концентрация электронов предполагается распределенной по больцмановскому закону n_e = n ₀ exp( e^- ) , где n 0 - kT_e концентрация невозмущенной плазмы. Тогда уравнение Пуассона для цилиндрического и сферического случаев соответственно запишется:

При заданном ионном токе I_з эти уравнения интегрировались численно [9], [13] при граничных условиях: r → ∞, n → n ₀ , φ → 0, d φ / dr → 0 для отношений радиуса зондов к электронному дебаевскому радиусу — >  0,25 - цилиндр и - ³ - >

A i ^л д

≥ 0,05 – сфера. В [15] рассчитывался плавающий потенциал сферического зонда в широком диапазоне 10 ^{- 4}< — <  10 ⁴ для аргона и гелия, но вольт-

Ад амперные характеристики не рассчитывались.

Отсутствие учета объемной ионизации в радиальной теории требует увеличения области возмущения до бесконечности, в противном случае вся плазма конечных размеров уйдет на зонд. Кроме влияния на ионный ток конечное значение области возмущения плазмы зондом определяет пространственное разрешение метода. Ионизация в объеме учитывается в работах по пристеночному потенциалу, когда стенка интерпретируется как большой зонд. В основополагающей работе Тонкса и Ленгмюра [18] получено уравнение «плазма-слой»:

V ² Ф = - - е о r “ «

о

r r ' “ n о exp⁽

^еф:1 ) dr -kT e

о

^ 2 e ( ф ( r ') - ф ( r ))/ M

е ф ( r ) ^- n о exP^y^) kT_e

^ , (3)

1 d , dp.

( r —) r dr dr

e e о

I з

2 n rl з e 7 - 2 с ф IM

, сф_х ^- n o ^exp⁽—) kT_e

1 d , ₂ dp.

—г — ( r —) = r ² dr dr

-

e e о

I,              ,фх

---:—, ³       г - n ₀ exp(——) 4 n r ² e j - 2 с ф IM        kT_e

здесь z – частота ионизации, производимой од-r'“ ним электроном, —zne (r^)dr- плотность пото-ra ка ионов в точке r, родившихся в элементе dr', где α = 0 – плоский случай, α = 1 – цилиндрический случай, α = 2 – сферический случай.

Численные расчеты выполнены для области квазинейтральной плазмы, где принималось n_i = n_e . Результаты [18] показали, что учет генерации ионов приводит к возрастанию потенциа-

ла и средней скорости ионов на границе плазмы и уменьшению ионного тока на слой. Это отклонение от случая отсутствия генерации при внешней стенке возрастает с переходом от плоской к цилиндрической и далее к сферической геометрии. Впоследствии результаты [18] уточнялись в [10], [12], [14].

В [6] рассмотрен учет объемной ионизации в радиальной теории при конечной области возмущения плазмы ''rQ". Применено уравнение «плазма-слой» Ленгмюра (3) для ионного тока, но с иными граничными условиями: на внешней границе r = r принималось ф = 0, — — 0. В работе dr определяли зависимости плавающего потенциала зонда (пылевой частицы в плазме) и связанного с ней значения r0 / Хд от частоты ионизации. Столкновения с атомами не учитывались.

В настоящей работе рассматривается ионный ток на сферический и цилиндрический зонды с учетом ионизации в приближении холодных ионов. Вычислены вольт-амперные характеристики для безразмерных параметров г з / Х д = 0,0001 ^ ^ 10, A = z / m i = 0,02 ^ 5, где m i - ионная плазменная частота.

ИСХОДНЫЕ УРАВНЕНИЯ И АЛГОРИТМЫ РАСЧЕТА

Пусть r - область возмущения плазмы. В [2], [4] область возмущения определяется объемом плазмы вокруг зонда, в котором при пренебрежении объемной рекомбинацией число образующихся в единицу времени ионов за счет ионизации равно току на зонд. Для холодных ионов в радиальной теории это определение соответствует нулевой дрейфовой скорости ионов на границе области возмущения. В единице объема за единицу времени образуется n z ионов. При этом все ионы, поступающие на зонд, создаются внутри rQ. Ионы, образовавшиеся вне r0, уходят на стенку и электроды. Этот уход и определяет частоту ионизации, производимую одним электроном, z ~ j^, где N- полное число электронов в объеме, jcm, Scm - плотность ионного тока на стенку и площадь стенки.

Рассмотрим формирование потока ионов на зонд внутри rQ. На элементе пути иона dr' образуется доля новой плотности тока:

dj = en e ( r ') zdr ' .                        (4)

Все ионы доли плотности тока (4) будут иметь скорость J— [ф(r') - ф(r)]. Разделив долю потока M на скорость, получим долю концентрации dn'. Полные концентрация и плотность тока в точке r будут равны

1 r 0

^{n ( r} ) = r a J r

r'° n e ( r ') zdr '

I e [ ф ^{( r} ') ^- ф ^{( r )]}

M

e ^r 0

, j ^{( r} ) ^— — [ n e ^{( r ) zr} dr . (5) r ^J

r

Введем безразмерные параметры:

r re                     п л     z^

x = ^г= / ™ , ; и — -e^; n' = —; a == —;

^д ^sо kTe I n о       kTe      n 0      \TTe IM ®i j' =    i,     , здесь го. - плазменная ионная час- en о kTe IM‘ тота, j - плотность тока, Хд - электронный дебаевский радиус.

Подставляя выражение (5) в уравнение Пуассона при больцмановском распределении концентрации электронов, получим в безраз- мерных величинах:

д ² U а д U

ТГ + — дx    x дx

a x ⁰

= exp( U ⁽ x )) — a j x_x

x ^a exp( U ( x ')) dx '

4 2[ U ( x ') - U ( x )] . ⁽⁶⁾

Решение (6) от границы области возмущения затруднено нулевыми начальными условиями для потенциала и его градиента. В [6] для начального от границы тонкого слоя, считающегося плоским, A x <<  x ₀ = x N получено приближенное аналитическое решение в предположении n ' = 1; n' = const :

eN

U ( x ) = (1 - n ' n ) ⁽ xN - x ⁾² ,                              (7)

,   1  , П   B   IB B2  , П   B IB  BB n + 31+           1+ 311

^N 3  \ 27  2  \ 27   4    227   2 227   4 ’

_ A П2

где B —    . Однако при распространении реше ний (7, 8) на достаточно толстый слой плазмы, особенно при больших xN, где x'N^ 1, возникают неустойчивости счета. Ввиду этого методом последовательных приближений решение (7) было уточнено:

U ( x ) — (1 - n\ ) ⁽ x N - x ⁾² (1 + у x ), (9)

2           xN где y —

1 , 363 n 'N - 1

1 , 818 n N - 1 , 5

.              1,363 n_N - 1

- для сферы и Y =     ,—7

3,636 n _N - 3

для цилиндра.

1 + A [1 - (2 + z ) ] x_N П

ⁿ ' n - 1 = ⁿ ' n

где h - шаг дискретизации координаты. Эти зна- чения потенциала и концентрации принимались в первой от границы точке xN- 1. Для нахождения потенциала в следующих промежуточных точках использовалась трехточечная параболическая интерполяция для значений U(x):

x - x, .      x - x,

2UX — 2U,- + a,(------j )2 + b,-------j, x j jV h           j h ’ где a. = U. - 2U.,. + U.,„, b. = -3U + 4U.,.- U.,„.

j j j +1 j +2’ j j j +1 j +2

Далее на каждом шаге h использовалось разложение экспоненты в ряд expU x ~ (1 + U x - U .) exp U и аналитические решения упрощенных таким образом интегралов.

Результаты расчетов приведены в виде графиков на рис. 1-5, a = r 31 Х _д - относительный размер зонда.

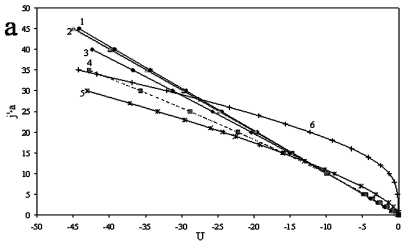
Рис. 1. Зависимости величины j' • а от безразмерного потенциала U в пренебрежении ионизацией (радиальная теория): а) сфера: 1 - а = 0,0001; 2 - а = 0,001; 3 - а = 0,01; 4 - а = 0,1; 5 - а = 1,0; 6 - а = 10;

b) цилиндр: 1 - а = 0,0001; 2 - а = 0,001; 3 - а = 0,01; 4 - а = 0,1; 5 - а = 1,0; 6 - а = 10

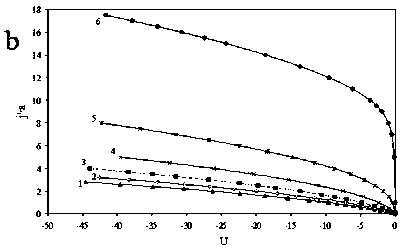
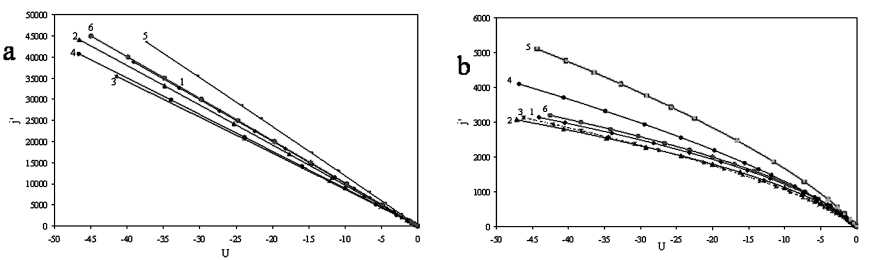
Рис. 2. Зависимости величины j' от безразмерного потенциала U для размера зонда а = 0,001:

а) сфера: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 0,5; 4 - A = 1; 5 - A = 5; 6 - радиальная теория без учета ионизации; b) цилиндр: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 0,5; 4 - A = 2; 5 - A = 5; 6 - радиальная теория без учета ионизации

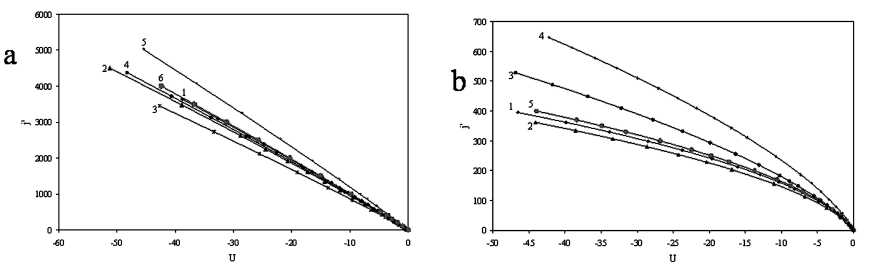
Рис. 3. Зависимости величины j' от безразмерного потенциала U для размера зонда а = 0,01:

а) сфера: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 0,5; 4 - A = 2; 5 - A = 5; 6 - радиальная теория без учета ионизации;

b) цилиндр: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 2; 4 - A = 5; 5 - радиальная теория без учета ионизации

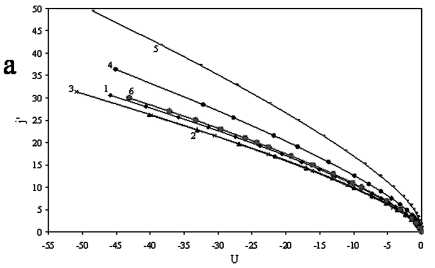
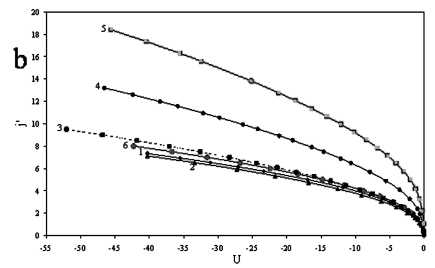
Рис. 4. Зависимости величины j ' от безразмерного потенциала U для размера зонда а = 1,0:

а) сфера: 1 - А = 0,02; 2 - А = 0,1; 3 - А = 0,5; 4 - А = 2; 5 - А = 5; 6 - радиальная теория без учета ионизации; b) цилиндр: 1 - А = 0,02; 2 - А = 0,1; 3 - А = 0,5; 4 - А = 2; 5 - А = 5; 6 - радиальная теория без учета ионизации

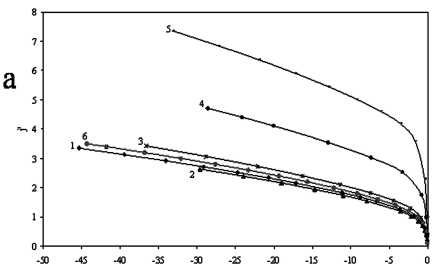
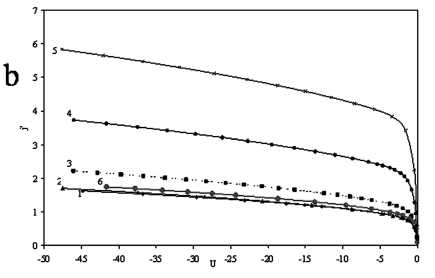
Рис. 5. Зависимости величины j’ от безразмерного потенциала U для размера зонда a = 10,0:

а) сфера: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 0,5; 4 - A = 2; 5 - A = 5; 6 - радиальная теория без учета ионизации; b) цилиндр: 1 - A = 0,02; 2 - A = 0,1; 3 - A = 0,5; 4 - A = 2; 5 - A = 5; 6 - радиальная теория без учета ионизации

Для сравнения были проведены численные решения уравнений (1), (2) исходной радиальной теории без учета ионизации в расширенном диа-r пазоне параметра x = —, для чего использова-^d лись более точные аналитические начальные

4                      3 + 0 , 5 a

+ 0 , 6 a  U

,    + (_) ^{3 +} a .

1 + a a

приближения для потенциала на больших рас

стояниях от зонда, учитывающие левые части уравнений (1), (2):

Для цилиндра при a <  0,01 и a <  10 применимы выражения:

j ' = ^0,23 U ^2/3; j ' = 0^{2 + 0,5} a U ^2/3 + 0 , 6.     (15)

aa

IT c ² c ^{2 4} c ^{2 3 C}\ ^u =^-^° ⁺ -   ⁺ 2 F¹

2 x

x

, c = x з j ' з ,

U = - ~t (1 + ^T

2 x⁴     x⁴

c

12 c ²   3 c⁴

2 x ^{6 +} 2 x ⁸)

c = ^{x 2} j ' з .

В [8], [9], [13] использовался только первый член в суммах, что соответствует нулевым левым частям уравнений (1), (2). Следует отметить, что расширение расчетных данных для малых r_з

— является актуальным для диагностики силь-^д норазреженной плазмы. Помимо этого зондовая теория применяется для описания процессов зарядки пылевых частиц в плазме и образования плазменных кристаллов, где размеры частиц r в эксперименте составляют 0,0001 ^ 0,05 —.

^

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Проанализируем результаты расчетов для случая отсутствия учета ионизации в объеме (радиальная теория). Для малого сферического зонда (a <  0,01) для величины безразмерной

плотности ионного тока достаточно хорошо под-

ходит аппроксимация:

., U .    ефз j = — или j з =--- a              rз

^ 0 n 0

M ’

то есть ток на зонд пропорционален потенциалу зонда, корню из концентрации плазмы и радиусу зонда и не зависит от электронной температуры.

При a <  10 хорошо подходит аппроксимирующая формула

При a > 0,1 вычисления совпадают с результатами [8], [9], [13].

В случае учета объемной ионизации, как видно из рис. 2-6, с увеличением частоты ионизации A плотность ионного тока сначала несколько падает и, проходя через некоторый минимум, далее монотонно возрастает. В сферическом случае, например при любых значениях параметра a , зависимость плотности тока от частоты ионизации хорошо описывается следующим выражением:

21 = 1 - 0 , 52 А^т + (0 , 34 +--- a ---) A ^2/3 •       ⁽¹⁶⁾

j ₀'                            10 + 1 , 2 a

Здесь j ₀ ' - плотность ионного тока при A = 0.

Дифференцирование (16) позволяет получить частоту ионизации A _min , соответствующую минимуму плотности ионного тока. При a << 0,1 получаем A _min = 0,5, что соответствует расчетным данным. Для цилиндрического зонда можно предложить аналитическую зависимость 21 = 1 - 0 65 A¹'³ + (0 52 + — a —) A ^2/3.

j 0 '          ’               ’        3 + 1 , 3a ’

Зависимость плотности ионного тока от частоты ионизации в объеме может быть качественно объяснена следующим образом. При малых размерах области возмущения r ₀ (большая частота ионизации) рождаемые вследствие ионизации ионы находятся в сильном поле зонда и быстро уходят на него, создавая большой ионный ток. С увеличением области возмущения путь ионов увеличивается и ионный ток снижается. При больших размерах области возмущения ионный ток снова несколько увеличивается, так как снижается другой, тормозящий эффект ио-

низации – отставание дрейфовой скорости рожденных ионов от средней дрейфовой скорости потока ионов, уже ускоренных полем на больших расстояниях. При A → 0 и, следовательно, x ₀ → ∞ результаты расчетов соответствуют результатам радиальной теории.

Наличие минимума ионного тока может объяснить образование плазменного кристалла. Так, в [3], [5], [6] обнаружены максимумы значений заряда и потенциала пылевой частицы в зависимости от межчастичного расстояния, соответствующие установившемуся межчастичному расстоянию. Это объясняется немонотонной зависимостью ионного тока из плазмы на пылевую частицу. С увеличением радиуса зонда '' a '' глубина минимума ионного тока уменьшается, как и A _min . Это подтверждает нестабильность существования кристаллов с крупными пылевыми частицами.

ЗАКЛЮЧЕНИЕ

Типичное значение параметра '' A '' в разрядах

низкого давления в трубках с радиусом r –

, л                                           ст

A --<< 1 . Однако в пылевой плазме, где потери

r ст заряженных частиц возрастают, этот параметр может существенно увеличиться. По результатам расчетов можно сделать следующие выводы.

• •    Уменьшение размера зонда ниже дебаевского электронного радиуса в обычной радиальной теории приводит к росту плотности тока на зонд обратно пропорционально радиусу зонда. При этом ток на зонд пропорционален потенциалу зонда в сферическом и потенциалу в степени 2/3 в цилиндрическом случаях.

• •    Зависимость ионного тока на зонд от частоты ионизации при всех размерах зонда и любой геометрии немонотонная. С ростом объемной ионизации плотность тока на зонд сначала уменьшается, а затем растет. В пылевой плазме наличие минимума ионного тока на пылевую частицу может объяснять образование устойчивой пылевой структуры.

Работа была выполнена в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009– 2013 годы», контракт 16.740.11.0329.