К расчету динамики установившегося движения выходного звена в волновой реечной передаче

Волновая реечная передача (ВРП) с роликовой рейкой [1] основана на взаимодействии многокулачкового вала с толкателями, контактирующими с выходным звеном – рейкой на линейных участках диаграмм их относительного движения. Количество толкателей в механизме преобразования движения выбирается сдвиг, приведенный момент инерции, динамическая таким, чтобы в зацеплении с роликами рейки одновременно находилось не менее двух толкателей. Это теоретически обеспечивает линейность функции положения выходного звена, малые изменения характеристики приведенной жесткости и равномерное распределение движущих сил по промежуточным звеньям.

Вместе с тем известно, что работа кулачковых механизмов сопряжена с возникновением переменных ускорений на участках разгона и выбега при удалении и приближении толкателей. Переменные ускорения создают переменные силы инерции и динамическая система привода становится нелинейной. Одновременно с переменными ускорениями в системе возникают переменные аналоги скоростей центров масс звеньев, что вызывает переменность работы сил сопротивлений при их движении в механизме. В приводах с подобными механизмами возникает внутренняя виброактивность, снижающая их динамическое качество.

Динамический анализ привода при взаимодействии с механической системой, имеющей переменные параметры (содержащей шарнирно-рычажные и кулачковые механизмы), методом последовательного приближения разработан М. З. Коловским и подробно освещен в научной и учебной литературе [2; 3]. Волновая реечная передача является своеобразным многокулачковым механизмом, в котором исполнительный орган – рейка – перемещается с постоянной скоростью подобно гайке в винтовом механизме. Приводной вал содержит Z кулачков, установленных с фазовым разворотом друг относительно друга на угол ф = 2 п / Z . Промежуточные приводные звенья -толкатели – перемещаются в корпусе механизма в соответствии с диаграммами (рис. 1) [1], взаимодействуя с роликами рейки на ее линейных участках, с фазовым сдвигом. Перемещение толкателей на остальных участках диаграммы происходит без взаимодействия с роликами рейки.

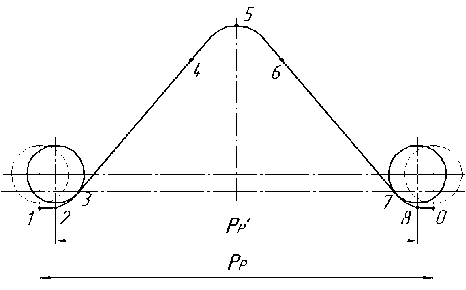
Рис. 1. Диаграмма относительного движения толкателей с участками:

1–2 – нижнего выстоя; 2–3 – разгона; 3–4 – линейного движения; 4–5 – выбега; P p , P′ p – шаг рейки и расчетный шаг.

Участки приближения толкателя симметричны участкам его удаления

Рассмотрим принципиальную схему ВРП (рис. 2). За один оборот кулачкового вала толкатели последовательно войдут в контакт с роликами рейки и каждый переместит ее на величину А Р = P p / Z . Приводной управляемый электродвигатель соединен непосредственно с кулачковым валом через муфту.

Исследование установившегося движения агрегата выполним, воспользовавшись статической характери- стикой двигателя. В этом случае задача сводится к отысканию периодического решения уравнения

• .. 0,5 ■ J ( q ) . ₇                .              .

J пр ( q ) q +-----,        ( q )² = Q д _м ( u , q ) + T _c( q , q ) ,   (1)

dq где Jпр (q) – переменный приведенный момент инер ции машинного агрегата; Qд.м(u, q) – идеальная характеристика движущего момента, зависящая от напряжения u и скорости ротора q ; Tc(q, q) – приведенный момент активных сил сопротивления.

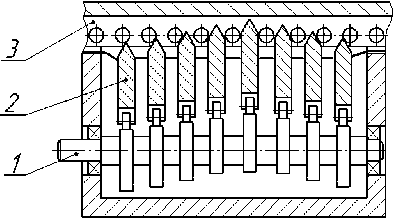
Рис. 2. Схема взаимодействия в ВРП кинематических элементов:

1 – вал кулачковый; 2 – толкатель с клиньями, перемещающийся в направляющих корпуса; 3 – рейка с вращающимися роликами (цевками)

Приведенный момент инерции агрегата определим по зависимости

Z

J пр ( q ) = J д + J к.в + m p V 2.р ■ 10 - 6 + m т ■ 10 - 6 У V 2.т , (2) k = 1

где J _д , J _к . _в – моменты инерции ротора двигателя и кулачкового вала; m p , m _т – массы рабочего органа и толкателя; V _с . _р, V _с . _т – аналоги скорости рейки с рабочим органом и скорости толкателя, мм/рад.

При анализе динамики ВРП следует учитывать две ее особенности.

Первая особенность заключается в симметричности значений аналогов скорости толкателя на участках удаления и приближения за один оборот кулачкового вала (рис. 3).

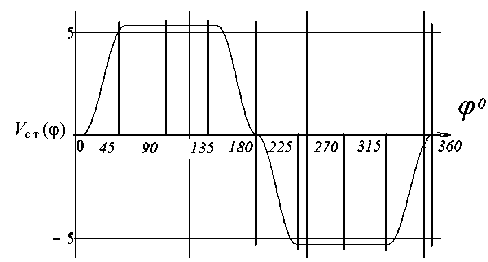
Рис. 3. Аналог скорости толкателя

В соответствии с этой особенностью, а также учитывая возведение в квадрат аналога скорости V _с . _т в зависимости (2), последнее слагаемое можно записать в виде укороченной суммы

Z/2

J пр.т = 2 m т ⋅ 10 ^{- 6} ∑ V с ² .т . (3) k = 1

Второй особенностью ВРП является циклическое изменение инерционных характеристик механизма, связанное со входом в зацепление очередного толкателя. Аналоги скорости соседних зацепляющихся толкателей сдвинуты по фазе. На рис. 3 утолщенными линиями показаны начальные положения аналогов скоростей толкателей, сдвинутых по фазе относительно первого толкателя, находящегося в начальном положении. Это позволяет при расчете приведенного момента инерции толкателей по зависимости (3) рассматривать значения аналогов их скоростей лишь на угловом участке поворота кулачкового вала ϕ p = 2 π / Z , т. е. до момента входа в зацепление очередного толкателя. В связи с этим привод с ВРП можно рассматривать как передаточный механизм, в котором используется мультипликатор с передаточным отношением i = Z /1 : за один оборот вала электродвигателя рабочий вал с кулачковым механизмом как бы вращается в Z раз быстрее. При этом приведенный момент инерции рейки с рабочим органом является величиной постоянной, так как рейка движется с постоянной скоростью, взаимодействуя с толкателями с коэффициентом перекрытия ε_αβ = 2,33 . Аналог скорости рейки V _с . _р связан с аналогом скорости толкателя V _с . _т на линейном участке его движения зависимостью

V _с.р = V _с.т ⋅ tg( α _p) , (4)

где α p – угол клина на толкателе. Для ВРП приве- .

денный момент активных сил сопротивления T c ( q , q ) в зависимости (1) также следует рассматривать как величину постоянную.

Рассмотрим пример расчета неравномерности движения агрегата с ВРП, у которого число толкателей Z = 8, шаг роликов рейки Pр = 20 мм. ВРП обеспечивает тяговое усилие 1 300 Н, скорость перемещения рейки при номинальной частоте вращения ротора электродвигателя nн = 1 000 мин–1 – 0,33 м/с. Масса перемещаемого рабочего органа mр = 100 кг. Привод- ной электродвигатель – ДК1-5,2-1ХХ-АТ с параметрами: мощность W = 0,54 кВт, напряжение U = 110 В, ток при номинальном режиме Jн = 6,5 A, ток холостого хода Jx = 0,8A, сопротивление обмоток якоря R = 2,1 Ом, момент инерции ротора Jд = 4,16E – 3 кгм2, номинальный крутящий момент Тн = 5,2 Нм. Конструктивные параметры ВРП: полный ход толкателей hт = 12,06 мм, ход толкателей при взаимодействии с роликами рейки (активный ход) ha = 8,32 мм, диаметр роликов dр = 5,5 мм, масса толкателя mт = 0,093 кг, момент инерции кулачкового вала Jк.в =1, 6⋅10-4 кгм2.

Расчетные значения аналогов скоростей толкателей для десяти положений на участке поворота кулачкового вала ф _расч = 2 п / Z = 45 ° приведены в табл. 1.

Значения приведенного момента инерции толкателей, рассчитанные по выражению (3), приведены в табл. 2

Значение приведенного момента инерции рабочего органа с рейкой, кгм 2 :

J пр.р ( q ) = m p V с ² .р ⋅ 10 ^{- 6} = 0,001013.

Суммарный приведенный момент инерции привода машинного агрегата с ВРП представим в виде ряда Фурье, принимая за условный период время поворота кулачкового вала на угол ϕ p _асч:

∑ ^{10 ≈} 2π n

J _пр (     ),                       (5)

n = 1       10

≈ где J0 – постоянная составляющая; Jпр – переменная составляющая, определенная как сумма двух гармоник (Jic – гармоника по косинусу; Jis – гармоника по синусу), вычисленных по формулам

1^{10   ≈}   2 π n π n

J _{1 c} = ∑ J _пр()cos();

5n=1

1^{10   ≈}   2 π n π n

J _{1 s} = ∑ J _пр()sin();

5n=1

1^{10 ≈} 2 π n 2

J _{2 c} = ∑ J _пр()cos();

5n=1

1^{10 ≈} 2 π n 2

J _{2 s} = ∑ J _пр()sin().

5n=1

Построим при помощи MathCad графики рассчи-≈ танных Jпр и ∂Jпр(q) /∂q (рис. 4).

Таблица 1

Аналоги скоростей толкателей, мм/рад

№ толкателя	Угловые положения толкателей
	1	2	3	4	5	6	7	8	9	10
1	0	0	0,145	0,564	1,212	2,018	2,892	3,739	4,466	4,992
2	5,261	5,297	5,297	5,297	5,297	5,297	5,297	5,297	5,297	5,297
3	5,297	5,297	5,297	5,297	5,297	5,297	5,297	5,297	5,297	5,297
4	5,297	5,297	5,234	4,871	4,212	3,345	2,385	1,460	0,182	0

	Суммарные приведенные моменты инерции толкателей, кгм2						Таблица 2
J пр.т /10 6	15,5	15,6        15,5	14,9	13,8	13,1	13,0       13,4	14,2	15,0

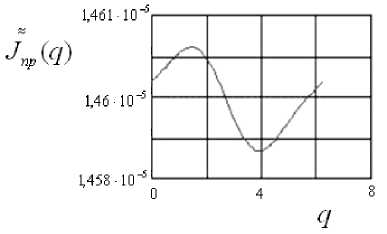
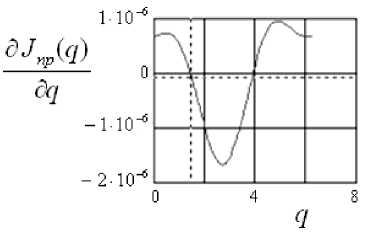
Рис. 4. Характеристики приведенного момента инерции

Уравнение движения машинного агрегата, учитывая постоянство приведенного момента активных сил сопротивления T c ( q , q ) в зависимости (1), запишем в форме

..        ■             =        .. 0,5 5 J ( q ) . ,

J о V- T ( q ) - T = - J пр ( q ) ■ q ---^пр    ( q ) 2 ,    (6)

dq щающего момента L(tocр, t) с использованием коэф-^

фициентов разложения в ряд Фурье J _пр ( q ):

L (и t ) = ^ [ L_l cos( l и t + 1 a _l ],             (8)

i = 1

где l - порядок  гармоники;   Lt = LL+LFs, где v — динамическая ошибка углового положения ■ ротора; Tд(q) – движущий момент, Нм.

Представим движущий момент в виде статической характеристики, рассчитанной по данным двигателя: ■ к

Т д ( q ) = -1 ( U - K 2 ■ 30 ■to / п ) =

R                             (7)

= 40,875 - 0,3405 ■to

Т = F V -tefa ) + F V = c тяг ' с.т ^g V^ap       тр ' с.т

= 5,297 ■ 10 - 3 (1300 ■ tg( a _p) + 175) = 5,06,

L lc = ^{- 0,5} ■ ^Jl5^{l U}2 , L l5 =^{- 0,5} ■ ^JJ ^U2 ; ^Jc , J ^{- коэффи}циенты разложения в ряд Фурье функции J пр ( q ); u = to cZ . Угол a _l определяется с учетом знака

sin a _l =- L⁵- и cos a _l =- L^- . Поскольку значения

производной

d J пр ( q ) d q

на три порядка меньше значе-

ния коэффициентов разложения в ряд Фурье функции J _пр ( q ) (рис. 4), ее учитывать не будем.

где T c – приведенный момент сил сопротивления на рабочем органе и ведущих толкателях, Нм; F тяг – тяговое усилие на рейке, H; F с.т – аналог скорости толкателя; F^ = 175 Н - сила трения на ведущих

Динамическую ошибку скорости в первом приближении определим по выражению [4]

толкателях; K 1 = 0,78, K ₂ = 0,096 - конструктивные параметры; коэффициент при угловой скорости to представляет собой крутизну 5 = 0,340 5 статической

.

v = -Z

l = 1

[ L i sin( l u t + a i +5 1 ]

7 J 2 1 ² U 2 + 5 ²

характеристики двигателя.

Из уравнения (6), полагая в нулевом приближении его правую часть равной нулю, а также что V = 0

и знаки момента сил сопротивления и движущего мо-

мента противоположны, определим среднюю скорость вращения ротора двигателя, с –1 :

s где 5 ₁ = arctg( ) + п .

J 0 l υ

Рассчитанная ошибка скорости вала электродвигателя, а также рабочего органа ВРП представлена графиком на рис. 5.

По максимальному и минимальному значениям ошибки скорости определен коэффициент неравномерности движения рабочего органа ВРП:

^to cр

(40,875 - 5,06)

0, 4305

= 105,18.

V max ^-V min

^to c

0,052 + 0,045

105, 2

» 0,001.

Динамическую ошибку | V |<< tocр определим из (6), представив его правую часть в виде возму-

Итак, предложена методика расчетной оценки неравномерности движения выходного звена волновой реечной передачи – рейки с рабочим органом – на основе метода расчета динамики машинного агрегата с жесткими звеньями, разработанного М. З. Ко-ловским.

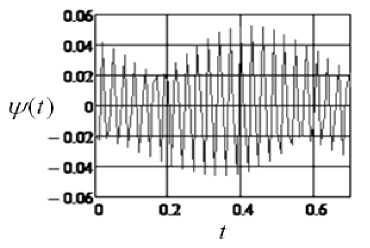
Рис. 5. Динамическая ошибка скорости выходного звена ВРП

В связи с линейной характеристикой скорости рабочего органа в возмущающем воздействии системы привода ВРП приведенный момент активных сил со .

противления T c ( q , q ) в зависимости (1) следует рассматривать как величину постоянную.

В приведенном значении момента инерции передачи следует учитывать его изменение в связи с цикличностью входа в зацепление очередного толкателя, а также частоту возмущающего воздействия от переменного момента инерции – в Z раз превышающую частоту вращения кулачкового вала, где Z – количество кулачковых механизмов в передаче.