К расчету фокусаторов лазерного излучения в дифракционном приближении

С развитием лазерной технологии возник широкий круг задач, связанных с преобразованием оптического излучения, которые нельзя решить с помощью традиционных оптических элементов. Одной из них является задача фокусировки излучения в заданную область пространства с требуемым распределением интенсивности в ней. Для формирования заданного распределения интенсивности используют фокусаторы - специальным образом рассчитанные и изготовленные фазовые пластинки [1]. Разработанная методика расчета фокусаторов [2] основана на приближении геометрической оптики и ориентирована на задачи фокусировки излучения в произвольные кривые. Однако если размеры области фокусировки становятся сравнимыми с размерами дифракционно ограниченного пятна, необходимо учитывать дифракционные эффекты. Иной метод расчета [з] связан с решением нелинейного интегрального уравнения, связывающего распределение интенсивности в плоскости фокусировки с профилем фазы фокусатора. Заметим, однако, что для некоторых областей фокусировки точное решение интегрального уравнения может не существовать. Такая ситуация особенно характерна для трехмерной (объемной) области фокусировки.

В настоящей работе предлагается метод расчета фокусаторов с учетом дифракции. Метод основан на итерационной процедуре поиска такого профиля фазы фокусатора, при котором получаемое распределение интенсивности наиболее близко к требуемому. Пусть в выходном сечении фокусатора (плоскость z=0) излучение характеризуется комплексной амплитудой А (г, z=0):

А(г, 0) = Ао(r)exp[iu(r)],                                          (i)

где и (г)     - фаза поля;

Ао(г) - его амплитуда, которая полагается известной;

Г={х,у} - декартовы координаты в плоскости, перпендикулярной оси 0Z.

Распространение излучения до области фокусировки LSzSL+1, отделенной участком оптически неоднородной среды, будем описывать в квазиопти-ческом приближении:

-,. ЗА    . _ . 2k² , .           а²     а²

21k — = А. А + --- 6пА, Д. = --- + ---.                           (2)

Э2          По             ЭХ2   ЭУ2

Здесь k = ^, X - длина волны излучения, 6п и п₀ - соответственно флуктуации и невозмущенное значение показателя преломления среды, L - расстояние от фокусатора до области фокусировки, длиной 1. Качество фокусировки в заданную область с требуемым распределением интенсивности 1°(г) можно оценивать по некоторому интегральному критерию, например:

J = /ЛАА* - I°||z=Ldar.                                        (3)

(Здесь и далее для простоты рассматривается лишь плоская область фокусировки. Обобщение на объемную область несложно - в критерии J следует добавить еще одно интегрирование по z от L до L+1).

Требуется, подбирая фазу фокусатора u(r), минимизировать функционал J и сформировать тем самым в области фокусировки распределение интенсивности, наиболее близкое к требуемому. Такая постановка задачи обладает рядом важных преимуществ. В частности, она позволяет найти приближенное решение задачи фокусировки в случаях, когда точное решение АА*=1° не существует. Становится также возможным решение задачи фокусировки в заданную область через неоднородную и нелинейную среду с известными неоднородностями показателя преломления.

Поиск минимума J удобно производить одним из градиентных методов [4], в которых по известному градиенту J• {и} минимизирующая последовательность (и } может строиться следующим образом:

Un+1(?) = un(r) - hn • J'{un),                                   (4)

где h - длина шага метода, п Анализируя изменение критерия ДЛ, вызванное малой вариацией Ди, можно показать, что J' имеет вид:

J*[u} = -2Aq[IфI sin(и + агдф)]|2_0,(5)

где "сопряженная" функция ф должна удовлетворять условиям:

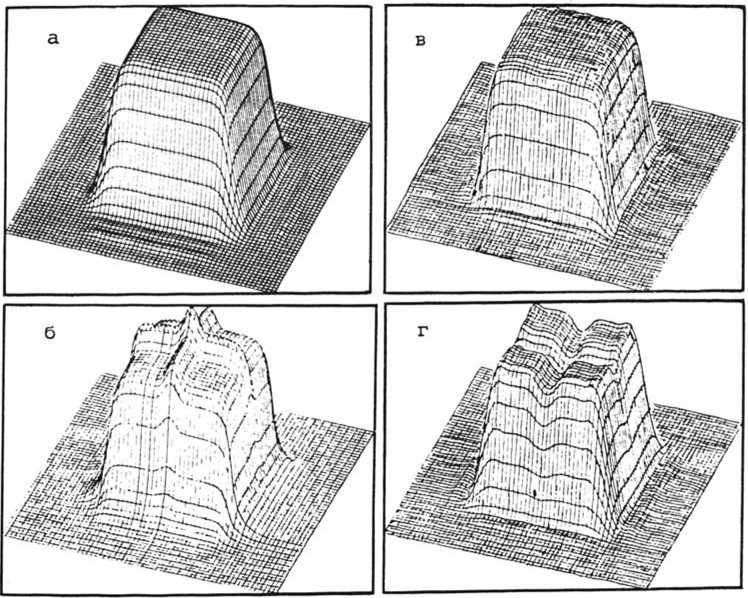
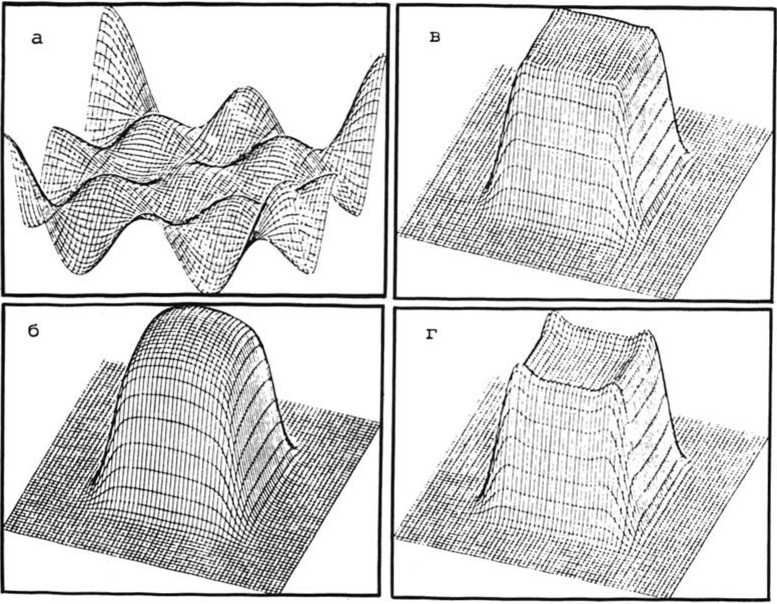
{-21k    = Д. ф + — бпф, 0

9z 1 п0

Ф(г , z=L) = [A*sign(AA* - i0)J|Z=l‘

Таким образом, схема определения оптимального профиля фазы фоку-сатора и (г) заключается в следующем:

• 1)    выбирается некоторое начальное значение фазы и (г);

• 2)    в соответствии с (1) , (2) решается задача распространения излучения от апертуры фокусатора (z=0) до области фокусировки (z=L);

• 3)    используя граничное условие (7) , находят комплексную амплитуду "сопряженной" функции ф(г, L) ;

• 4)    в соответствии с (6) решается задача обратного распространения волны ф и определяется функция ф(г, 0) ;

• 5)    новое значение фазового профиля фокусатора u_n(г) выбирается, например, по формулам (4), (5), замыкая тем самым градиентную процедуру минимизации J.

Уравнения распространения (2), (6) целесообразно решать методом расщепления по физическим факторам [5], с использованием алгоритма быстрого преобразования Фурье. Это делает вычислительные затраты представленной схемы расчета сравнительно низкими.

В качестве примера численно решалась задача создания почти прямо угольного распределения интенсивности 1°(г, z)~exp[-(^—) 1 0 ° о

- (^”Ь г3

—). Среда Ь^

в области L

k*’                  к                            кЬ»

для случая умеренной дифракции (L=O,1L^, 1=0,04L^, L^ = —у - дифракционная длина для заданной ширины апертуры фокусатора Ьо). Заметим, что ширина дифракционно-ограниченного пятна в z=L равна b =b L/L =0,1Ь g о ' g ' о

то есть в 10 раз меньше ширины требуемого распределения интенсивности

• 1° (г). В таких условиях, как видно из рис. 1, удается сформировать

достаточно близкое к требуемому распределение интенсивности во всей об ласти фокусировки.

Перспективным является использование в качестве фокусаторов гибких управляемых зеркал, фазу поля после отражения от которых можно представить в виде: u(r) = 2 a S (г) , где а - сигналы управления, S (г) - функции отклика зеркала,

М - число приводов зеркала. Функционал J^, ста новится теперь функцией сигналов управления а :J_ {а }. Прежняя задача m 2 m фокусировки в область 1°(Г), L

9          9

численно для зеркала, функции отклика которого моделировались функциями

Рис. 1. Фокусировка в объемную область (0,10Lg

Эрмита: S (х) = Н (х/Ь ) • ехр(- х2/2Ь2)(М=4), где Н (х) - полиномы m        am о                  °

Эрмита. На рис. 26, в, г показана интенсивность поля в плоскостях z^, k=l, 2, 3 при оптимальной (обеспечивающей min Jg (ат) ) Фокусировке. Про-fa}

Филь поверхности такого гибкого зеркала изображен на рис. 2а. Таким образом, с помощью гибких зеркал возможно качественное формирование требуемого распределения интенсивности, причем необходимый профиль зеркала остается достаточно плавным.

Отметим, что дифракция ограничивает размеры области фокусировки, в которой еще имеет смысл ставить задачи формирования заданного распределения интенсивности. Так, уже при L=0,5Lg (размеры области фокусировки лишь в два раза больше Ь^) распределение интенсивности АА* значительно отличается от требуемого 1°(г), хотя еще и имеет заметное центральное плато и последующий плавный спад интенсивности.

Рис. 2. Фокусировка в объемную область (0,10Lg