К расчету пластин в условиях плоского напряженного состояния на температурные нагрузки вариационно-разностным методом в функциях напряжений

Одной из причин появления напряжений в теле является неравномерное его нагревание. Температура как в земных условиях, так и в космическом пространстве изменяется ежесекундно. Опасные напряженные состояния возникают необязательно при высоких или низких температурах; опасными должны быть неравномерные изменения температурных воздействий как по области конструкций, так и по времени. Важным случаем температурного воздействия являются моменты входа аппарата и пластин солнечных батарей в тень Земли и выхода из тени. Также в период эксплуатации системы конструкций действует постоянное многоцикловое неравномерное нагревание и охлаждение. Возможны явления усталости материалов, приводящие к локальным разрушениям при сравнительно низком уровне напряжений. Казалось бы, изменения температуры действуют постоянно, а учету дополнительных температурных напряжений, с целью их добавления к напряжениям от силовых факторов, уделяется второстепенное значение (конечно, за исключением оригинальных конструкций). Подход к анализу конструкций односторонний, ограниченный, с пренебрежением к дополнительным факторам, дающим дополнительные напряжения от изменения температуры, а в какие-то моменты они могут проявиться и как основные напряжения, может привести к исключительным нештатным ситуациям. Поэтому работу, посвященную разработке метода расчета конструкций, в частности тонких пластинок, на температурные воздействия с целью исследования напряженного состояния, следует считать актуальной. Tаким образом, требуется разработать подход к решению задач оценки напряженного состояния свободных от закреплений прямоугольных пластин на нагрузки, возникающие при воздействии стационарного тепло- вого потока (температура является функцией координат).

Для решения задачи воспользуемся методом устранения деформаций [1; 2]. В этом методе для изотермического нагружения объемные и поверхностные силы определяются через температурное поле T ( x , y , z ) исходной температурной задачи. Известно, что модуль упругости стали при нагревании уменьшается [2], а модули упругости сплавов при нагревании как уменьшаются, так и увеличиваются (причем в 1,5–2 раза) [3]. Чтобы в разрешающие уравнения не входили упругие постоянные материала [1], краевую задачу формулируют в напряжениях.

Определенное научное содержание работы заключается:

– в полученном выражении функционала Касти-лиано в функциях напряжений, учитывающем изменение температуры;

– алгоритме формирования разрешающей системы уравнений и ее правой части c использованием первой и второй вариаций функционала;

• – составленной программе расчета;

  – расчете напряженного состояния пластинки при неравномерном нагреве.

Рассмотрим вариационную формулировку [4], для которой получим функционал Кастилиано с учетом изменения температуры. В первую очередь, из уравнений равновесия для плоской задачи теории упругости [5] получим вариационное уравнение

-jj(ax 58x + Тxy5Yxy + ay58y )dxdy +jj [X5u + Y5vdxdy + SS

y = b

+ j (ax5 u+Txy5 v) dy

y =0

+ j ( a y 5 v + T * y _X 5 u ) dx

y = b

= 0, (1)

y =0

x =0

где a _x , т , a y - компоненты тензора напряжений; 5s _x , 5y _xy , 5s y - вариации компонент тензора деформаций; X , Y - объемные силы; 5 и , 5 v - вариации вектора перемещений; S - площадь пластинки; a x , т X _y , а * , т^ - заданы на контуре напряжения. Добавив в (1)

Из (8) и (9) перенесем в левую часть произведения объемных сил на перемещения, сложим их и проинтегрируем:

jj ( Xu + Yv ) dxdy = - jjp^ x и +

S                       S ' ^{д x}

закон Гука [2], точнее, вариации деформаций, выра-

женные через вариации напряжений, 5s x = E "^Sa x —ц5а у ) + 5 ( a T )’
	(2)
5s у = 4(5a у — Ц5а x ) + 5 ( a T ), E	(3)
_ 2(1 + ц) я_ 5Y yV             5т уv , xy       E       xy	(4)

дт „ _x    да _у дт _xy )

+-- —u +-- — v +-- — v I dxdy .       (10)

д у     д у     д x J

Интегрирование по частям в правой части (10) по типу

д , - да_х д u Т" ^(a x^u ) = , ^{u + G} x^- , д x д x д x

получим интегральное тождество, содержащее член a T = а T ( x , у ). Из преобразованного уравнения (1) вынесем оператор 5 :

5 s — ГС — Г а — 2 цаа+а +

11 те L x x х у ^у

I s ² E

+ 2(1 + ц ) т 2 _у + 2 E a T ( а _х + а _у ) J dxdx + у = b *

+ jj [ Xu + Yv ] dxdy + j (a*_xu +

Sу у = b x=a-

+ j (аУv+тУxu)dx x=0

д           ^дт yx   ,     д u

(тyxu) =     " + Т ду         ду       ду даёт равенство

...

^: Xy^v ) ^d y    ⁺

= 0.

x =0

Тогда (5) примет вид

5 Э = 0 , (6) где Э - выраженный в напряжениях функционал Лагранжа:

jj^{( Xu} + ^Yv ) ^dxd y = jj f^G x 1 ^ ⁺

S                  S ^{v   д x}

д u

д v

+tvy--+ a,,--+ туз. — yx ду    у ду   xy дx

у = b j (axu+тXyv) dv у=0

x =0 у = b

j K ^{v +т} x =0

*,x^u ) ^dx

у =0

,

которое с учетом геометрических уравнений приводит к jj( Xu + Yv ) dxdy = -1 jjLa x 2 — 2^a x G у +

SES

^+a у ² + ^{2(1 +}ц ^{) т} У x ] ^dxd y ^—

Коши

Э = -[[ — Гаг ² — 2 ца a +G ² +

JJ 2 E L ^{x        x у у}

+ 2(1 + ц ) т 2 _у + 2 E a T ( a _x + а _у ) ] dxdx +

+ jj [ Xu + Yv ] dxdy + j ( a x u + т X _yv ) dy

^S                       у =⁰                     x =0

у = b у=0

x = a

+ j (aУv+тУxu)dx x=0

Рассмотрим вариант исключения из выражения (7) объемных сил X , Y и интегралов на контуре. Для этого формально умножим уравнения равновесия бесконечно малого элемента на перемещения и = и ( x , у ) и v = v ( x , у ) :

да дт „ —xu +-- —u + Xu = 0 , д x     д у	(8)
дт     да -v- v + -^v + Yv = 0. д x д у	(9)

• ^— j ( ^a x^{u +т} Xy^v ) ^d y

у =⁰                     x =0

x = a                     ^у = b

• - j ( ^a У^{V + T}\ x^u ) ^dx

x =0                     у ₌ 0

Подставив (13) в (7), получим искомое выражение энергии деформирования пластинки в напряжениях, называемое функционалом Кастилиано:

Э_к ( а_х , а,,, т_х,,) = f Г—Г а_х ² — 2 ца_хст„ +а, ² + кк x’ ^у’ ^xyd jj 2 e l ^x x х у ^у

+ 2(1 + р ) т X _y + 2 E a T ( a _x +а _у ) ] dxdx ,     (14)

где E = E ( x , у ) - модуль упругости; ц = ц ( x , у ) - коэффициент Пуассона; a = a ( x , у ) - коэффициент линейного температурного расширения материала; T = T ( x , у ) - температурное поле. С приложением функционала Кастилиано краевая задача формулируется так, что из всех возможных напряженных состояний действительное напряженное состояние сообщает функционалу (14) максимальное значение [5].

Введем в функционал (14) функцию напряжений ф ( x , у ) (функцию Эри [6]) без учета объемных сил:

mn

З 2 ( З Э к )) = Ц— i =1 j =1 ^Ei , j

" д ² 3 ₂ фд ² 3 ₁ ф e x ² e x ²

д2ф          _ д2ф          _ д2ф

°x = 3^ ’     °у = 1x2’     Tyx "-Ixdy ’ определяющую искомый функционал

^^^^^^в

д ² З ₂ ф д ² 3 ₁ ф д ² 3 ₁ ф д ² 3 ₂ ф

Э Кw = JJ 2E

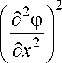
— 2 ц

2     2

д ф д ф дx 2 ду 2

^Гд ² ф) ² ^д У ² J

д ² 3 ₂ фд ² 3 ₁ ф д у ² д у ²

:²    д у ²

m n —2

1 x ² д у ²

■ V22»

- i , j        i =¹ n= -

+

+

д ² 3 ₂ фд ² 3 ₁ ф д x l y д x l y

(18) S n ⁺

^- i ,п

2    2           ( 22

I д ф I           I д ф д ф

+2(1 + ц)        + 2 Ea T+

\8x8y)        ^йх25у

n m —2

+ ZZ (1 +ц )

j =1 §=1 -

д ² 3 ₂ ф д ² 3 ₁ ф 1 x д у 1 x д у

S

j

dxdy , (15)

mn зЭк (З1ф( x, у))=ЕЕ

a T

и сформулируем для краевой задачи с учетом темпе

i =1 j =1

Г д ² 3 ₁ ф

^ д x ²

д ² 3 ₁ ф д у ²

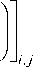
S ,.

ратурного члена, что из всех возможных напряженных состояний находящейся в равновесии пластинки действительное напряженное состояние сообщает (15) стационарное значение.

Чтобы найти напряженное состояние пластинки для формирования разрешающей системы уравнений и ее правой части, предлагается прием использования первой и второй вариаций (15):

Здесь площадки интегрирования S _ap равны:

X _x X _у - во внутренних узлах области; X _x X _у /2 -

в узлах, расположенных на контуре; X _x X _у /4 - в узлах, расположенных в углах пластинки. Дифференциальные операторы в (18) и (19) заменяются конечноразностными аналогами:

—

+ 2(1 + ц )

^{3 Э}к ⁽ ф ^{( x} , У )) = ff^;

E

д ² ф д ² 3ф д x ² д x ²

д ² Зф д ² ф д ² ф д ² 3ф | д x ² д у ² д x ² д у ² J

д^д^ф д у ² д у ²

д ² ф д ² 3ф д x д у д x д у

+ E a T

Г д ² 3ф ^ д x ²

д ² 3к д у ²

dxdy ;

3= Э   " J} E

д ² 3 ₂ фд ² 3 ₁ ф 2 Г д 2 3 ₂ фд 2 5 ₁ ф д^фд^ф ' д ^ д \    Ц д к ² д у ^{2 +} ду² д у ²

Гд^З^ф1   = 3 k ф j+1, j — 23 k ф i, j +S k ф i—1, j l дx2 J.x2, i, j

^Г д ² 3 _k ф )    _ ³ k ^ф i , j +1 ^{— 2 3} k ^ф i , j ^{+ 3} k ^ф i , j —1

I я 2 I =                 л 2                  , дуX

I, j д23 k ф J  = —3 k ф i+1, j+1+3 k фi—1, j+1 — 3 k ф i—1, j +3 k ф+1, j дxду I                    2XXv’ a i ,n д23 k ф I   = —3 k ф i+1, j+1 +3 k ф i, j+1 — 3 k ф i, j—1 +3 k ф i+1, j—1

v дxду J j,§

дЦЗфдХф^     д2З2фд2З1ф ду 2  ду2           дx ду дx ду

dxdy ,

аппроксимации которых легли в основу предлагаемого алгоритма решения задачи.

Применим вариационно-разностную постановку. Выберем на области пластинки (рис. 1) прямоугольную равномерную сетку ю_у = { ( x i = i X _x , у^ = j X _у ), i = 0, 1,..., m , j = 0, 1, ..., n } на отрезках    [0, l x ]

и [0,1у ]. Здесь x = xi и у = yj - узлы сетки; X = L /m и X ,,= l„ / n - шаг сетки, а L и l„ - разме-xx    yy          x y ры пластинки по направлениям осей координат x и у . Введем сетку с узлами ^, п:

ю §п = { ( x § = X x /2 + i X x , У j = X у /2 + j X у ), i = 0, 1,..., m — 1, j = 0, 1, ..., n — 1 } .

Континуальную область в (16) и (17) заменим дискретной. Тогда:

( k = 1, 2).

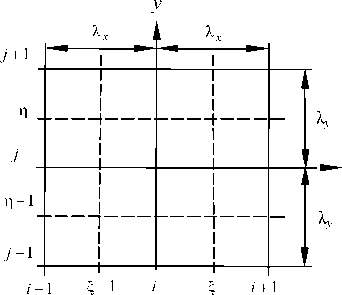
Рис. 1. Конечно-разностная сетка, нанесенная на область пластинки

Для задания функции ф на контуре пластинки используем «рамную аналогию» [5; 6].

Построим алгоритм формирования системы уравнений и правой части . Пусть функционал (15) в дискретной форме содержит вектор p переменных

ф = (ф1,ф2, ...,фp). Тогда (18) содержит вариации вектора 51ф=(б^,51ф2, ...,51фp) и 5гф=(32ф1,52ф2, ...,52фp). Элемент матрицы aij системы линейных алгебраических уравнений вычисляется как aj = 52Эк (51ф, 52ф) = 52(51Эк (51ф, 52ф)) = p 5Эк ( §1ф, §2ф)

5ф i

5 1 ф i

¹2ф к ,

1, при к = i            [ 1, при i = j

, 5,фi = <                   ,

0, при к * i           [ 0, при i * j

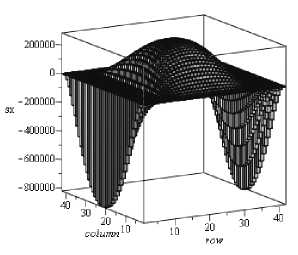
Эпюры напряжений приведены на рис. 3. Для удобства анализа напряженного состояния разделим значения напряжений, приведенных в эпюрах, на введенный в расчет модуль Юнга. Наибольшие нормальные напряжения с _x = - (2/ 5) E a T действуют в области y = ± i y / 2 , а растягивающие напряжения с _x = (1/10) E a T возникают в окрестности у = 0. В более нагретых местах возникают сжимающие температурные напряжения с _x . Условия равновесия элементов пластинки диктуют проявление и растягивающих напряжений с _x . На свободных кромках x = i_x и x = 0 напряжения с _x = 0 .

i = 1, 2, ..., Р ; j = 1, 2, ..., P .             (22)

Цикл (22) из равенства (21) формирует квадратную симметричную относительно главной диагонали матрицу. Соответственно, вектор правой части определяется из (19) циклом

, _        — X _    5 Э Л ⁽ 5 1^ф)

bi = ^ 1 Э л ( 8 1 ^{ф )} = /,            8 1 ^ф i,

1 =1    ^дф i

1, при l = i i = 1, 2, ..., p, 51фi X               .       (23)

[ 0, при i * i

В контурных узлах значения функций Эри известны. В законтурных узлах φ вычисляется по формуле d ф / d v = N , где v - нормаль к контуру рамы, окаймляющей собственно пластинку; N – продольное усилие в раме.

Для расчета пластинки на температурные нагрузки составлена программа расчета на основе пакета Maple. Приведем пример тестового расчета пластинки на изменение температуры по закону T ( x , у ) = T (2 у / i ) ² -такое распределение температуры рассматривается для балок в [1; 2; 7]. Пластинка квадратная в плане размерами i_x = 0,2 м и i y = 0,2 м. Конечноразностную сетку примем с шагом 40 х 40 . Модуль Юнга E = 2 ■ 10 ¹¹ Па, коэффициент Пуассона 0,5.

График распределения установившейся температуры в пластинке по заданному закону приведен на рис. 2.

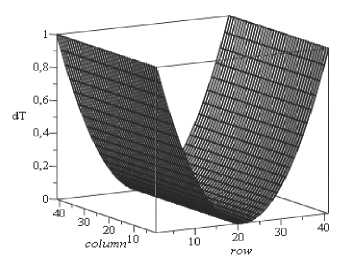
Рис. 2. Эпюра температурного воздействия – график установившейся температуры в пластинке.

Множитель T

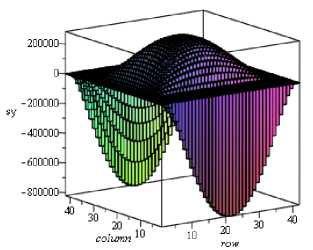
Нормальные напряжения σ _y , наоборот, достигают наибольших сжимающих значений на кромках x = i_x и x = 0, а растягивающих значений - в средней зоне области пластинки. Условия неразрывности деформаций требуют возникновения этих напряжений. Порядок напряжений с y такой же, как порядок напряжений с _x .

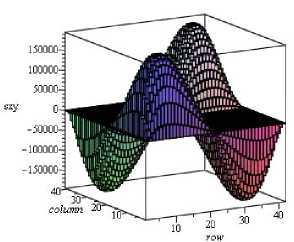
Касательные напряжения достигают значений т _xy = ± (3/40) E a T , наибольшие значения приобретают в областях у = ± i „ / 4, x = ± L / 4 .

yx

а

б

Рис. 3. Эпюры нормальных и касательных напряжений в пластинке: а - с _x ; б - с _у ; в - т _xy (здесь размерность кГ/см ² ; множитель α T )

в

α ET /3

2α ET /3

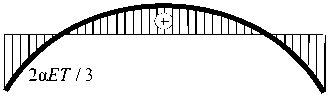
Рис. 4. Эпюра напряжения σ _x в поперечном сечении стержня, полученная методом сопротивления материалов

Характер распределения напряжений σ _x согласуется с характером распределения аналогичного напряжения в стержне температурной задачи, рассмотренной в [7]. Распределение напряжений показано на рис. 4 для стержня шириной b = l_y . Эпюра нормальных напряжений в стержне во всех поперечных сечениях, включая и контур, постоянная. В стержне действие напряжений σ _y и касательных напряжений τ _xy не учитывается.

Таким образом, применение подхода к решению краевой задачи с использованием первой и второй вариаций функционала Кастилиано с конечноразностной аппроксимацией позволили создать универсальный алгоритм расчета напряженного состояния пластинок на температурные воздействия; расчеты напряженного состояния пластинки были выполнены на различных сетках; исследования сходимости решений в напряжениях от сгущения сетки показали достаточность редкой сетки 6 × 6 (т. е. наблюдается достаточно хорошая сходимость напряжений в зависимости от сгущения сетки к напряжениям напряженного состояния, обеспечивающего неразрывность деформаций в дискретной задаче); характер распределения напряжений σ _x согласуется с характером распределения аналогичного напряжения в балках; скромность требуемых ресурсов для реализации позволяет внедрить методику решения рассмотренной плоской задачи в учебный курс теории упругости как добавление к традиционно используемой дифференциальной формулировке краевой задачи в виде бигармониче-ского уравнения неразрывности деформаций.