К расчету среднего значения коэффициента анизотропии листовых материалов

Многие детали современных машин и приборов изготавливаются методами листовой штамповки. При этом используются металлы и сплавы различных структурных групп и марок. Большинство полуфабрикатов (листы, трубы, профили), полученных из этих материалов, обладают явно выраженной анизотропией механических свойств. Особенно она характерна для алюминиевых, магниевых, титановых, бериллиевых и других сплавов [1-2].

Зависимость свойств материала от направления оказывает определенное влияние на технологические процессы изготовления изделий, в том числе и на операции листовой штамповки [3]. Однако, для того чтобы оценить влияние анизотропии, в технологических расчетах необходимо использовать показатели, количественно характеризующие анизотропию свойств. Рассмотрим применяемые в настоящее время показатели анизотропии в области пластического деформирования.

ПОКАЗАТЕЛИ АНИЗОТРОПИИ

Наибольшее распространение получили показатели анизотропии, включающие в себя стандартные механические свойства или их отноше-

ния, определенные для различных направлений материала, например, предложенные Р. Хиллом [4-6]. Он показал, что состояние текстурированного полуфабриката может быть охарактеризовано следующими шестью величинами:

1 1 1 1 2 F = + _ _ Y2 Z2 X2 , 2L R2, 1 1 1 1 2 G = Z2 X2 Y2 2 M = —,    (1) S2 1 1 1 1 2 H = + 2 N = ”2, X2 Y2 Z2 где X, У, Z – пределы текучести при линейном растяжении вдоль главных осей анизотропии; R, S, Т – пределы текучести на сдвиг.

Оценка различий в свойствах среды с помощью таких параметров анизотропии не всегда является точной. Так при испытаниях тонколистовых материалов трудно определить точную величину пределов текучести, то показатели F, G, Н и др. желательно вычислять не по величине пределов текучести, а по деформациям [6].

Для характеристики направления преимущественного развития деформаций при пластическом течении (анизотропии деформаций) широко применяются деформационные показатели анизотропии. Коэффициент нормальной анизотропии R отражает изменение свойств металла в направлении, перпендикулярном к плоскости листового проката, в зависимости от его свойств в плоскости листа. Его определяют по результатам испытаний на растяжение [7], как отношение логарифмической деформации по ширине e_b к деформации по толщине образца e_t :

R = eb- = Ig bo/lg ^ et         b1t1,

где b ₀ , t ₀ , b ₁ , t ₁ – соответственно начальные и конечные значения ширины и толщины плоских образцов. Испытания образцов производятся в зависимости от направления вырезки в листе: вдоль проката R ₀ , перпендикулярно R ₉₀ и под углом 45° R ₄₅ (рис. 1).

Измерение толщины в процессе деформации по формуле (2) не очень удобно, так как связано с возможностью больших ошибок в связи с изме-

нением шероховатости поверхности при растяжении образца, а также с неравномерностью деформации по толщине, вызываемой неоднородностью. Поэтому для оценки анизотропии предпочтительнее использовать коэффициенты Пуассона для пластической области или коэффициенты поперечной деформации Д , представляющей собой отношение логарифмической деформации по ширине e_b к деформации по длине образца e_l [8]:

Д = - eb = lg b0/lg l0 ,        (3)

el        b1l1

где l ₀ , l ₁ – соответственно начальное и конечное значения длины плоских образцов.

Показатели анизотропии всех трех типов пе-

ресчитываются друг в друга и в этом смысле являются равноценными [4-5]:

R = Д

1 — д ,

R

H

- 0    g ,

R

H

-90 -~ F

и

^R 45 =

N

F + G

СРЕДНЕЕ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА АНИЗОТРОПИИ

одинаковы в различных направлениях плоскости листа: Д о = Д 45 = Д 90 ^ 0,5 (плоскость изотропии), и плоскостную анизотропию, при которой коэффициент анизотропии изменяется в плоскости листа в различных направлениях прокатки: Д о ^ Д 45 ^ Д 90 (ортотропный материал).

При оценке влияния анизотропии на штам-пуемость металла и проведения других технологических расчетов часто пользуются осредненны-ми в плоскости листа деф о рмационными показателями анизотропии Д ( R ). Иногда приходится сталкиваться с неточностями в определении этого коэффициента, так существуют различные выражения для вычисления среднего значения коэффициента анизотропии [1, 4-5, 7-8]:

- _ Д0 + Д45 + Д90

Д =-------3-------,(5-а)

-_ ^Д 0 + 2 ^Д 45 + ^Д 90

Д =--------4--------,(5-б)

Д0 + Д22,5 + Д45 + Д67,5 + Д90_

Д =----------,------ 5-------- ,--------, (5-в)

где Д_а - коэффициенты поперечной деформации, измеренные под углом а к направлению прокатки.

Очевидно, что выражения (5) неоднозначно оценивают анизотропию одного и того же листа, как может показаться на первый взгляд. Так, например, в одном и том же приближении по формулам (5-а) и (5-б), когда осреднение идет по трем направлениям, может получиться два различных результата. При этом часто данные выражения представляются как равнозначные [5].

Для получения правильной формулы рассмотрим в совокупности всю плоскость прокатного листа, которую разобьем на направления с шагом 45° (рис. 2, а). Покажем, что все коэффициенты анизотропии можно выразить через три основных: Д 0, Д 90 и Д 45 . В виду того, что тек-

При равенстве приращений деформаций по ширине и толщине д = 0,5 ( R = 1 ) металл изотропен. Различают трансверсальную анизотропию, при которой коэффициенты анизотропии

стура проката имеет три взаимно перпендикулярные плоскости симметрии [8], то среди вырезанных образцов будут идентичные, значения коэффициентов анизотропии которых совпадают:

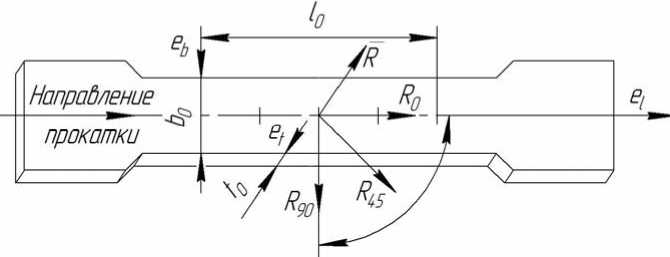
Рис. 1. Схема к расчету коэффициентов анизотропии

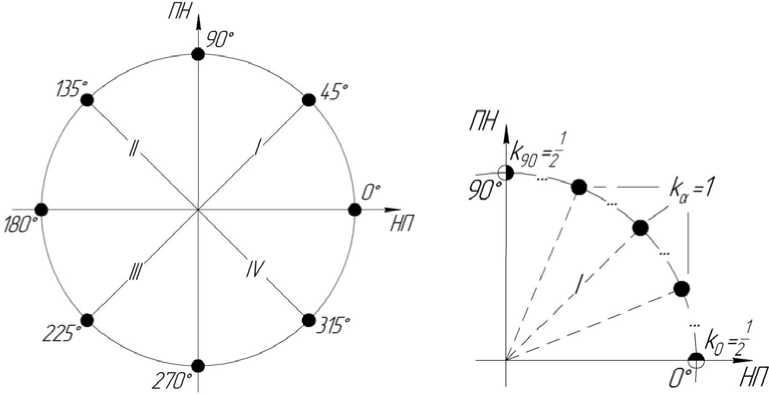
Рис. 2. Расчет среднего значения коэффициента анизотропии

д0 = д180, д45 = д135 = д225 = д315,      (6)

д90 = д270

Среднее значение коэффициента анизотропии во всей плоскости листа определим, как среднее арифметическое коэффициентов поперечной деформации для всех направлений разбиения от 0° до 360°:

- _ До + д45 + ... + д315          _ х д =---------8----------,        (7-а)

или с учетом зависимостей (6):

2До + 4д45 + 2д9о  до + 2Д45 + д9о

д =          8          =        4        . (7"б)

Таким образом, имеем выражение аналогичное (5-б), из которого видно, что вклад (вес) коэффициента Д 45 в среднее значение в два раза больше по сравнению с коэффициентами Д о и Д 90 . Теперь из приведенного примера видно, что формула (5-а) искажает реальную картину, так как утверждает одинаковый вклад коэффициентов поперечной деформации в среднее значение.

Как уже было отмечено выше, все текстурированные материалы обладают симметрией свойств, поэтому на практике достаточно определить коэффициенты анизотропии только для направлений в диапазоне 0-90°. Покажем, как правильно определить среднее значение в этом случае.

Рассмотрим I квадрант координатной плоскости (рис. 2, а), которому принадлежат три направления из разбиения с шагом 45°. При этом было бы ошибкой рассчитывать среднее значение д по формуле (5-а), так как направления 0° и 90° принадлежат этому квадранту не полностью, а только наполовину, и наполовину принадлежат II и IV квадрантам соответственно. Это подтверждается тем, что при сложении всех четырех квадрантов должно получиться восемь направлений. Следовательно, имеем:

~ Д0 + д45 + Т Д90

Д = -------- 2--- ² ----.       (7-в)

Следует обратить внимание на то, что в выражении (7-в) в знаменателе стоит цифра “2”, а не “3”. Дело в том, что в данном случае находится не просто среднее значение трех показателей анизотропии, а среднее взвешенное значение коэффициентов в определенном квадранте. Поэтому в знаменателе записана сумма вкладов (вес) каждого коэффициента д_а в квадранте.

Обобщим выражение (7-в) для случая с произвольным шагом разбиения Д а . Для этого введем весовые коэффициенты к _а , при использовании которых формула для Д будет выглядеть следующим образом (рис. 2, б):

E k Да а • а

— аеm _____

д УА а ае m

где m – это множество всех направлений выбранного разбиения, m = {аг-}, i = 1, n; n - количество участков разбиения квадранта, n = 90°/Да. В формуле (8) каждое из да измерено под углом а, к направлению прокатки: а, = Даг , i = 1, n . Выражение в знаменателе ^ ка — представляет собой общий вес всех ко- ае m эффициентов для данной плоскости, при этом

1                     1      а * 0 ° ;90 °

k0 = k90 = V2 и ка------------>1.

Нетрудно заметить, что формула (8) и формула (7-в) представляют собой одно и то же, что еще раз подтверждает правильность нашего подхода.

В качестве примера рассмотрим использование формулы (8) для вычисления среднего значения коэффициента анизотропии по показателям, измеренным с шагом 22,5° к направлению прокатки. В данном случае: количество участков разбиения n = 90 ⁰ /22,5 ⁰ = 4 ; множество всех направлений m = {0°; 22,5°; 45°; 67,5°; 90°}; общий вес всех коэффициентов ^ k _a = /2 + 1 + 1 + 1 + /2 = 4• аЕ m

Таким образом, окончательно имеем:

-  - Д о ⁺ Д 22,5 ⁺ Д 45 ⁺ Д 67,5 ⁺ - ^Д 9о

Д = 2 --------,------------(9)

Из приведенного примера видно, что формула (5-в) искажает реальную картину, так как утверждает одинаковый вклад коэффициентов поперечной деформации в среднее значение. Хотя из выражения (9) видно, что вклад коэффициентов Д о и Д 90 в среднее значение в два раза меньше по сравнению с остальными коэффициентами.

ВЫВОДЫ

• 1.    Среди применяемых в настоящее время показателей анизотропии наиболее объективными являются коэффициенты поперечной деформации Д , которые, в отличие от коэффициентов Р. Хилла и коэффициентов нормальной анизотропии r , могут быть рассчитаны с высокой точностью для тонколистовых материалов, хорошо

• 2.    Среднее значение коэффициента анизотропии в плоскости листа необходимо определять не как среднее арифметическое значение всех показателей анизотропии по рассматриваемым направлениям, а как среднее взвешенное с учетом веса (вклада) коэффициентов по каждому направлению.

• 3.    Для диапазона измерений в пределах от 0° до 90° к направлению прокатки вклад (вес) коэффициентов Д _о и Д _9о в среднее значение в два раза меньше по сравнению с коэффициентами, измеренным по оставшимся направления выбранного разбиения.

нормированы и обеспечивают преемственность соотношений при переходе из упругой области в пластическую.