К решению задачи об изолированной неоднородности в пористой среде с электрокинетическими свойствами

Одной из важнейших задач фильтрации жидкости в случайно неоднородных пористых средах является замена реальной неоднородной среды на однородную с некоторыми эффективными (макроскопическими) свойствами и эквивалентной реакцией на внешние воздействия (задача гомогенизации). Решение задачи об изолированной неоднородности в неограниченной однородной среде является базовой для многих гомогенизационных схем [5]. В настоящей работе рассматривается задача об изолированной неоднородности в среде, обладающей электро-кинетическими свойствами. Пусть в такой среде имеется замкнутая область V (включение) с дру- гими электрокинетическими характеристиками. Векторы скорости фильтрации жидкости Ui (x) и плотности электрического тока Ii (x) связаны в среде с неоднородностью с векторами градиента давления Ti (x) и электрического поля Ei (x) линейными соотношениями [2] (х - произвольная точка в трехмерной среде)

Ui ⁽ x ) = - kjj ⁽ x ^)Tj ⁽ x ) - “ ij ⁽ x ) Ej ⁽ x X       (1)

Ii ( x ) = -“ jj ( x )Tj ( x ) - a ( x ) Ej ( x )

и удовлетворяют следующим дифференциальным уравнениям д kUk(x) = 0, д kIk(x) = 0          (2)

В уравнениях (1) и (2) обозначено: k j ( x ) - отношение тензора проницаемости к коэффициенту вязкости жидкости, а _у ( x ) - тензор электропроводности и “ ( x ) - электроосмотический тензор, д k = д / д x k . Эти тензоры представляют собой кусочно-постоянные функции координат, принимающие значения k ,, , а ,, , а„ , если x е V , и значения

ООО    J J J j “j,а,если x е V.

Обозначим через V ( x ) характеристическую функцию области V , занимаемой включением:

[1 ( x е V )

V (x) -(3)

[0 (x е V).

Эта функция позволяет представить тензоры ky (x), а, (x), а (x) в виде следующих сумм ky (x) - k“ + k1 V(x), k1 - k„ ij                 ij ij                      ij ij ij

“ij (x) = “j + “j (x Y  “\ = “ij - “j, a (x) = a" + ajV(xX aj = a- aj.

Пусть p(x) и y(x) представляют собой скалярные потенциалы полей Ti (x) и Ei(x): Ti(x)-дip(x),Ei(x)-дiy(x). Подставляя соот-ношения (1) в уравнения (2) с учетом формул (4), можем записать ki0 д iд ,Р(x)+ “j д iд j У( x) = f(xX

“ 0 ^{д д} j P ^{( x} ) ^{+ a} 0 ^д i ^д j ^ ^(x ) = ^{ф ( x} X где обозначено

f ^{( x} ) = ^d V ^{( x} ) [ k ij ^д j P ^{( x} ) + “ j ^д j V< ^x ) ] , Ф ⁽ x ) =^д i V ⁽ x ) [ o j ^д j P ⁽ x ) + a j ^д j И ^{x ) ]} .

Система дифференциальных уравнений (5) эквивалентна следующей системе интегральных уравнений

p ( x ) - p ₀ ( x ) + J G ( x - x ') f ( x ') dx' + j r( x - x ') ^ ( x ') dx ', ^^ y ( x ) - y ₀ ( x ) + J r( x - x ') f ( x ') dx' + J g ( x - x ') ^ ( x ') dx '.

В этих уравнениях p0(x) и y0(x) - поро-вое давление и потенциал электрического поля, которые были бы в среде без неоднородности при заданных условиях на бесконечности, G(x), Г(x), g(x)- компоненты функции Грина системы (7), удовлетворяющие системе уравнений k0 д iд jG (x)+ “j д iд jГ( x) = -^( x),

“ 0 ^д i ^d j^{G ( x} ) ^{+ a} j ^д i ^д j ^{Г ( x} ) = ⁰

ki ⁰ д i д j Г ( x ) + “ ⁰ д i д jg ( x ) - 0,

“ i дд j Г ( x ) + a i ⁰ д i д jg ( x ) - -8 ( x ), где S (x ) - функция Дирака.

Если основная среда изотропна, то есть k j ^{- k} 0 ⁸ у , « - « 0 ⁸ , , ст ® ^- CT ₀ 8 j , то компоненты функции Грина имеют вид

G(x) -г(x) — 7^, А0 4лг          А0 4л r kn 1

g ⁽ x ) ^- —   , ^А 0 ^- k 0 ^CT 0 ^- « 0, r ^- x • А_о 4 л г

Тогда два уравнения (13) и (14) можно записать в виде одного уравнения

Пусть материал включения также изотропен:

k, k18y,  «у «18у, сту CT18y, k1 - k - k0, « - « - «0, стх - ст - ст0.

F ( x ) - F ⁰ ( x ) + J K ( x - x ') M ⁰ L 1 F ( x ') dx ' . (17)

V

Уравнение, аналогичное уравнению (17), можно получить и для пары функций J ( x ) -- [ E i ( x ), I i ( x ) ] в однородной среде с изолированной неоднородностью. Введем для этой цели соотношения, обратные (1), в той же символической краткой форме

F ( x ) - M ( x ) J ( x ), M ( x ) - [ L ( x ) ] ^{- 1} ,

Дифференцируя обе стороны уравнений (7) по координатам, получим

T ( x ) - T ⁰ ( x ) + 1 Ki^x - x ') [ d , T_y ( x ') + d ₂ E j (x ' ) ] dx ' , (13)

E i ( x ) - E ® ( x ) + J K j ( x - x ^ [ d ₃ T j ( x ^ + d ₄ E j ( x ') ] dx ' . (14)

V

L ( x ) -

k ( x ) « ( x )

« ( x ) ст ( x )

Умножая теперь обе стороны уравнения (17) на L ⁰ и используя (18), получим

Здесь обозначено:

^{T 0 ( x} ) ^ i P 0^{( x} X E °^{( x} ) ^ i^ 0^{( x} X

K , ( x ) = ^э i j i ( .

I 4 л г I

L ⁰ M ( x ) J ( x ) - J ⁰ ( x ) +

+ J L ⁰ K ( x - x ^, ) M ⁰ L ¹ M ( x ') J ( x ') dx '. V

С учетом соотношений

L ⁰ M - L ⁰ ( M ⁰ + M ¹ ) = I ⁰ + L ⁰ M 1, M ¹ - M - M ⁰ ,

d 1 - -^( ст 0 k 1 - « 0 « 1),   d 2 - ^( ст 0 « 1 - ст ^Х

^А 0

L 1 M - ( L - L ⁰ ) M - 1 ⁰ + L ⁰ M 1 -- L ⁰ M 1,        (20)

А,

■ 0

где I ⁰ - единичная 2х2-матрица, уравнение (19) можно переписать следующим образом

^d 3 ^- Т" ^{( k} 0 « 1 ^- « 0 ^k 1 X   ^d 4 ^{-    ( k} 0 ^ст 1 ^- « АХ

^А 0

А

Если x е V , то уравнения (13) и (14) представляют собой систему уравнений для определения полей T ( x ) и E i ( x ) внутри V . Если эти поля внутри V известны, то поля T ( x ) и E i ( x ) вне этой области восстанавливаются из уравнений (13) и (14) однозначно. Таким образом, поля T ( x ) и E i ( x ) внутри V являются основными неизвестными задачи. Заметим, что ядро в этих интегральных уравнениях - формально - неинтег-рируемая функция с особенностью | x | в нуле. Для того чтобы придать смысл этому интегралу, будем рассматривать K j ( x ) как обобщенную функцию. Регуляризация интегралов, связанных с действием интегрального оператора с ядром K j ( x ) на гладкие финитные функции, приведена, в частности, в [1].

Введем следующие символические векторы и матрицы:

F ( x ) -

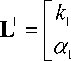
« 1

^ст 1

J ( x ) - J ⁰ ( x ) - J S ( x - x ^, ) L ⁰ M ¹ J ( x ') dx ', V

S ( x ) -

S i, ( x )

S j ( x )

, S i, ( x ) - 8 , 8 ( x ) + K j ( x ).

В общем случае уравнения (19) и (21) могут быть решены лишь численно (эффективный метод численного решения уравнений такого типа описан в [4]). Для включений эллипсоидальной формы и полиномиальных внешних полей эти

уравнения имеют явное аналитическое решение. В этом случае поля внутри включения также полиномы той же степени, что и внешние (теорема о полиномиальной консервативности, см. [3]). В частности, для однородных внешних полей поля F ⁺ - _ T ⁺ , Ei ] и J ⁺ - _U + , I + ] внутри эллипсоидального включения также однородны и определяются выражениями

T ( x ) . ^Ei ( ^x )

F ⁰ ( x ) -

T ⁰ ( x ) . E, °( x )

_M ⁰_- X ^ст    « ⁰

^А 0 _^- « 0    ^k 0

^{K ( x} ) ^-

^K y ^{( x} ) 0

К , ( x )

F ⁺-A F F ⁰ , A F - ( I + AM ⁰ L 1 ) ^{- 1} , (22) J ⁺-A J J ⁰ , A J - ( I + BL ⁰ M 1 ) ^{- 1} ,     (23)

A i

A i

, B -

B,   0

⁰    B i,

, I -

' 8, 0

8 ,

. (24)

Здесь A j и B ij - тензоры с постоянными компонентами. В системе ко орд инат, связанной с главными осями эллипсоида, эти тензоры представляются в виде (по индексу i не суммировать!)

А_л — A S , B_k — S - A (25)

ik i ik ik ik ik

A —

a ₁ a ₂ a ₃ 2

7__________ ,      d ^                , (26)

0 ⁽ a i ⁺ ^ )V ⁽ a ^{2 +} A )(a 2 ⁺ £ )( a 32 ⁺ £ )

Полученные решения покрывают широкий спектр форм неоднородностей: сфера, цилиндр, эллиптическая игла, диск. В частности, для сферической неоднородности A jj — S j 1 3, B j — 2 S j 1 3 и формулы (27) и (28) преобразуются в следующие

где a ₁, a ₂, a ₃ – полуоси эллипсоида. В развернутой форме формулы (22) и (23) имеют вид

T ⁺

D

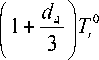
d 2 E 0 3

T ⁺ = D ik 1 [ ( S m + d 4 A m ) T - d 2 A m E m ] ,

Г                       < (27)

E ( — D - k ¹ [- d 2 AX + ( S m + d 1 A km ) E ^ ]

U i = C ^{- 1} [ ( S m + c 4 B m ) U mm - c 2 B .X ] , г"                              n (28)

p — c - [- c з B im u m + ( s m + c B km ) i m ] .

Здесь обозначено

Dk — (Sp + d 1 Ap)(S_pk + d 4 A_pk ) - d 2 d 3 ApApk , (29) C, = (S + c,B )(S , + c.B , A — c^c.B В ,, k p 1 p pk 4 pk 23 p pk ,

E _z⁺— 1 - d ³ T ⁰ +| 1 + d ¹ | E 0

' D Г 3 '    (     3 J '

D _— 1 + ^d 1 ^{+ d} 4 + ^k 1 ^£ 1 ^- « 1

3         9 A 0   ,

c i    k 0 ^S 1    « 0 ^ 1,

c 2    ^ 0 ^ 1   ^k 0 P i ,

c 3    ^ 0 ⁵ 1    ^CT 0 P i ,

c 4 = ^ 0 ^ 1 - « 0 P i ,

и ⁺ — £ 1 1 + 2 c 4 1 и⁰ —c ² 1⁰ , i    c L(       3 J i 3 i _

I ⁽ —--- c ³ U 0 +| 1 + A c ¹ 1 1 0 ,

' C Г 3     ' (      3 J ' _

^{C — 1 +} f( c 1 ⁺ c 4) ⁺ 14 ^A 0( ^S 1 ^K 1 ^- P ² ).

s ₌ £ - £ 1

¹ A A _o, kk ^ = - ”,

¹ A  A 0

о _ «

P1 — лл ,

AA

A — k£ - a ² .

Таким образом, при равенстве «совместной» постоянной a нулю полученные формулы распадаются на известные решения о неоднородности в среде с гидравлической и электрической проводимостями.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ на 2012–2016 гг.

ON PROBLEM SOLUTION OF ISOLATED INHOMOGENEITY IN POROUS MEDIUM UNDERGOING ELECTROKINETIC PHENOMENA