К решению задачи структурно-параметрического синтеза автоматических регуляторов технологических процессов

Актуальность задачи выбора и настройки автоматических регуляторов. Задача качественного построения автоматизированной системы управления технологическим процессом (АСУ ТП) предполагает решение вопросов выбора и настройки автоматических регуляторов, задействованных в различных контурах системы. Несмотря на солидный «возраст» этой проблемы, в ее решении еще имеются достаточно «темные» моменты и требующие дальнейшего развития вопросы. Для подтверждения актуальности и значимости этой проблемы и для настоящего времени укажем, что вопросы выбора и настройки автоматических регуляторов рассматривались и рассматриваются в достаточно представительном списке работ, указанном в [1]. В данных работах предлагаются и анализируются различные способы структурно-параметрического синтеза систем автоматического регулирования (САР), значительная часть работ посвящена настройке ПИД-регуляторов, их модификациям и вопросам их реализации. В 2000 г. только на одном семинаре IFAC (International Federation of Automatic Control) было представлено около 90 докладов, посвященных ПИД-регуляторам. Обсуждается и обоснованность применения ПИД-регуляторов, в частности, утверждается, что П-, ПИ- и ПИД-алгоритмы «…были получены чисто эвристическим путем» [2, с. 82] и что «…достаточно убедительное формальное доказательство целесообразности их применения… до сих пор получить не удалось» [2, с. 24]. Актуальной считается проблема адаптации настроек автоматических регуляторов технологических процессов [3], что совсем не значимо для САР с объектами типа сервомеханизмов. Утверждается, что «…правильно спроектированная, реализованная и налаженная САР на базе ПИД-регулирования может успешно решать 99 % существующих на предприятиях проблем непрерывного управления технологическими объектами» [4, 5], что «…около 90…95 % регуляторов, находящихся в настоящее время в эксплуатации, используют ПИД-алгоритм» [6], что «…ПИД-регуляторы… являются по существу единственными регуляторами, используемыми на практике в системах автоматического управления технологическими процессами» [7]. При этом отмечается, что «…вопреки распространенному представлению, ПИД-регуляторы являются далеко не простыми в настройке» [7]. При решении задачи синтеза САР промышленные объекты управления обычно представляют с помощью следующих типовых передаточных функций:

1 k                        k

-— ехР(-тобp), т об exP(-To6p), ----2-----exP(-To6p), тоб p             тоб p+1             a 2 p + ai p + 1

где kоб, Тоб, тоб - соответственно коэффициент передачи, постоянная времени и время запаздывания объекта, a1, a2 – коэффициенты дифференциального уравнения объекта, p – комплексная переменная.

В учебной литературе по-прежнему базовое место занимает графоаналитический метод расчета настроек ПИД-регуляторов промышленных объектов, детально разработанный в свое время

В.Я. Ротачем [2]. Качество переходных процессов здесь оценивается линейным интегральным критерием, который вообще-то пригоден только для монотонных и знакопостоянных процессов. Это главный недостаток метода, который пытаются компенсировать введением ограничений на запасы устойчивости САР. Утверждается, что это гарантирует достаточно интенсивное затухание переходного процесса, что «…ограничение на запас устойчивости делает процессы регулирования слабоколебательными, площадь под их графиками может быть достаточно точно оценена линейным интегральным критерием» [3]. Тем не менее, это все-таки не исключает его колебательный характер, поэтому линейный интегральный критерий по-прежнему будет оценивать его качество достаточно приближенно. На наш взгляд, распространенность метода обуславливается тем, что задача отыскания минимума линейного интегрального критерия по параметрам настройки регулятора из ПИД-семейства до конца решается аналитически и получаемые ответы хорошо известны. Если же использовать модульный или квадратичный интегральные критерии качества переходных процессов, то введение указанного ограничения на запас устойчивости в подавляющем большинстве случаев будет достаточно излишним. Исключения, по-видимому, составляют случаи, когда требуется предельно высокая точность идентификации математической модели объекта управления (например, случаи применения регуляторов Ресвика и Смита). Получение ограниченных значений таких критериев уже само по себе является свидетельством устойчивости САР, а их минимизация, понятно, только увеличивает его запас. Однако, несмотря на это, существует мнение, что ограничение на запас устойчивости все-таки «…должно быть выведено из подынтегральной функции и задано явно» [8].

Недостатки метода расчета настроек ПИД-регуляторов по минимуму линейного интегрального критерия обусловили появление работы [9] сотрудников Московского энергетического института, как нам представляется, весьма тесно сотрудничавших с В.Я. Ротачем. В [9] непосредственно отмечено, что качество переходных процессов в САР, настроенных на минимум линейного интегрального критерия, обычно хуже, чем при настройках на минимум квадратичного критерия.

Вместе с тем, отметим, что в обсуждаемой графо-аналитической методике рекомендации по выбору типа регулятора не однозначны, отчетливых разъяснений, почему в данном случае (на данном объекте управления) следует применять именно этот регулятор, обычно нет. Понятно, что все это значительно усложняет задачу синтеза системы.

Известны также решения задачи синтеза САР, представленные в формульном виде для настроек регуляторов [10], обеспечивающих три типа переходных процессов на типовых объектах управления. Однако и здесь нет однозначности и отчетливости рекомендаций, не ясно, как были получены указанные формулы для настроек, остается только предполагать, что это было сделано путем обобщения результатов моделирования и натурных экспериментов.

Отметим также и то, что процедура настройки регуляторов остается еще секретом некоторых фирм, работающих в данной области [4], поскольку (процитируем еще раз) «…ПИД-регуляторы являются далеко не простыми в настройке» [7]. Об актуальности и значимости этой проблемы свидетельствуют, например, и данные компании Honeywell, которая провела обследование 100 000 контуров регулирования на 350 предприятиях, принадлежащих различным отраслям промышленности, согласно этим данным 49–63 % САР работает с плохими настройками [11].

В литературе рассматриваются вопросы применения так называемых фази-регуляторов в системах автоматизации технологических процессов. Привлекательность этой идеи основана на том, что объекты, трудно поддающиеся математическому описанию, довольно часто успешно управляются человеком-оператором, который, вообще говоря, формулирует (и, конечно, реализует) свои действия достаточно не четко. Обсуждая перспективность применения таких регуляторов, ограничимся цитированием только того, что высказал на этот счет проф. В.Я. Ротач: «…фази-регуляторы… являются обычными четкими регуляторами. Поскольку квантование только ухудшает качество управления, то… следует считать снятым вопрос о преимуществах таких регуляторов перед традиционными четкими непрерывными регуляторами» [12], что фази-регуляторы являются «…обычными неизвестно зачем усложненными детерминированными регуляторами» [7].

Солидное количество недостатков отмечается и у регуляторов, построенных с помощью нейронных сетей, поэтому не следует ожидать их широкого применения для управления технологическими процессами в ближайшем будущем.

В настоящее время интенсивно разрабатываются процедуры синтеза регуляторов методами H ” -теории [13, 14]. Однако H ” -теория применима для объектов типа сервомеханизмов.

Известен также метод обратной задачи динамики для синтеза систем управления [15].

Таким образом, все вышеизложенное свидетельствует о заметной незавершенности, о том, что необходимо найти ясные и недвусмысленные ответы на еще многие вопросы, казалось бы, уже решенной проблемы выбора и настройки автоматических регуляторов.

Синтез регуляторов по передаточной функции замкнутой системы. В работе [16], как нам представляется, удалось получить некоторое формальное обоснование целесообразности применения ПИД-регуляторов, здесь задача решалась методом выбора передаточной функции замкну той системы в виде Wзс(p)=—-— ехр(-тобp), где 9 - некоторая постоянная времени, а параметр 9 p + 1

т _об приравнивался ко времени запаздывания объекта управления. Выбор указанного вида эталонной передаточной функции замкнутой системы достаточно детально обоснован в [1, 16]. Недавним подтверждением целесообразности такого выбора является и работа [9], в которой, в частности, величина 9 называется «...постоянной времени сглаживателя».

В результате применения данного подхода получили, что для объектов первого типа переда-T точная функция квазиоптимального регулятора будет равна W (p)=—об—, т. е. близким к р      тоб +9

T идеальному является П-регулятор с коэффициентом передачи к = —об—. Для объекта второ-р тоб +9

го типа квазиоптимальным будет ПИ-регулятор, его передаточная функция будет иметь вид

W p ( p ) =

^T об

1 + -1

к об ( т об +9 ) L    Т об P J

. Передаточная функция регулятора для объекта третьего типа будет

такой W _p( p ) =

a ₁

^k об⁽ Т об ^{+ 9 )} L

1 + — 1- + a ²- p , т. е. целесообразно применение ПИД-регулятора. Та- a 1 p a 1

ким образом, было и установлено, что для каждого конкретного объекта управления, принадлежащего множеству типовых динамических объектов, целесообразно применение конкретного регулятора из ПИД-семейства с конкретными настройками. В результате задача структурнопараметрического синтеза автоматических регуляторов локальных контуров становится однозначно решаемой как по структуре регуляторов, так и по их настройкам.

При этом для формализованного выбора постоянной времени 9 рекомендуется следующее соотношение 9=———, где t¥ - время регулирования. Естественно, что при этом следует зада-(5 * 6) Р вать реально достижимую длительность переходного процесса. Если канал регулирования достаточно инерционный, то, как это следует из вышеприведенных формул для настроек регуляторов, малые значения параметра 9 приведут к весьма большим, реально недостижимым значениям управляющего воздействия.

Исследование устойчивости и качества систем. Для полноты исследования предлагаемого способа решения задачи синтеза рассматривался вопрос о качестве переходных процессов в сконструированных указанным образом системах и о грубости этих структур и настроек. В рабо тах [17, 18] указанное исследование проведено для объекта Wоб(p)=—-—ехр(-тобp) с регулято-

T об p

T ром W (p)=—об— . Аналогичные исследования для объекта Wc6(p) = Р      Тоб + 9

k об

^Тоб P ^{+ 1}

ехр( -^т об P ) с РегУ-

лятором W _p( p ) =

^T об

1 + -1

к об ( Т об +9 ) L    Т об p J

и для объекта W^p ) =

k об

a 2 p ² + a 1 p + 1

ехр( -Т об P ) с РегУля^-

тором W _p( p ) =

a ₁

^k об^{( Т} об ^{+9 )} L

1+——+ a ² p проведены соответственно в работах [19, 20]. a 1 p a 1

Для исследования устойчивости и анализа качества переходных процессов в каждом случае разработаны по две компьютерные программы: одна для анализа переходных процессов при возмущении по заданию, а другая – при возмущении со стороны регулирующего органа. В каждой из разработанных программ предусмотрен ввод параметров объекта, а также и параметров настройки регуляторов. Каждая из программ осуществляет не только построение графика переходного процесса, но и определяет перерегулирование σ и время регулирования tР , а также вычис- tК

t К

ляет значения критериев I ₁ = ∫ I ε ( t ) I dt , I ₂ = ∫ ε ² ( t ) dt , где t _К

– конечное время оценки качества

переходного процесса, ε – ошибка регулирования. При этом время регулирования t _Р определялось как время, по истечение которого отклонение регулируемой величины от задания не будет превышать 5 %. Интегрирование дифференциальных уравнений объектов управления осуществлялось методом Рунге –Кутты с погрешностью, пропорциональной пятой степени шага по времени. Для компьютерного использования алгоритм регулирования представляли в дискретной форме, при вычислении интеграла применяли метод трапеций. С целью сокращения объема необходимых вычислений использовали рекуррентные формы дискретного представления алгоритмов ПИД-регулирования. В программах предусматривается ввод нижнего и верхнего пределов изменения регулирующего воздействия. Варьировались как параметры объекта управления, так и параметры настройки регуляторов. Границы области устойчивости, где это представлялось возможным, отыскивались аналитическим методом, в других случаях устойчивость САР оценивалась численным методом по кривым переходных процессов.

Во всех случаях установлено, что рассматриваемый метод синтеза промышленных САР, позволяющий однозначно выбирать как структуру, так и параметры настройки регулятора, обеспечивает приемлемое качество переходных процессов и достаточный запас устойчивости системы при довольно заметных по размерам вариациях параметров объекта управления и погрешностях задания настроек регулятора.

В работе [9] передаточная функция оптимального регулятора также определяется по передаточной функции замкнутой системы вышеуказанного вида. При этом утверждается, что аппроксимация методом наименьших квадратов амплитудно-фазовой частотной характеристики (АФЧХ) найденного таким образом оптимального регулятора АФЧХ ПИД-регулятора обеспечивает минимизацию квадратичного критерия качества переходного процесса, что достаточно удивительно. Причем никаких прямых доказательств этого в [9] не приводится. Кроме того, при таком подходе получается, что для объекта любого типа субоптимальный регулятор один и тот же – это ПИД-регулятор, что является достаточно спорным вопросом. Используется графо-аналитическая процедура, в настоящее время недостаточно удобная и недостаточно точная, кроме того, нужный диапазон частот отыскивается эвристическим способом. В связи с этим утверждение авторов работы [9] о том, что оптимизация настройки регуляторов по квадратичному критерию «…не нашла широкого применения из-за необходимости итерационного поиска оптимальной точки» становится неубедительным преимуществом метода данной работы. Возникает также вопрос: почему бы не решать задачу, используя непосредственно описание САР дифференциальными уравнениями? Всем хорошо известно, что переходные функции (кривые разгона), передаточные функции, АФЧХ и дифференциальные уравнения – это только разные формы представления динамических свойств и характеристик систем и их элементов. Частотные методы разработаны в период, когда не существовало возможности прямого решения проблемы оптимизации настройки с помощью компьютерной математической модели САР и численных методов нелинейного программирования. Частотная методика является графо-аналитической, в ней используется ряд допущений, кроме того, как правило, велика трудоемкость применяемых процедур. К тому же, точность такой настройки контуров регулирования уже нельзя признать удовлетворительной. В настоящее время предпочтительнее использовать формальные компьютерные алгоритмы параметрической настройки, разработанные на основе достаточно точных математических моделей САР и численных методов оптимизации. Вопросы достижения требуемой точности настройки и уменьшения объема необходимых графических построений и сопутствующих им «ручных» вычислений при этом автоматически снимаются.

Численные методы расчета настроек регуляторов. В связи с утверждением работы [9] о том, что оптимизация настройки регуляторов по квадратичному критерию является, якобы, затруднительной «…из-за необходимости итерационного поиска оптимальной точки» приводим данные о решениях этой задачи, в частности, в работах [21–23].

В данных работах разработаны процедуры численной оптимизации настроек ПИД-регуляторов по дифференциальным уравнениям объектов управления.

Расчет настроечных коэффициентов регулятора в любом случае должен начинаться с определения динамических параметров объекта управления, поэтому сначала решалась задача его идентификации, которая формулировалась следующим образом: требуется найти такие значения параметров дифференциального уравнения объекта, при которых критерий n

1 3 = ^ [ x ^Э( О - x ( t i )]²

i = 1

будет принимать минимальное значение. Здесь xЭ – экспериментальное значение выхода объекта, x – расчетное значение, определяемое по модели объекта для одинакового входного воздействия, ti – используемые при идентификации моменты времени, n – число экспериментальных точек.

Данную задачу идентификации для каждого типового объекта управления решали с помощью программы, реализующей метод покоординатного спуска, получающиеся при этом задачи одномерной минимизации решали с помощью подпрограммы, использующей метод золотого сечения. Причем для численного интегрирования дифференциальных уравнений объектов применяли метод Рунге – Кутта, с погрешностью пропорциональной пятой степени шага по времени. Для этого дифференциальное уравнение объекта предварительно записывали в виде системы дифференциальных уравнений первого порядка, т. е. в нормальной форме Коши. Апробацию разработанных алгоритмов параметрической идентификации проводили по большому набору экспериментальных кривых разгона, приведенных в работах [10, 24]. Во всех случаях были полу-

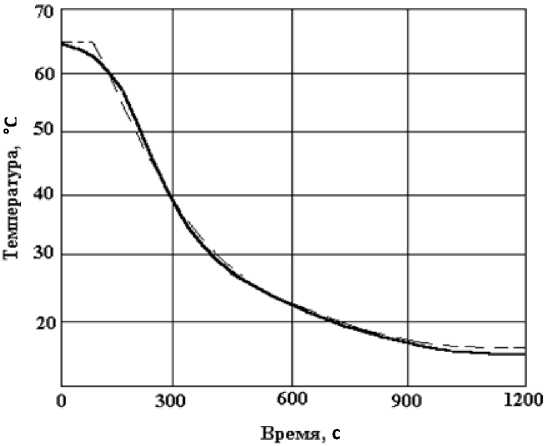
Рис. 1. Расчетная и экспериментальная кривые разгона водо-водяного подогревателя

чены достаточно качественные результаты идентификации. Для примера на рис. 1 приведены экспериментальная и расчетная, т. е. найденная по настроенному дифференциальному уравнению объекта, кривые разгона водо-водяного подогревателя по каналу «расход сетевой воды – температура нагреваемой воды на выходе из подогревателя». Здесь экспериментальная кривая разгона изображена сплошной кривой, а расчетная – штриховой. Подогреватель с наружным диаметром корпуса 108 мм имел 6 последовательно соединенных секций длиною по 4 м каждая. Температуры сетевой и нагреваемой воды на входе в подогреватель составляли соответственно 69 и 14 °С. Расход нагреваемой воды при проведении эксперимента поддерживался практически постоянным и равным 0,664 кг/с, рас- ход же сетевой воды был снижен с 1,14 до 0 кг/с. В данном случае объект управления описывался дифференциальным уравнением третьего типа, найденные численные значения пара-

метров которого таковы: a 2 = 999 с²; a 1 = 256 с; т _об = 62 с; к _об = 43,85 ° С/(кг/с) .

Для данн ого сл учая среднеквадратическое отклонение расчетной кривой разгона от экспериментальной I ₃ / n равно 0,42 °С, что достаточно удовлетворительно.

Разработали также процедуры идентификации динамических свойств объектов управления по переходной функции работающей САР [22]. Необходимость этого объясняется следующим образом.

Широко известно, что динамические свойства промышленных объектов управления, в частности, нагревательных и термических печей по каналу «расход топлива – температура в зоне» существенно изменяются при изменении их режима работы [22]. Особенно сильному изменению подвержен коэффициент передачи объекта, численное значение которого может изменяться в процессе работы печей в несколько раз. Изменчивость динамических параметров объектов приводит к тому, что показатели качества регулирования в системах с неизменными настройками автоматических регуляторов изменяются при изменении режима работы печей. Попытки выявления и использования причинно-следственных связей для отслеживания значений динамических параметров с целью улучшения показателей качества регулирования в целом не решают проблему вследствие существенной нестабильности взаимосвязей [22]. В этих условиях целесообразно периодически в процессе работы печей определять динамические параметры каналов регулирования и оптимизировать параметры настройки автоматических регуляторов, т. е. динамические свойства объекта управления необходимо определять в процессе работы САР по ее реакции на ступенчатое воздействие (переходной функции замкнутой системы) [22]. При этом применяется либо возмущение по заданию, либо возмущение со стороны регулирующего органа (по нагрузке). Последнее воздействие может быть организовано путем подачи по каналу интерфейсной связи команды перевода контура регулирования в режим ручного управления с последующим быстрым изменением положения регулирующего органа и немедленным возвратом в автоматический режим. Понятно также, что при этом следует использовать математическую модель всего контура регулирования.

Следует заметить, что разработанные алгоритмы идентификации достаточно просто модифицируются для случая, когда вместо критерия I ₃ требуется минимизировать сумму модулей разностей расчетных и экспериментальных значений координаты x , а также для случая минимаксной задачи: это когда требуется минимизировать максимальное отклонение расчетных значений от экспериментальных данных. Критерию I ₃ следует отдавать предпочтение в связи с тем, что оценки параметров, найденные посредством минимизации такого критерия, как известно, являются наиболее правдоподобными. Кроме того, использование интегральных критериев идентификации потребует незначительных изменений в программах.

Задачу отыскания оптимальных параметров настройки ПИД-регуляторов также решали методом покоординатного спуска. Причем для компьютерного использования уравнения регуляторов представляли в дискретной форме, при вычислении интегралов применяли метод трапеций. С целью сокращения объема необходимых вычислений использовали рекуррентную форму дискретного представления уравнений регуляторов [21]. Разработанные компьютерные программы решают задачу поиска оптимальных параметров настройки регуляторов как для случая возмущения по заданию, так и для случая возмущения по нагрузке. Причем при разработке программ использовали как критерии качества настройки контуров I 1 и 1 2 , так и критерий 1 4 = с 1 ст + c 2 t Р , где с 1 и c ₂ - весовые коэффициенты. Заметим, что перерегулирование ст для случаев возмущения по заданию и возмущения по нагрузке определяется различным образом [2, 10]. При тестировании разработанных программ получили вполне приемлемые результаты. Для примера ниже приведены данные по настройке ПИ-регулятора, работающего с объектом, динамические свойства которого конкретно представляются дифференциальным уравнением третьего типа с a ₂ = 2,366 с²; а 1 = 1,750 с; Т об — 1,000 с; к об — 0,800 Па/% хода ИМ (канал «положение дымового шибера - давление в рабочем пространстве печи»). Здесь ИМ – исполнительный механизм. Оптимальные по критерию I ₂ настройки ПИ-регулятора при возмущении по заданию таковы: коэффициент передачи к _р — 1,175 % хода ИМ/Па ; время интегрирования Т_и — 2,963 с . Кривая переходного процесса в настроенной таким образом САР приведена на рис. 2.

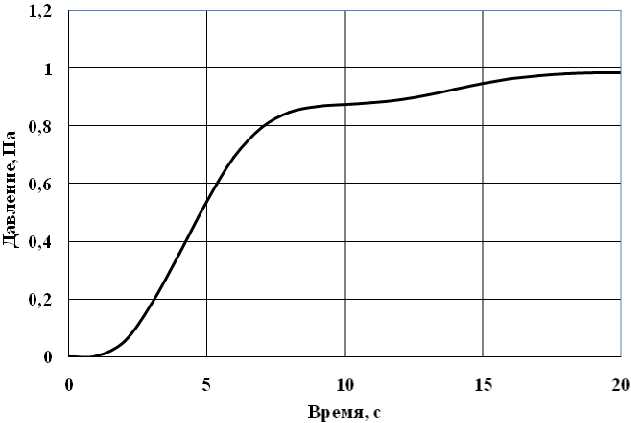
Рис. 2. Переходный процесс в САР

Таким образом, разработан комплекс программ для численного расчета систем автоматического регулирования. Комплекс включает следующие программы:

• 1)    для определения оптимальных значений параметров дифференциального уравнения объекта управления как по экспериментальной кривой разгона, так и по передаточной функции замкнутой САР;

• 2)    для расчета оптимальных параметров настройки ПИД-регуляторов как при возмущении по заданию, так и при возмущении по нагрузке;

• 3)    для расчета переходного процесса и показателей его качества в системе автоматического регулирования как при возмущении по заданию, так и при возмущении по нагрузке.

Данный комплекс программ значительно облегчает процедуру и повышает точность расчета и может быть использован как при выполнении курсовых и дипломных проектов, а также для настроек промышленных систем автоматического регулирования.

Заключение. Разработаны численные процедуры для определения оптимальных значений параметров дифференциальных уравнений объектов управления как по экспериментальным кривым разгона, так и по экспериментальным переходным функциям замкнутых САР. Предложен метод структурно-параметрического синтеза автоматических регуляторов по эталонной передаточной функции замкнутой системы, который дает однозначные ответы на следующие вопросы: какой регулятор следует использовать для данного объекта управления и каковы должны быть его настройки. Показано, что сконструированные таким образом САР обладают должными запасами устойчивости и приемлемым качеством переходных процессов. Поэтому данный метод синтеза рекомендуется для практического использования. Для случая неформализованного выбора типа регулятора (по терминологии [8] экспертного метода выбора структуры регулятора) из ПИД-семейства при конструировании САР разработаны процедуры численной оптимизации его настроек по дифференциальному уравнению объекта управления.