К решению задачи управления направлением тепловых потоков в сплошных средах

Во многих отраслях техники управление направлениями тепловых потоков является задачей, обеспечивающей повышенные эксплуатационные и прочностные характеристики изделия. Таковыми являются, например, теплообменники, теплозащитные покрытия, системы охлаждения и т.д. Можно привести достаточно много примеров, в которых целенаправленно меняется интенсивность тепловых потоков в нужных направлениях. Одним из мощных средств решения такой задачи является применение слоистых конструкций, в которых отдельные слои выполняются из материалов с требуемыми теплофизическими характеристиками [1, 2]. Наряду с этим известно, что в практике создания слоистых конструкций зачастую технологически не удается обеспечить качественное соединение слоёв, что придаёт границе раздела слоёв специфические теплофизические характеристики. В таких случаях налицо естественное нарушение идеальных условий для тепловых потоков. Такие нарушения могут быть обнаружены специальными методами, например, методами томографии, термографии [3]. Особо важным решение проблемы управления тепловыми потоками в сплошных средах становится при разработке конструкций с памятью. В связи со сказанным представляется, что изучение влияния различных факторов на характер распространения тепла в слоистых средах представляется актуальным. Особое значе-

ние эта проблема приобретает с развитием нанотехнологии [4].

Результаты настоящих исследований могут инициировать постановку и решение задач управления направлениями тепловых потоков при решении многих технических задач. В настоящей работе поставлены и решены задачи об идеальном и неидеальном теплообмене между слоями, которые могут внести определенный вклад в решение проблемы управления тепловыми потоками.

Впервые задача с неидеальным теплообменом в слоистых структурах рассмотрена в [5]. В работе было показано, что условие неидеального теплообмена приводит на границе раздела слоёв к разрыву (скачкам) не только тепловых потоков, но и значений температур в сплошной среде. Актуальность проблемы подтверждается тем, что в литературе появляются исследования в аналогичном направлении. Например, в [6] получено аналитическое решение нестационарной одномерной теплопроводности для двух полупространств при неидеальном тепловом контакте на поверхности их сопряжения. В настоящей работе задача рассматривается в более общей постановке - в постановке, позволяющей управлять направлениями тепловых потоков, в том числе, за счет обеспечения условий неидеального теплообмена.

При изучении теплообмена в телах слоистой структуры при переходе от k-ого к (k+1)-ому слою обычно выполняются условия совершенного теплообмена, когда на границе раздела слоёв принимают условия равенства не только температур, но и тепловых потоков [7]

Tk = Tk+1, XkдTk/dv = -Xk+1 д Tk+1 /д V, k = 1, 2 ,…, М. (0.1)

Здесь X k — коэффициент теплопроводности в материале k-ого слоя, v — направление нормали к поверхности раздела. При выполнении ус- ловий (0.1) температура изменяется непрерывно при переходе от слоя к слою, в то время как градиенты температур в слоях отличаются в отношении теплопроводности смежных слоёв.

( д T^k / д v )/ ( д T^k+1 / д v ) = - X ^k+1 / X ^k (0.2)

Если условия (0.1) нарушены, то, в отличие от условий совершенного теплообмена, на границе раздела слоёв должны быть приняты условия другого типа. В частности, одним из таких возможных условий может быть условие конвективного теплообмена между слоями, использованное в [5, 7]

X ^k д T k / д v = - a ^k ( T k - T^k+1),

X k+1 д T k+1 / д v = a k+1 ( T^k+1 - T k ). (0.3)

Здесь a ^k характеризует теплообмен между k+1-ым и k-ым слоем, а a ^k+1 - регулирует количество тепла, которое переходит от k-ого слоя в k+1-ый.

Градиенты температур на границе раздела слоёв при не идеальном тепловом контакте слоёв согласно условиям (0.3) отличаются в отношении теплопроводности смежных слоёв.

( д T^k / д v ) / ( д T^k+1 / д v ) =

= ( X ^k+1 a ^k) / ( X ^k a ^k+1). (0.4)

Из сравнения соотношений (0.2) и (0.4) следует, что тепловые потоки будут одинаковыми только в случае равенства коэффициентов теплообмена ( a ^k = a ^k+1). Таким образом, условия совершенного теплообмена (0.2) при переходе от слоя к слою вытекают из (0.3) только тогда, когда a ^k = a ^k+1.

В соответствии с условиями (0.3) температуры в точках контакта смежных слоёв отличаются на величины

T^k = T^k+1 - ( X ^k/ a ^k) д T^k/ д v ,

T^k+1 = T^k + ( X ^k+1 / a ^k+1) д T^k+1 / д v . (0.5)

Из равенства (0.5) следует, что непрерывность температур при переходе от слоя к слою обеспечивается только тогда, когда отношения ( X ^k/ a ^k) и ( X ^k+1/ a ^k+1) одновременно весьма малы. Очевидно, такая ситуация возможна, если коэффициенты теплопроводности X ^k+1 и X ^k и тепловые потоки д T^k/ д v и д T^k+1/ д v чрезвычайно низки. Наконец, такая ситуация может встретиться также при чрезвычайно больших значениях коэффициентов теплообмена, когда a ^k ^ ^ и a ^k+1 ^ ^ . При этом степень приближения a ^k и a ^k+1 к бесконечности должна быть одинаковой.

Ниже приведены результаты решения нестационарной задачи теплопроводности в цилиндрических телах слоистой структуры, в которых показаны существенные различия в характере распределения тепла при идеальном (0.1) и при неидеальном (0.3) теплообмене на границе контакта двух смежных слоёв.

• 1.    ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ В СЛОИСТОЙ СРЕДЕ

Ниже приведена постановка и решение задач нестационарной теплопроводности в цилиндрических телах слоистой структуры. Уравнения теплопроводности в k–ом слое цилиндрического тела [7, 8]

р ^kc _E ^k д T^k/ д t = д ( X ^k д T^k/ д r )/ д r +

+ ( X ^k/r ) д T^k/ д r + Q^k(r;t).        (1.1)

Здесь t – время, r – радиальная координата, р ^k- плотность, c _E ^k- удельная изобарическая теплоёмкость материала k–ого слоя, Q^k – внутренние источники тепла в нём.

Решения уравнений нестационарной теплопроводности (1.1) реализованы (см. [7]) в безразмерной системе координат ( ^ , т ) относительно безразмерной температуры 0 ^k

£ = (r-r¹)/R, т = t/t*,

0 ^k = (T^k(x,t) - T₀)/T*.          (1.2)

Здесь R– наружный радиус цилиндра, r1 – радиус внутренней поверхности первого слоя, t* и T* – характерные время и температура, T0 – начальное значение температуры.

В рамках поставленных здесь задач достаточно рассмотреть уравнения теплопроводности (1.1) с постоянными коэффициентами

0 k,t = ^1k 0k, ss +( ^1k/ ^) 0k, s + tok, (1.3) в которых введены обозначения цк = FokX k/ x*, Fok = X*t*/ (R)2 рk c E k, tok = Fok W kt*/ T* рk c E k (1.4)

Здесь X *- характерная теплопроводность, Fo^k – параметр Фурье материала k-ого слоя.

Уравнения теплопроводности (1.3) должны быть решены при начальных условиях

0 ^k ( ^ , 0) = 0.              (1.5)

и граничных условиях, заданных как на наружных поверхностях цилиндра, так и при переходе от слоя к слою. Граничные условия на наружных поверхностях принимаются в виде конвективного теплообмена

0 ¹,_x = - Bi 01 [ 0 - ф 01 ( т )], x = 0 (1.6.а) 0 K , x = - Bi LK [ 0 K - ф _L^M( T )] x = 1 (1.6.б) В проведенных ниже вычислениях принимается

	' А т	при	0 <  т <  т 1
ф 1( т )=	А т 1	при	t 1 <  т <  т 2 (1.7.а)
0	А( т 2 -	т ) при	t2 <  т <  т 3
	1 0	при	т 3 <  т

Ф _L^М( т )= 0                     (1.7.б)

В течение времени т 1 тепловое воздействие окружающей среды возрастает и в момент време- ни т = т 1 оно достигает максимальной величины А. В промежутке времени т 1 < т < т 2 тепловое воздействие является стационарным. Начиная с момента т = т 2, температура окружающей среды начинает снижаться. При т = т 3 она достигает начальной температуры окружающей среды и таким сохраняется до конца расчета.

Граничные условия (0.1) и (0.3) на контактных поверхностях записываются в различном виде при идеальном и неидеальном теплообмене. В случае идеального теплообмена для слоёв 2 <  k <  М

О ^k- 1 , _f = ( ^ _n^k / ^ _n ^k- 1 ) 0 ^k, _f ;

0 ^k- 1 = 0 ^k при £ = r^k/R.       (1.8)

При неидеальном теплообмене должны быть выполнены условия

0k, ^ = — BiLk (0k — 0k+1), при £ = rk/R 1 < k < М-1 (1.9.а)

0k+1, ^ = Bi0k+1 (0k+1 — 0k), при ^ = rk/R   1 < k< М-1 (1.9.6)

Параметры Био BiLk и Bi0 k+1 определяются из равенств

Bi L ^k = a ^k t*/ X ^k, Bi₀^k+1 = a ^k+11*/ X ^k+1. (1.10)

Поставленная задача (1.3)–(1.10) для уравнений параболического типа решается численно разработанным методом прямой и обратной прогонки [7, 9].

2.    РЕЗУЛЬТАТЫ РЕШЕНИЯ И ИХ ОБСУЖДЕНИЕ

Для решения задачи следует задаться исходными данными в соответствии с разработанной расчетной программой. Исходные данные, при которых были проведены начальные вычисления, приведены в табл. 1.

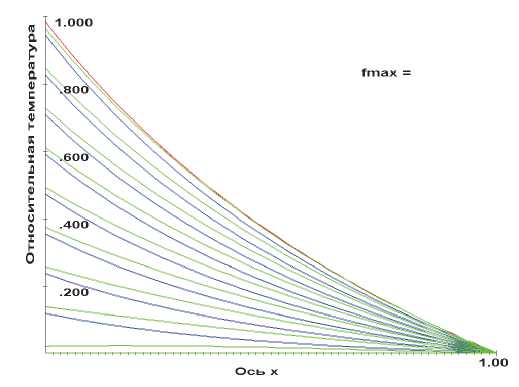
Вначале расчеты были проведены для однослойного цилиндра (120 <  r <  210). На рис. 1.а. приведено распределение относительной температуры по радиусу r для однослойного цилиндра. Температура отнесена к максимальному его значению (см. Аt в табл. 1).

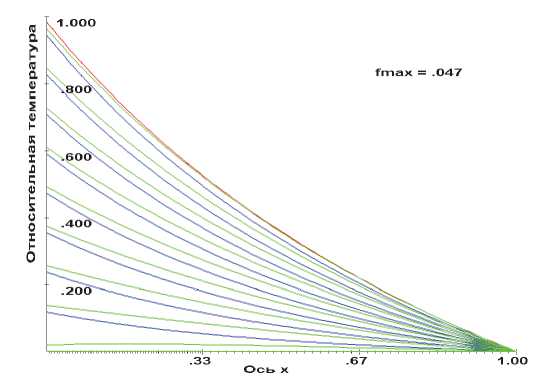
На втором этапе проведены исследования распределения температуры в трехслойном цилиндре при идеальном тепловом контакте (1.8) между слоями. Здесь сначала был проведен контрольный расчет, в котором предполагалось, что все слои цилиндра выполнены из одного материала с одинаковыми теплофизическими характеристиками. На рис. 1.б. приведены результаты специально выполненных вычислений. Сравнивая приведенные на рис. 1 а. и 1.б. результаты, можно видеть, что они идентичны, что и ожидалось при идеальном теплообмене между слоями из одного и того же материала. Проведенные сравнения свидетельствуют о достоверности полученных результатов и добротности разработанного алгоритма для расчета теплового состояния многослойной неоднородной среды.

Далее рассматривались слои с различными теплофизическими характеристиками в условиях идеального теплообмена между слоями. Рассмотренные варианты теплофизических характеристик приведены в табл. 2. В таблицах приведены лишь изменяемые параметры. Остальные параметры, использованные в вычислениях, заимствуются из табл. 1.

Таблица 1. Исходные данные

Параметры, размерность; обозначение	Слои, nlayer
	1	2	3
Система координат; ncoor	1	, цилиндрическая
Координаты начала х1(kх), конца х2(kх) слоя, мм;	120 150	150 180	180 210
Число отрезков в слое; NXL(kx)	20	20	20
	1	1	1
Общее время счета, сек; t i max	3600
Этапы температурного воздействия, сек; t1, t2, t3	900, 2250, 3150
Чи сло шагов по времени, nt	25000
Характерная температура, К; Tmax	2000
Начальная температура, К;	293
Максимальная температура, К; Аt	483
	1	1	1
Коэф фициенты тепло проводности, вт/ммК ;	0.1385	0.1385	0.1385
Удельная теплоёмкость, Дж/кг К; cvC(kx, nGtem)	406	406	406
Удельный вес, кг/мм3; dens(kx)	0.00000782	0.00000782	0.00000782
Коэф фициент те плообм ена в начале слоя , вт/мм2К; BiX0(kx, nGtem)	50.37	50.37	50.37
Коэф фициент те плообм ен а в конце слоя , Вт/мм2К; BiXL(kx, nGtem)	50.37	50.37	50.37

Таблица 2. Варианты теплофизических характеристик

Вариант	Параметры, размерность.	Слои
		1	2	3
1	Коэффициенты теплопроводности, вт/ммК	1.3850	0.1385	0.1385
2	Коэффици енты теплопроводности, вт/ммК	0.1385	1.3850	0.1385
3	Коэффици енты теплопроводности, вт/ммК	13.850	1.3850	0.1385

б

Рис. 1. Распределение температуры в цилиндрах (а – однослойный, б – трехслойный ) в различные моменты времени на этапе:

· роста температуры (синие линии, через 750 шагов по времени), выдержки температуры (красные линии, через 1000 шагов по времени), снижения температуры (зеленые линии, через 750 шагов по времени)

а

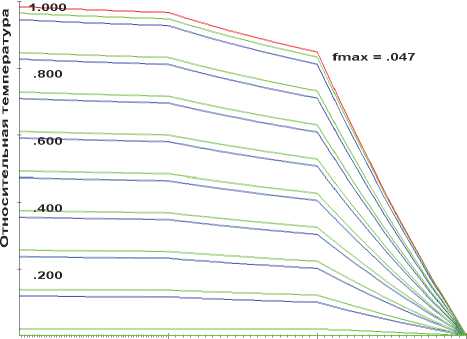
Результаты расчетов первых трех вариантов (см. рис. 2) свидетельствуют о качественном изменении характера распределения температуры в зависимости от значений коэффициентов теплопроводности в отдельных слоях. В соответствии с условиями (1.8) можно видеть, что при переходе от слоя к слою градиент поля температур меняется пропорционально отношению коэффициентов теплопроводности. При этом температура меняется непрерывно. Кроме того, рост коэффициента теплопроводности приводит к повышению равномерности распределения температуры в слое. Следует заметить, что при реализации решения методом конечных разностей и при переходе от слоя к слою условие (1.8) содержит не только отношение коэффициентов теплопроводности соседних слоёв, но и отношение длины ячеек Д ^к- 1 / Д ^к. При оценке реальной величины изменения тепловых потоков необходимо учитывать это обстоятельство. В нашем случае Д ^к- 1 = Д ^к и на рис. 2 изменения тепловых потоков при переходе от слоя к слою обусловлены только отношением коэффициентов теплопроводности ( Д 11 ^к/ Ц 11k ^-1) (к =2, 3).

Приведенные результаты свидетельствуют о возможности управления уровнями температур соответствующим выбором материала с требуемыми значениями коэффициентов теплопроводности.

Были проведены вычисления температурных полей при изменении теплоёмкости и удельного веса материалов. Влияние указанных параметров на распределение температуры в слоистом теле противоположно эффекту коэффициентов теплопроводности. При уменьшении величины произведения удельного веса и теплоёмкости тепло распространяется быстрее.

На третьем этапе расчетных исследований изучалось распределение температуры в трехслойном цилиндре при неидеальном тепловом контакте (1.9) между слоями. Если при идеальном контакте условия теплообмена зависят только от одного параметра – коэффициентов теплопроводности слоёв, то при неидеальном контакте два параметра – коэффициент теплопроводности и коэффициент теплообмена – определяют температурные условия на поверхностях контакта. Поэтому вначале исследовалось влияние коэффициентов теплообмена a на распределение температуры в трехслойном цилиндре. В этом случае теплофизические характеристики слоёв совпадали с начальными их значениями (см. табл. 1).

Из проведенных вычислений следует, что при одинаковом теплообмене между слоями а ^к 0 = a ^k L = 50.37 вт/мм²К распределение температуры в слоях не отличается от распределения температуры при идеальном теплообмене (см. рис. 1), что также видно из сравнения соотношений (0.4) и (0.2).

В проведенных исследованиях обнаружено,

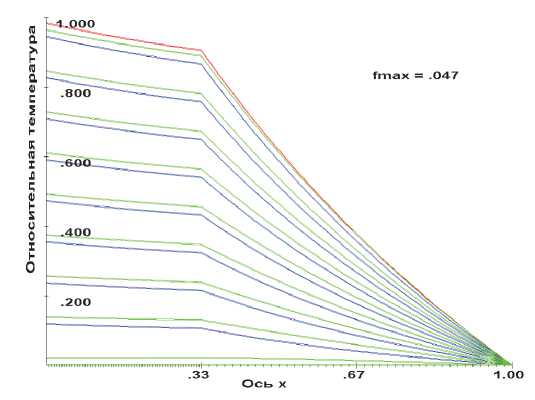
вариант 1.

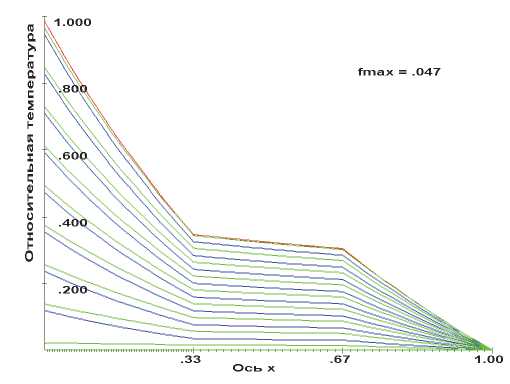
вариант 2

33 Ос х      67              100

Рис. 2. Распределение температуры в трехслойных цилиндрах в различные моменты времени на этапе:

• ·    роста температуры

(синие линии, через 750 шагов по времени),

• ·    выдержки температуры

  (красные линии, через 1000 шагов по времени), · снижения температуры

(зеленые линии, через 750 шагов по времени)

вариант 3.

Таблица 3. Комбинации коэффициентов теплообмена

Вариант Параметры, размерность Слои 1 2 3 4 Коэффициент теплообмена в начале слоя а0, вт/мм2К 50.37 50.37 0.05037 Коэффициент теплообмена в конце слоя aL, вт/мм2К 0.1504 0.05037 50.37 5 Коэффициент теплообмена в начале слояа0, вт/мм2К 50.37 50.37 0.05037 Коэффициент теплообмена в конце слоя aL, вт/мм2К 0.05037 0.05037 50.37 6 Коэффициенты теплопроводности, вт/ммК 0.001385 13.85 0.01385 Коэффициент теплообмена в начале слояа0, вт/мм2К 50.37 50.37 50.37 Коэффициент теплообмена в конце слоя aL, вт/мм2К 0.05037 0.5037 50.37 нице раздела 1-ого и 2-ого слоёв сильно меняется

что с уменьшением параметра a ^k L температурное поле в k-ом слое выравнивается, теплообмен с последующим слоем уменьшается – он, как бы, запрещается. Это заключение согласуется с соотношением (0.3).

В таблице 3 приведены комбинации коэффициентов теплообмена, результаты расчетов при которых обсуждаются ниже.

На рис. 3 приведены результаты вычислений по варианту 4. В первом слое распределение температуры в любой момент времени достаточно равномерное. Оно, в частности, обусловлено низким значением коэффициента теплообмена в конце первого слоя a 1L = 0.1504 вт/мм2К. На гра- градиент температуры, несмотря на то, что теплофизические характеристики материала слоёв одинаковы. Этот заметный излом в распределении температуры обусловлен отличием коэффициентов теплообмена a 1L и a 20.

На границе раздела 2-ого и 3-его слоёв можно видеть скачок, разрыв в значениях температур. Гладкость распределения температуры по обе стороны от точки разрыва одинакова. Это обусловлено не только одинаковыми значениями характеристик теплопроводности слоёв, но и равенством коэффициентов теплообмена a 2L = a 30.

В 5-ом варианте на границе раздела 1-ого и

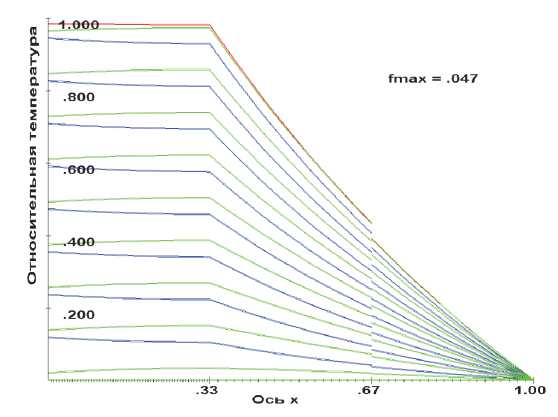
вариант 4

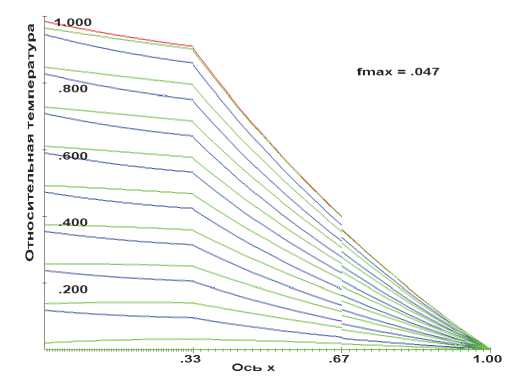
вариант 5

Рис. 3. Распределение температуры в трехслойных цилиндрах в различные моменты времени на этапе

· роста температуры (синие линии, через 750 шагов по времени),

· выдержки температуры (красные линии, через 1000 шагов по времени), · снижения температуры (зеленые линии, через 750 шагов по времени)

2-ого слоёв сильно меняется градиент температуры и заметен разрыв в значениях температуры (см. рис. 3).

Таким образом, расчетами подтверждена возможность разрыва в значениях температуры при переходе от слоя к слою при неидеальном тепло- обмене. Полученные и обсужденные здесь результаты обусловлены эффектом коэффициентов теплообмена на границе раздела слоёв.

Многочисленные вычисления, проведенные при различных значениях коэффициентов теплопроводности, показали следующее:

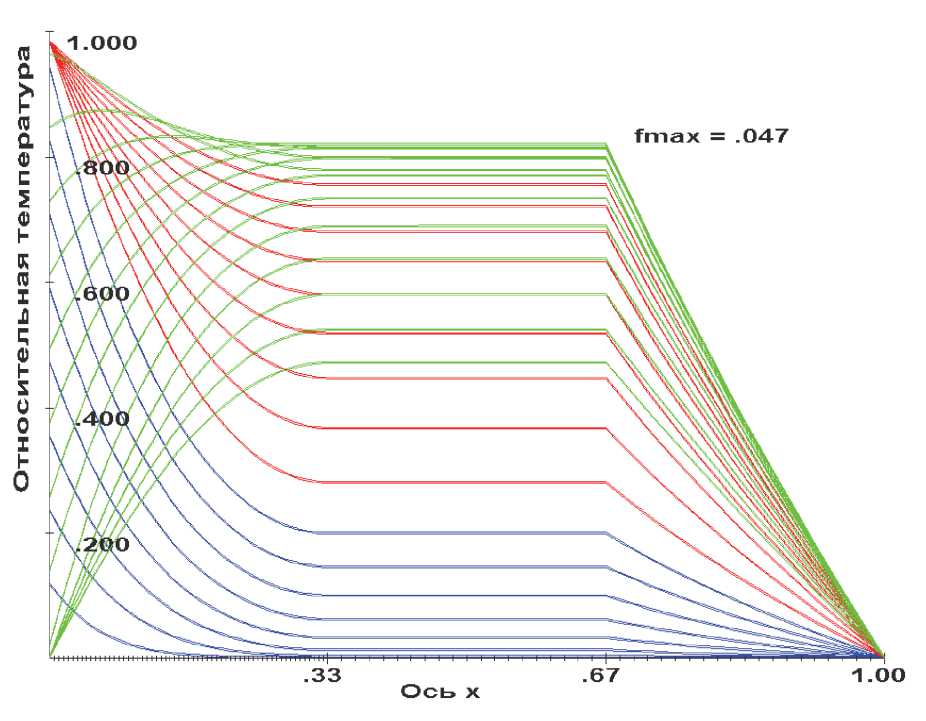
Рис. 4. Распределение температуры в трехслойном цилиндре (вариант 6) в различные моменты времени на этапе

· роста температуры (синие линии, через 750 шагов по времени),

· выдержки температуры (красные линии, через 1000 шагов по времени),

· снижения температуры (зеленые линии, через 750 шагов по времени)

• -    при малых значениях коэффициентов теплопроводности температура сильно уменьшается в слое,

• -    при больших значениях коэффициентов теплопроводности распределение температуры в слое становится более однородным и стационарный режим наступает быстрее,

• -    при переходе от слоя к слою сильно может меняться градиент температуры, разрыв в значениях температуры незначителен.

Приведенный на рис. 4 результат позволяет оценить совместное влияние, как коэффициента теплообмена, так и коэффициента теплопроводности на характер распределения температуры в слоях трехслойного цилиндра. Из-за малости коэффициента теплопроводности первого слоя наружная температура медленно внедряется в тело цилиндра. Из-за повышенного значения коэффициента теплопроводности второго слоя во втором слое быстро (мгновенно) достигается однородное (равномерное) поле температуры. Прогрев цилиндра интенсивно продолжается в моменты времени, когда на границе уровень температуры остается постоянным. Несмотря на то, что внутренняя поверхность цилиндра начинает охлаждаться из-за низкого значения коэффициента теплообмена температура продолжает перераспределяться во внутренних слоях (зеленые линии на рис. 4). Тем же обстоятельством объясняется тот факт, что цилиндр не успел охладиться в течение исследованного промежутка времени (nt =25000) t = 3600 сек.

Проведенные исследования позволяют утверждать, что выбором материала в слоистых конструкциях можно в широких пределах управлять характером распределения температуры в многослойных конструкциях.

Проведенные исследования позволяют решать уравнения параболического типа для неоднородных сред с более сложным характером изменения параметров среды. Результаты исследований позволили глубже понять влияние отдельных параметров на характер распределения температуры в отдельных слоях многослойной среды.