К сетевому представлению. Обучение

Пусть в некоторой нормальной системе выделен тернарный узел

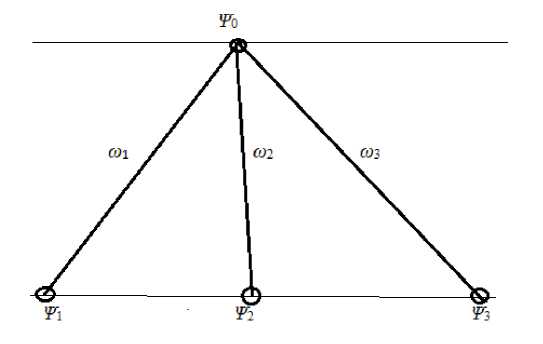
Рис. 1. Узел нормальной сети прямого распространения со смежными узлами нижестоящего среза.

(1) Для нормальной системы имеем соотношение

(2)              Wо = ш 1 ¥1 + ю 2 W2 + ш з Wз = nW, ieN = {1, 2,3}, при этом для коэффициентов выполняется условие

(3) Ю 1 + Ю 2 + ю 3 = ю\ = 1, а узлы системы определяются собственными функциями  Wi с собственными значениями равными единице

(4)    X i = xW i ,    x i = 1.

В общем случае для стоящего в иерархии узла на более высокой ступени в сети прямого распространения имеем зависимость от смежных узлов нижележащего среза

• (5)    x 0 = ω i xⁱΨ i = ω 1 x ¹ Ψ 1 + ω 2 x ² Ψ 2 + ω 3 x³Ψ 3 ,   i ϵ N.

Соотношение, аналогичное (1), справедливое для зависимости собственных функций, будет справедливо и для собственных значений

• (6)    x ⁰ = ω i xⁱ,      i ϵ N .

Элемент сети будем рассматривать как вектор

• (7)    x i = xⁱΨ i

и знаком (*) обозначать переход к сопряжённому вектору, опуская вниз у сопряжённого вектора индекс. Тогда, если ввести векторы

• (8)    x = ( xⁱ | i ϵ N ),      ω = ( ωⁱ | i ϵ N ),

равенство (4) можно записать в виде внутреннего произведения векторов

• (9)    x 0 = ω * x .

Рассмотрим две различные сети с одинаковой архитектурой. Выделим в них узел с собственной функцией Ψ 0 и рассмотрим его действие со смежными узлами. Поскольку архитектура сетей одинакова, то если узел одной сети имеет представление, изображённое на рис. 1, то аналогичное представление имеет и выделенный фрагмент второй сети, но описание их действия будет различными уравнениями – уравнением (8) и равенством

• (10)    y 0 = φ * y .

С учётом нормальности систем будем иметь

• (11)    y = x .

Таким образом, данные фрагменты будут отличаться только пропускной способностью связей. Будем полагать, что (8) и (9) состояния узла Ψ 0 из пространства X возможны состояний системы. Более того, считать состояние (9) целевым (плановым), а состояние (8) – фактическим. И полагать, что требуется последовательно сближать фактическое состояние с эталоном, естественно, с учётом ограничений на показатели функционирования.

Сравним данные фрагменты системы опираясь на основное метрическое тождество и используя свойства скобки процедуры Кэли-Диксона в алгебре Клиффорда в пространстве X ⨂ X в качестве элементов тензорного произведения c = x 0 y 0 . Для этого, на их бинарном соответствии z = ( x 0 , y 0 ), введём функции для внутреннего a = x 0 * y 0 и внешнего b = x 0 ∧ y 0 = i n b произведений, где n единичный вектор в представлении x 0 × y 0 = b n и гомоморфизм в пространстве определим функционалом D = c ² = D ( z ). Получаем, что на данном бинарном соответствии справедливо тождество Пифагора

• (12)    a ² + b ² = c ²,

а для его тензорной кватерниональной формы имеет место волновое представление

• (13)    c = cΨ ,     Ψ= exp (i n θ ),

Будем полагать, что фактическое состояние системы есть образ (модель) оригинала, т.е. его расчётного состояния - эталон, в практической деятельности естественно последовательное стремление фактического состояния к эталону, и считать, что, не нарушая общности, ограничения (накладываемые на производственные факторы)    для подобного совершенствования отсутствуют. Как скульптор из глыбы мрамора высекает Аполлона, так и мы будем последовательно совершенствовать образ, последовательно отсекая мешающие обстоятельства в нашем совершенствовании. Для производственной системы это модернизация производства, стимулирование и обучение персонала и т. п.

Как правило, если рассматривать производственные сети, то это будут многоуровневые иерархические структуры и алгоритм их совершенствования, с учётом сети прямого распространения, можно строить поэлементно, либо послойно, например, снизу вверх, либо сверху вниз. Из статистического сходства соответствующих слоёв вытекает основа алгоритма - последовательное улучшение корреляционного сходства.

Коэффициент корреляции определяется формулой

• (14)    r = a/c .

Применяя неравенства Коши-Буняковского

• (15)    a <= c ,

в котором равенство достигается при полном соответствии сравниваемых слоёв, и полагая r> 0,находим

• (16)    a = rc <= c .

При монотонном росте коэффициента корреляции образ будет последовательно стремиться к эталону. Предположим, что при темпах прироста T ( x ) некоторого фактора сети темпы прироста коэффициента корреляции равны T ( r ). При условии, что эластичность (чувствительность) коэффициента корреляции относительно данного изменения равна s получаем

• (17)    r ( t + 1) = (1 + sT ( x )) r ( t ).

Заключаем, что корреляция будет возрастать, если показатели s и T ( x ) будут одного знака.

Пусть x и у произвольные фрагменты исходных систем, находящихся в структурном бинарном соответствии, а x и у - некоторые соответствующие их узлы. Для эластичности коэффициента корреляции данных фрагментов по показателю x получаем выражение

• (18)    s = xy / a ( x , y ) - x 2 / c ²( x , y ),

т.е. сумма S = ^s эластичностей коэффициентов корреляции (17) по всем узлам данных фрагментов равна нулю. Следовательно, среди показателей эластичности узлов есть как положительные, так и отрицательные. Сумму положительных слагаемых обозначим S⁺ , а сумму абсолютных величин отрицательных слагаемых обозначим S^- . Приходим к выражению

• (18)                S = S + - S = 0.

Представление (18) такого расслоения показывает, что качественное сближение модели с эталоном можно проводить двумя методами улучшая качество модели за счёт совершенствования узлов:

• a)    обращая внимание только на показатели с положительными коэффициентами эластичности, т.е. случай 1);

• b)    обращая внимание только на элементы сети с отрицательными коэффициентами эластичности, случай 2);

• c)    применяя в сближении одновременно как случай 1), так и случай 2).

Это свидетельствует, что "скульптор" из одной и той же " мраморной глыбы" может получить множество количественно различных, но качественно подобных моделей, т.е. в представлении (12) у таких моделей могут быть близкими по значению аргументы θ , но сильно варьироваться количественные показатели – амплитуды σ , т.е. x = k y , σ ( x ) = kσ ( y ).

На примере ненормированного фрагмента сети рис.1 определим состояния x = (1; 2; 3) и y = (1; 1; 2). При одинаковом качестве состояний их компоненты пропорциональны. Предъявляя y как эталон, состояние x можно привести к качественно подобному y состоянию двумя методами: 1) уменьшением компонент x ² и x ³, и 2)увеличением в два раза компоненты x ¹ и увеличением в полтора раза компоненты x ³. Если в первом случае получаем x = y , то в случае 2) имеем x = 2 y . Это объясняют и значения коэффициентов эластичности: s 1 = 5/126, s 2 = - 8/126, s 3 = 3/126.

Отметим, что волновое представление (12) даёт возможность наблюдать процесс обучение в цветовой гамме.

"Экономика и социум" №2(69) 2020