К статье Н.В. Кравцова и В.В. Рагульского “Использование кольцевого лазера для исследования изотропии пространства”

Показано, что ожидаемый сдвиг частот встречных волн в предлагаемом Н.В. Кравцовым и В.В. Рагульским эксперименте с использованием кольцевого лазера, в одном из плеч которого находится конденсированная среда с отличным от единицы показателем преломления, и предназначенным по замыслу авторов для поиска возможной пространственной анизотропии скорости света, равен нулю, даже при наличии возможной анизотропии скорости света.

В ноябрьском номере “КЭ” за 2000 год была опубликована статья Н.В. Кравцова и В.В. Рагульского [1]: “Использование кольцевого лазера для исследования изотропии пространства”, в которой предлагался эксперимент, позволяющий с высокой точностью (до 10 ^{- 21} т 10 - 22 ) проверить эйнштейновский постулат о независимости скорости света от направления в пространстве, и, тем самым, подтвердить справедливость СТО.

Основой схемы предлагаемого эксперимента является кольцевой лазер с резонатором в виде “восьмерки” (для исключения влияния эффекта Саньяка на частоты генерируемых волн), часть резонатора которого заполнена прозрачной конденсированной средой с отличным от единицы показателем преломления n .

По замыслу авторов, время обхода световой волной резонатора, в одном из плеч которого находится конденсированная среда с отличным от единицы показателем преломления n , при наличии возможной пространственной анизотропии скорости света A c должно зависеть от ориентации резонатора в пространстве. В результате должна возникнуть разность времен распространения встречных волн A t , равная по оценкам авторов:

2 ( n - 1 ) l A c l A n

A t = ~--^---,                        (1)

c2          c которая в работающем кольцевом лазере должна приводить к возникновению сдвига частот встречных волн ∆ω на величину:

∆ω =2(n-1) ω

l ∆ c l ∆ n

-

Lc L

где c – это усредненная по двум встречным направлениям скорость света; ∆ c – возможное отличие “однонаправленной” скорости света от средней; n – усредненный по встречным направлениям показатель преломления конденсированной среды, находящейся в резонаторе; l – длина этой среды; ∆ n – возможная разность показателей преломления конденсированной среды для встречных волн; L - оптическая длина лазерного резонатора.

По мнению авторов, из формулы (2) на основании независимых измерений ∆ n и ∆ω можно найти величину возможного отклонения односторонней скорости света ∆ c от средней.

Как известно, ранее, один из авторов (В.В. Рагульский) в работе [2] основываясь на собственных результатах измерения ∆ω по аналогичной схеме, однако, без использования кольцевого лазера, и пользуясь данными измерений ∆ n из своей предыдущей работы [3], где было установлено, что преломляющее действие конденсированной среды на световые волны с точностью ~ 5 ⋅ 10 ^{- 8}

не зависит от ее ориентации в пространстве, утверждал, что в лабораторных условиях фазовая скорость света не зависит от направления. А потому постулат Эйнштейна о пространственной независимости скорости света от направления можно считать доказанным в пределах данной точности эксперимента, хотя на самом деле точность измерения сдвига частот встречных волн ∆ω в эксперименте [2] (в эксперименте измерялось смещение интерференционных полос) составляла всего лишь около 4.3 ⋅ 10 ^{- 4} (но не ~ 5 ⋅ 10 ^{- 8} ) и оставляла желать лучшего.

В действительности же, однако, величина ∆n , измеренная в эксперименте [3], т.е. определяемая как разность отношений синусов углов падающего и преломленного лучей в противоположных направлениях, и величина ∆n в формулах (1) и (2), определяемая как разность отношений скоростей падающего и “преломленного” лучей (“преломленный” луч в данном случае распространяется в том же направлении, что и падающий, поэтому взят в кавычки) в противоположных направлениях, это две разные величины и имеют разный физический смысл. Поэтому равенство нулю сдвига частот ∆ω в эксперименте [2] и равенство нулю ∆n в эксперименте [3] не означает, что равно нулю и ∆c в формулах (1) и (2). Разность ∆c может быть при этом любой, так как в действительности величина ∆n применительно именно к этой ситуации, т.е. определяемая как разность отношений скоростей падающего и “преломленного” лучей в противоположных направлениях, неизвестна.

Закон преломления Снеллиуса n = sin α/sin β                                             (3)

применительно к ситуации [3], где α - угол падения, β - угол преломления, n – показатель преломления среды (поэтому он и называется показателем преломления) выполняется всегда, независимо от скорости света, что легко доказать.

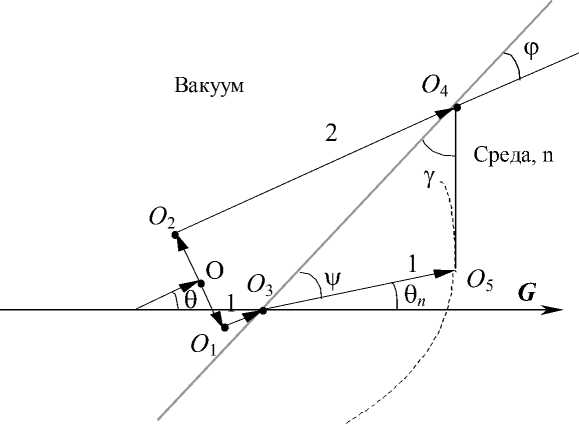
Рис. 1. К выводу закона преломления света в случае анизотропного пространства

Действительно, пусть скорость света в вакууме равна:

c(θ) =     c ,

1+βcosθ где θ - это угол между осью анизотропии пространства и направлением распространения света, а β - это параметр (не путать с углом преломления β в формуле (3)), характеризует теперь степень анизотропии пространства. Скорость света в среде с показателем преломления n будет равна в этом случае (см., например, [4]):

cn (6n ) =

c n + P cos 6n ’

где 6n - это угол между осью анизотропии пространства и направлением распространения света в среде.

Пусть тонкий когерентный пучок света распространяется под углом 6 к предполагаемой оси анизотропии (рис. 1). В точке O пучок расширяется (в перпендикулярном направлении) до ширины O 1 O 2 = 2 h и падает на плоскую границу раздела O 3 O ₄ двух сред (вакуум-среда), ориентированную под углом ф к направлению распространения падающих фотонов, и преломляется. Под каким углом 6 _n к оси анизотропии пространства (в данном случае под углом ф к поверхности раздела сред) преломится пучок в среде?

Согласно гипотезе Гюйгенса-Френеля границу раздела вакуум-среда можно рассматривать как источник вторичных элементарных волн. Скорость вторичных волн в среде определяется формулой (5) (здесь: ф + 6 —180° <6n < ф + 6). Направление распространения огибающей (линии O4 O5 ) вторичных волн (в нашем случае, это угол 6n или, если рассматривать по отношению к поверхности раздела сред, угол ф), даст нам направление распространения преломленного пучка в среде.

Лучи 1 и 2 в точке O расширяются согласно (4) со скоростью

Си .=cг = c ,                    (6) 11,2   1 + в cos(9 — / + 90°)   1 ± в sin 9 где индекс ” 11 ”- соответствует лучу 1, распространяющемуся перпендикулярно вниз под углом 6ц = 6 — 90° к оси анизотропии пространства, а индекс ” 1 2 ”- соответствует лучу 2, распространяющемуся перпендикулярно вверх под углом 612 =6 + 90°.

Для времени распространения лучей 1 и 2 из точки O в точки

O ₃ и O ₄ , соответственно, имеем

OO. OO     GO, OO OO cosф 1   13         2   13   34 t 1      c 1 1    '    c ( 6 ) ,    t 2       c 1 2    '    c ( 6 )   '        c ( 6 )       '           (7)

Разность времен распространения лучей, очевидно, равна

OO2 O3O cos ф OO, A t = t 2 — tv =     2 + 3 4       —     1 .                       (8) 2 ' c 1 2         c ( 6 )        c 1 1

Так как   ОО1 = ОО 2 = h, О3 О4 = 2 h /sin ф, разность   At перепишется:

A t =

2h cos ф + Р cos(0 + ф)

c sin ф

Радиус вторичной волны (O3 O5 ) луча 1 в среде в момент времени t2 , очевидно, равен

Оз O5 = Cn (9 n )A t =

2 h    cos ф + P cos(0 + ф)

n + P cos 9 _n

Sin ф

,

радиус вторичной волны луча 2 равен нулю. Нужно найти в образованном треугольнике О 3 О 4 О 5 угол ф , соответствующий максимуму угла у ?

Для углов ф и Y в треугольнике О3 О4 О5 справедлива теорема косинусов:

/( О 3 О 5 ) ² =( О 4 О 5 ) ² +( О з О 4 ) ² - 2 ( О 4 О 5 )( О з О 4 ) cos Y ,     ₍₁₁₎

!( О 4 О 5 ) ² =( О 3 О 5 ) ² +( О 3 О 4 ) ² - 2 ( О з О 5 )( О з О 4 ) cos ф .

Решая систему (11) относительно Y и произведя замену ф = 0 + ф — 0 n , получаем функцию угла Y :

1    cosф + pcos ( 0 + ф )

—

Y = arccos-

sin ф   sin ф ( n + р cos0 _n )

cos ( 0 + ф —0 _n )

1 V sin ф J

^^^^^в

2cosф + pcos(0 + ф)   (0+   0 ) + | cosф + Pcos(0 + ф) । sin2 ф(n + Pcos0n)            n ( sinф(n + Pcos0n) J

Численные расчеты показывают, что максимум угла Y достигается при угле 0n , точно удовлетворяющий соотношению:

n cos(0 + ф — 0n) = cos ф, где 0 + ф — 0n = ф, откуда следует закон преломления Снеллиуса (3).

А вот само отношение скоростей падающего и “преломленного” лучей может быть разным в разных направлениях. В нашем случае, как следует из формул (4) и (5), оно равно

c (0) / cn (0 „ ) =

n + Р cos 0 n 1+ Р cos 0

(здесь 0 = 0 _n ), откуда для A n применительно к ситуации [1, 2]

получаем:

An =

2р(1 — n)

1 — Р ²

а не A n = 0 . Поэтому равенство нулю сдвига частот Ato в экспериментах [1] и [2], и равенство нулю A n в эксперименте [3] вовсе не означает, что равно нулю и A c .

Чтобы определить A n применительно к ситуации [1, 2] надо ставить эксперименты в схожих условиях. Во-первых, чтобы падающий и “преломленный” лучи имели одинаковое направление, как и в экспериментах [1, 2]. Во-вторых, необходимо измерять именно отношение скоростей падающего и “преломленного” лучей, а не коэффициент преломления n , как в ситуации [3], который, как мы видели, всегда сохраняется, даже когда скорость света анизотропна. И когда авторы [1] совершенно необоснованным образом утверждают, что в работе [3] экспериментально установлено, что преломляющее действие конденсированной среды на световые волны с точностью ~5 • 10 - 8 не зависит от ее ориентации в пространстве и, тем самым, в формулах (1) и (2) величина A n также автоматически определена, то это является недопустимым переносом результатов опыта [3] на область, выходящую за пределы их применимости. Нельзя переносить результаты экспериментов [3] на несовместимые с ними эксперименты [1,2]. Это разные эксперименты. Результаты экспериментов [3] лишь показывают, что работает именно формула Снеллиуса (3) и не более.

Далее, раз идет речь о таком фундаментальном высокоточном эксперименте, как [1], то и расчет ожидаемой величины сдвига частот встречных волн должен быть выполнен подобающим образом на очень высоком уровне и не должен содержать никаких произвольных и необоснованных предположений, противоречащих известным экспериментальным фактам.

Теоретическая модель скорости света

С1 2 = c — / + Ac,(15)

использованная авторами [1-3] для расчета ожидаемого сдвига частот Ato , противоречит известным экспериментальным фактам.

1         12

Величина--1--=-----—— ^ —, получающаяся в этом c + A c c — Ac c2 —(Ac fc случае, не согласовывается с экспериментами типа Майкельсона-Морли. Ни одна теоретическая модель не должна противоречить известным экспериментальным фактам. Точность экспериментов аналогичных Майкельсона-Морли, доведенная в настоящее время до 1.7 • 10—15 (см., например, [5,6]), не подтверждает модель (15).

Чтобы модель скорости света находилась в соответствии с экспериментами типа Майкельсона-Морли, она должна быть равной, либо c ( 0 ) ~ c (это самый примитивный вариант, какой постулируется в СТО), либо (4), неважно, чем бы ни была вызвана эта анизотропия, необязательно связанная с движением Земли. В последнем случае, как и в СТО, световой волне, распространяющейся, например, в прямом и обратном направлениях на отрезке длины l , расположенном под произвольным углом 0 к предполагаемой оси анизотропии, потребуется время t :

t = -(1 + в cos 0 ) + — ( 1 + в cos ( 0 +180° )) = —,           (17)

cc    c не зависящее от направления ориентации 0 отрезка l в пространстве. Поэтому в этом смысле эксперименты [5, 6] обречены на неудачу.

Таким образом, вновь возвращаясь к нашей теме об ожидаемом сдвига частот Ato встречных волн в эксперименте [1], световой волне на полный обход трасс сначала в одном направлении, когда световая волна распространяется в вакууме по трассе длины l под углом 0 к предполагаемой оси анизотропии пространства, а затем в обратном направлении под углом 0 +180° по трассе такой же длины l , но заполненной прозрачной конденсированной средой с отличным от единицы показателем преломления n , а затем вся эта процедура вновь повторяется в обратном порядке согласно (4) и (5) при наличии пространственной анизотропии скорости света потребуется время t1 = —(1 + в cos 0) + —( n + в cos(0 +180°)).                  (18)

cc

На такой же пробег по обратному маршруту потребуется время t2 = —(n + в cos 0) + — (1 + в cos(0 +180°)).                 (19)

cc

Таким образом, разность времен A t обхода световых волн в противоположных направлениях применительно к ситуации [1], даже при наличии анизотропии скорости света равна:

A t = t 1 - t 2 = 0 ,                                                (20)

а не (1), как утверждают авторы [1].

Таким образом, предлагаемый эксперимент [1], а также уже выполненный эксперимент [2] (а также эксперименты типа [5, 6]), в которых используется замкнутая траектория света, не может в действительности, ни    опровергнуть, ни подтвердить эйнштейновский постулат о независимости скорости света от направления, а равно и такую зависимость, и к анизотропии скорости света не чувствителен.

Скорость света при этом может быть, как изотропной, так и анизотропной, но все равно эксперимент отличить одно от другого не сможет. В свое время Майкельсоном, по-видимому, был уже введен запрет на такого рода научных проектов, в которых используется замкнутая траектория света. Конечно, я не против постановки эксперимента [1], даже при отрицательном исходе, любой эксперимент сам по себе уже ценен. Я против той трактовки результатов экспериментов, что навязывают авторы [1].