К теории автомобильных потоков

Дорожные сети мегаполисов все более насыщаются автомобилями. Следствием этого на магистралях наблюдаются протяженные очереди, а на перекрёстках спонтанно возникают скопления блокирующих друг друга автомобилей. Эти недостаточно изученные к настоящему времени явления все более тормозят потоки автомобилей и тем самым создают все более осязаемые проблемы — социальные, экологические и экономические.

Миграцию очередей в реальном времени на московской дорожной сети можно наблюдать на интернет-сайте «Карты дорожных пробок на Яндексе». Сайт экспонирует карту дорог г. Москва, на которую с интервалом 4--5 минут наносятся изменения в распределении дорожных «пробок».

Рассмотрим отрезок магистрали между перекрёстками. При красном сигнале светофора, установленном на выезде из магистрали в перекрёсток, поток автомобилей тормозится с образованием очереди из останавливающихся автомобилей. С включением зеленого сигнала головной автомобиль начинает движение, а следующий за ним становится головным. Если в некоторый момент времени тело очереди не пусто, то в этот момент к очереди может присоединиться следующий автомобиль, который становится хвостовым. Такую очередь из стоящих автомобилей назовем пробкой. Ее голова и хвост перемещаются по магистрали в направлении, противоположном движению.

Существуют два случая:

• —    пробка рассеивается за конечное время на достаточно длинном отрезке магистрали, когда интенсивность потока, входящего в тело пробки, меньше интенсивности отделения головных автомобилей;

• —    длина пробки не убывает с течением времени, когда интенсивность входящего потока больше или равна интенсивности выходящего потока из тела пробки.

Как в первом случае (при определённых отношениях длины отрезка магистрали и длительности красного сигнала), так и всегда во втором случае пробка за конечное время достигает соседнего перекрёстка и может тормозить на нём потоки с других магистралей.

Полное или частичное покрытие площади перекрёстка телами пробок, при котором отсутствует возможность отделения головных автомобилей от тел пробок, назовем затором.

Рассмотренный механизм образования заторов может приводить как к полному или частичному рассеиванию автомобилей на исходящих от перекрёстка магистралях, так и к росту длин пробок на входящих магистралях с захватом заторами соседних перекрёстков.

Отметим двойственную роль пробок на дорожной сети. С одной стороны, образование пробок является необходимым технологическим следствием светофорного регулирования. С другой стороны, первичная пробка индуцирует эффект затора, который в свою очередь приводит к неконтролируемому росту длин вторичных пробок, поражающих дорожную сеть.

Одной из целей построения модели и теории дискретного потока является установление условий, при которых первичная пробка успевает рассеяться в пределах магистрали, не достигнув соседнего перекрёстка. В этом контексте модель однорядного дискретного потока является первичным объектом для исследования.

В общем контексте модель дискретного потока частиц, которая сформулирована ранее в работах [2--4] и развитая в данной работе, ближе всего примыкает к модели В.А. Марченко [5], в которой цепочки частиц укладываются в систему каналов со структурой графа.

Принципиальное отличие моделей состоит в следующем. Модель В.А. Марченко предусматривает упругое взаимодействие соседних частиц. А модель данной работы предусматривает взаимодействие соседних частиц в соответствии с законом безопасной дистанции. Ещё раз подчеркнем, что этот закон основан на известных экспериментальных данных о зависимости дистанции между частицами от их скорости.

Другие представления о моделях потока автомобилей на магистральных отрезках дорог можно получить из работ [6--8]. Их более полный обзор содержится в [9].

Также заметим, что в исследованиях [1], по-видимому, впервые, проблема организации дорожного движения в крупных городах была сформулирована как системная, с попыткой создания сетевой концепции светофорного регулирования потоков автомобилей. Комбинаторный анализ различных схем расщепления потоков на регулируемом перекрёстке представлен в [10].

Данная работа, содержащая вывод ДФ-урав-нений и их интегрирование, является первой частью теории дискретного потока. Вторая часть этой теории — динамика очереди — будет представлена в следующих номерах журнала.

• I . Модель дискретного потока

Схема дискретного потока. Рассмотрим однорядную полосу для движения автомобилей, с которой свяжем координатную ось S (рис. 1). Полоса наполнена движущимися друг за другом автомобилями, образующими то, что будем называть дискретным потоком. Относительно этого потока предположим следующее:

• —    автомобили представляются точечными частицами;

• —    запрещены въезды и выезды автомобилей через боковые ограничивающие линии;

• —    скорость каждого автомобиля в произвольный момент времени направлена по координатной оси или равна нулю;

• —    взаимодействие соседних частиц в потоке подчиняется закону безопасной дистанции.

0 ф        ф 0   0 ф 0   0     0

S+ shi s«         S" S

Рис. 1. Однорядный дискретный поток частиц. S ⁺ , s i , S ^- ∈ S

Изложим содержание закона безопасной дистанции.

Предварительно заметим, что начало исследований механизмов взаимодействия автомобилей в потоке относится к 30-м годам прошлого века (см. [1]). В этот период было экспериментально установлено, что максимальная интенсивность потока автомобилей в однорядной полосе составляет величину 2000 авт / ч, которая достигается на скоростях 40--50 км / ч. Ясно, что величина 2000 авт / ч определяет пропускную способность однорядной полосы.

Закон безопасной дистанции. В рассматриваемом потоке частиц обозначим через s i ( t ) координату i -й частицы (автомобиля) в момент времени t , s i ( t ) E S , t E R , i E N . Дистанцию между соседними частицами с номерами i и i + 1 обозначим через Л i +i ( t ) = s i ( t ) — s i +i ( t ), i E N и свяжем её со скоростями частиц. С этой целью рассмотрим стационарный однородный поток, в котором

• —    равны и постоянны скорости всех частиц: s i ( t ) = s i +1 ( t ) = v = const, t E R , i E N ;

• —    равны и постоянны дистанции между соседними частицами: Л i ( t ) = Л = const, t E R , i ^ 2.

В плоскости R x S такому потоку соответствует семейство параллельных прямых с равными дистанциями (рис. 2). Очевидны формулы

Л v = лt. q = v^, где ц = -^, q = 217; здесь Л — дистанция между соседними частицами, Лt — интервал времени, в течение которого частица проходит дистанцию Л со скоростью v, μ — плотность частиц, q — интенсивность движения частиц.

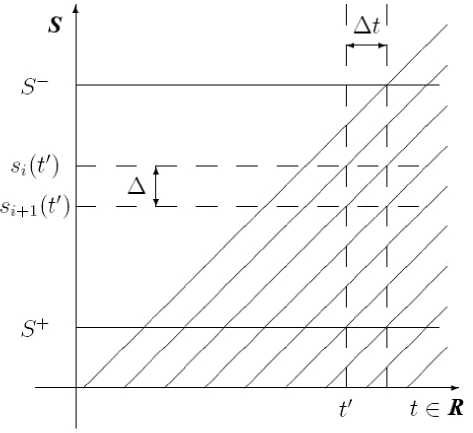
Рис. 2. Графики движения частиц, образующих однородный стационарный дискретный поток

Дистанция Л при прочих равных условиях является функцией скорости v . Эта зависимость в основном определяется двумя факторами — длиной тормозного пути и запаздыванием реакции водителя при изменении скорости впереди движущегося автомобиля.

На рис. 3 представлены графики описанных выше следующих функций: ф ( v ), ц ( v ), Л t ( v ) и q ⁽ v ).

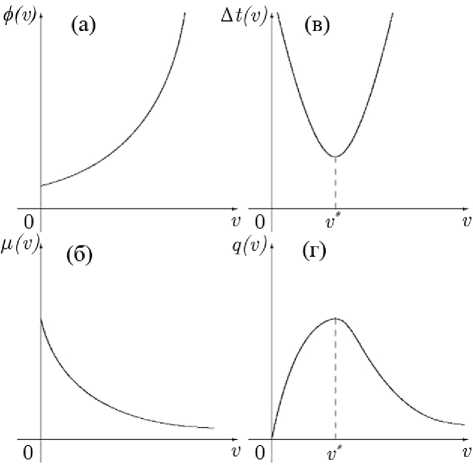
Рис. 3. Графики функций: а — функция безопасной дистанции ^ ( v ), б — плотность потока ^ ( v ), в — функция временного интервала △ t ( v ) иг — интенсивность потока q ( v )

В каждой паре соседних частиц из однорядной полосы выделяем лидера и преследователя, относительно которых считаем, что

• —    преследователь в каждый момент времени имеет возможность сохранять свою скорость либо переключаться на скорость лидера, то есть: s i +1 ( t ) G V i +1 ( t ), V i +1 ( t ) = { s i +1 ( t - ) ,s i ( t ) } i G N , где s i — скорость лидера с номером i, s i । — скорость преследователя;

• —    преследователь, имея выбор из двух скоростей, стремится поддерживать безопасную дистанцию, следуя правилам:

• (а)    если Л i +1 ( t ) > ^ ( s i ( t )), то преследователь стремится сократить дистанцию Л i +1 , выбирая максимальную скорость s i +1 ( t ) = max V i +1 ( t ),

• (б)    если Л i +1 ( t ) < ^ ( s i ( t )), то преследователь стремится увеличить дистанцию Л i +1 , выбирая минимальную скорость s i +1 ( t ) = min V i +1 ( t ),

• (в)    если выполняется равенство Л i +1 ( t ) = ^ ( s i ( t )), то преследователь для поддержания безопасной дистанции должен двигаться со скоростью лидера, то есть s i ( t ) = s i ₊₁ ( t );

• —    действия каждого лидера не зависят от действий преследователя;

• —    движение лидера с номером i = 1 считается заданным, например, указателями скорости, размещенными по длине полосы; в этом случае движению лидера с номером i = 1 может быть сопоставлено обыкновенное дифференциальное уравнение первого порядка c кусочно-постоянной правой частью. При этом скачки сопоставляются точкам полосы, где установлены указатели скорости.

Дифференциально-функциональные уравнения (ДФ-уравнения) однорядного дискретного потока. Учитывая изложенное, уравнения дискретного потока с безопасной дистанцией представимы в следующем виде:

S1 = f ⁽ s 1 ) , s 1 ^G S,                ⁽¹⁾

{max Vi +1( t),      Л i+1( t) > ^ (si (t)), s i (t),                Л i+1( t ) = ^ (si (t)), min Vi +1(t),       Лi+1(t) < ^ (si (t)).

Здесь введены следующие обозначения: f (s 1) — кусочно-постоянная функция со скачками в точ- ках полосы, где установлены указатели скорости; Vi +1(t) = {si+1(t—),si(t)}; Лi +1(t) = si(t) - si+1 (t), t G R, i G N; ^(si (t)) — заданная неубывающая функция от скорости лидера — представление закона безопасной дистанции; si (t) — координата i-й частицы в однорядной полосе, si(t) — её скорость, si(t) G S, t G R, i G N.

Краевые условия. К уравнениям дискретного потока (1), (2) следует присоединить начальные и граничные условия. Запишем общее представление этих условий.

Начальные условия для уравнений (2) в начальный момент времени задаются распределением частиц в полосе, а также начальным распределением их скоростей; то есть в момент времени t = t о задаются следующие два множества:

{ s i ( t о ) } , { s i ( t о - ) } ,

si (tо) > si+1 (tо) G [S + ,S-), is i (t о -) > 0,

где i G 2 ,I о и I о — число частиц в отрезке полосы [ S ⁺ ,S ^- ) в момент времени t о , I о G N , I о <  + го , а S ⁺ , S ^- — граничные точки этого отрезка.

Для интегрирования уравнения (1), как для обыкновенного дифференциального уравнения, в начальный момент времени t = t о достаточно задать положение первой частицы в полосе s 1 ( t о ) G [ S ⁺ ,S ^- ).

Граничное условие в сечении S ⁺ задается моментами времени проезда с ненулевой скоростью сечения S ⁺ i -ми частицами, i = 1 ,I ⁺ ; то есть считаются заданными следующие множества:

{ t + } ,t i ⁺ < t ++1 ,

{ s i ( t + ) } , ^i i ( t + ) >  0 .

Ясно, что при этом следует считать si (ti+) = S+, i = 1 ,I+, I+ < + го.

Здесь I ⁺ — общее число частиц, вошедших в отрезок полосы [ S ⁺ ,S ^- ) за время [ t о , + го ). Отметим, что множества из (4) считаются конечными.

Граничное условие в сечении S ^- задается аналогично граничному условию в сечении S ⁺ следующими множествами:

^{t i ^},t i < t i +1 ,

{ s i ( t - _ )} ,s i ( t -- ) >  0

при условии si(ti ) = S , i = 1 ,I , I < + го.

Здесь I - — общее число частиц, вышедших из отрезка полосы [ S ⁺ ,S - ) за время [ t о , + го ). Также отмечаем, что множества (5) считаются конечными. Особенности других представлений краевых условий (5) излагаются далее.

• II.    Интегрирование уравнений потока частиц

Программное движение лидера. Пусть в соответствии с п. I движению лидера сопоставлено обыкновенное дифференциальное уравнение с кусочно-постоянной и неотрицательной правой частью следующего вида:

s = f (s),s G [S+ ,S-) C S, f (s) = vn,s G [S(n- 1,S(n)) C [S + ,S —), n = 1 ,n + 1, где n — число скачков в интервале [S+ ,S-), n < + ro,S(n) — координаты точек скачков скорости, vn — значение скорости лидера (i = 1) на интервале [S(n- 1),S(п)). При этом S(0) = S+ и S(п+1) = S-,S+ ,S- < + го.

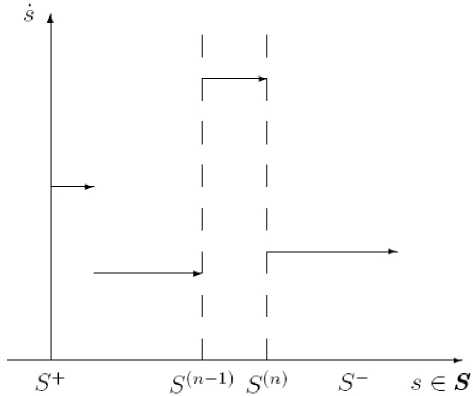
Рис. 4. Скоростная программа движения лидера в однорядной полосе

Обозначим через s (t) решение уравнения на интервале [t' ,t''), t" < + го при начальных данных s i( t') = S +.

Считая функцию f ( s ) непрерывной справа, решение s 1 ( t ) строим в классе кусочно-линейных неубывающих функций. Решение представимо следующим интегралом:

^f S ⁺ + v 1 ( t - t ' ) ,t G [ t ' ,n i ) ,

• ^s 1 ⁽ t ) =    S ^{+ +} £ m =1 v m А П т ⁺ v n ( t ) ⁽ t ^- П п ( t ) ) ,

• I    t G [ n 1 ,t '' ) ,

Пп = Пп-1 + А Пп, n+1

t '' = П п = t ' + ^ А П т ,          (6)

m =1

n ( t ) = max { n : п _п ^ t } , где n — число скачков функции f ( s ) на интервале [ S ⁺ ,S ^- ), s G [ S ⁺ ,S ^- ).

График функции f ( s ) представлен на рис. 4. Подчеркнем, что здесь все v _n > 0.

Заметим, что если формально снять ограничение, связанное с неотрицательностью функции f ( s ), s G [ S ⁺ ,S ^- ), то возникают определённые проблемы с определением решения в точках типа s ∗ (рис. 5), то есть в точках смены знака скорости частицы.

/(Sr) > о

.5+           S*1          S" S f№ < 0

Рис. 5. Точка s ∗ скачка скорости лидера со сменой знака, приводящая к «скользящему режиму»

Такая ситуация может возникать в случаях, когда частицам разрешен «задний ход».

Определение решения ДФ-уравнения. Решение ДФ-уравнений (2) будем строить в классе кусочно-линейных неубывающих функций. Тогда под решением ДФ-уравнения (2) для каждого преследователя с номером i + 1 будем понимать функцию — интегральную ломаную, s i +1 : R ^ S, i ∈ N из указанного класса, которая для любого t G [ t ' , t '' ), t '' <  + го удовлетворяет уравнению (2), где [ t ' , t '' ) — интервал определения решения для соответствующего лидера с номером i , а величина t '' даётся представлением (6).

Напомним, что при i = 1 движение лидера задается обыкновенным дифференциальным уравнением с кусочно-постоянной правой частью, и поэтому может быть проинтегрировано независимо от всех других уравнений из (2) ( i ^ 2).

Пусть для пары лидер–преследователь известен алгоритм построения решения для преследователя при известной интегральной ломаной лидера. Очевидно, что в этом случае решения всех уравнений из (2) могут быть построены индуктивно. Построим общий шаг индукции.

Вычисление точек скачков скорости преследователя. Обозначим через { t _n } ^{i +1} множество моментов времени на действительной оси R , где потенциально возможны скачки скорости преследователя с номером i + 1, { t _n } ^{i +1} C [ t ' ,t '' ), i G N . С каждой точкой t _n G { t _n } ^{i +1} могут быть связаны следующие типы событий:

• (а)    событие типа «смена скорости лидера»;

• (б)    событие типа «достижение безопасной дистанции»;

• (в)    событие типа «нарушение безопасной дистанции».

В силу (1) и (2) легко устанавливаются следующие свойства:

если соседние точки скачков скорости преследователя обозначить через t n- 1 и t n ( t _{n -} 1 < t n ), то на интервале [ t _{n -} 1 ,t _n ) график интегральной ломаной преследователя есть отрезок прямой;

каждая точка скачка скорости преследователя имеет место при наступлении либо события типа (а), либо события типа (б), либо при одновременности событий типа (а) и (б);

событие типа (в) наступает только одновременно с событием типа (а).

Заметим, что при наступлении события типа «нарушение безопасной дистанции» скачок скорости преследователя отсутствует, так как безопасная дистанция при смене скорости лидера всегда терпит скачок, а траектория преследователя является непрерывной функцией.

Таким образом, алгоритм вычисления момента времени t _n , соответствующего скачку скорости преследователя (при известном t n- 1 ), основан на сопоставлении моментов времени события типа (а) и события типа (б).

Далее для вычисления точки t n е { t _n } i ⁺¹ при известной точке t n- 1 е { t _n } i ⁺¹ вводим в рассмотрение следующие множества:

T i ⁺¹ ( t n- 1 ) = { п : п> t n- 1 , П е { п }¹} и { t '' } = 0 ,

Ti+1(tn-1) = {t : Ai +1(t) = V(si (tn-1)}, t е [tn-1, min Ti +1(tn-1))} U {t''} = 0, tn-1 е {tn}1+1 c [t',t"), i е N, где {t"} — одноэлементное множество; {n}i — множество точек скачков скорости лидера с номером i,{n}i C [t',t''); а множество

{ t : A i +1 ( t ) = v ( s i ( t n- 1 )) ,...

t е [ t n- 1 , min T i ⁺¹ ( t n- 1 )) } выделяет интервал нулей уравнения

Ai+1 (t ) = v (Si (tn-1)), t е [tn-1, min Ti +1(tn-1)).

Заметим, что введённые множества T η и T ϕ не являются пустыми. Также заметим, что операция вычисления min T i ⁺¹ ( t _{n -} 1 ) выделяет либо точку t" , либо следующую за точкой t _{n -} 1 справа точку скачка скорости лидера с номером i . Операция min T ^ ⁺¹ ( t _{n -} 1 ) выделяет либо точку t" , либо точку, соответствующую событию типа «достижение безопасной дистанции», которая является ближайшей справа к точке t _{n -} 1 или совпадает с t _{n -} 1 .

Пусть вычислена точка tn- 1 е {tn}i+1 i е N. Тогда, учитывая выделенные свойства для событий типа (а), (б) и (в), замечания о вычислении min Ti и min Tv, а также, учитывая, что на любом интервале [tn- 1 ,tn) C [t',t") интегральная ломаная есть отрезок прямой, для вычисления следующей точки tn потенциального скачка скорости преследователя с номером i + 1 получаем рекуррентную формулу

( min { min T i ⁺¹ ( t n- 1 ) , min T ® ⁺¹ ( t n- 1 ) } ,

. _ I        Ai +1(tn-1) = V(Si(tn-1)), tn   I min Ti +1( tn-1),

[       A i +1 ( t n- 1 ) = V ( S i ( t n- 1 )) .

При n = 1 считается, что 1 0 = t ' .

Алгоритм преследования лидера.

Считаем, что на отрезке [ t ' ,t '' ), t '' <  + го построена интегральная ломаная для i -й частицы. Тогда алгоритм построения интегральной ломаной для преследователя с номером i + 1 на отрезке [ t ' ,t '' ) представим в следующем виде:

строится множество V i +1 ( t ' ) = { S i +1 ( t '- ) ,S i ( t ' ) } ;

в силу (2) однозначно вычисляется скорость преследователя s i +1 ( t ' );

строится первый отрезок ломаной с конечной точкой S i +1 ( 1 1 ) = S i +1 ( t ' ) + s i +1 ( t ' )( 1 1 - t ' ), где

{ min { min T i ⁺¹ ( t ' ) , min T ^ ⁺¹ ( t ' ) } ,

Ai+1 (t' )= v (Si (t')), min Ti+1( t'),

A i +1 ( t ' )= v ( S i ( t ' ));

далее считается, что построен отрезок ломаной с номером n - 1; тогда, учитывая, что множество Vi+1(tn-1) = {Si +1(t(n-1)-),Si(tn-1)}, а скорость Si+1 (tn- 1) вычисляется в силу (2), конечная точка n-го отрезка ломаной вычисляется по формуле Si +1(tn) Si+1(tn-1) + 8i+1(tn-1)(tn tn-1), а tn определяется выражением (7). Процесс построения ломаной заканчивается, если при некотором n' < го min{min Ti +1(tn>), min T^ii,+1(tn>)} = t''.

Ясно, что в силу непрерывности ( S i ( t '' ) = S i ( t '- )) имеем

Si +1( t" ) = Si +1( tn' ) + 8 i+1( tn' )(t" — tn'), а точка с координатами (t'',Si+1(t'')) — крайняя справа точка построенной ломаной на плоскости R x S, может быть начальной для продолжения решения при t ^ t''.

В результате искомая ломаная определяется интегралом

^S i +1 ⁽ t ) =

^S i +1 ⁽ t ' ) ⁺ 8 i +1 ⁽ t ' ⁾⁽ t ^— t ' ) ,t ^{е [} t ' ,t 1 ) , ⁿ ( t )

^S i +1 ⁽ t ' ) ⁺      s i +1 ⁽ t m- 1 ⁾⁽ t m    t m- 1 )+

+si+1(tn(tm=1 - tn(t)) ,t е [11 ,t''), tn,t е [11 ,t''), n,m = 1 ,Mi+1, Mi+1 = |{tn}i+11 < го, где n(t) = max{n : tn < t}, tn е {tn}i+1, а моменты времени tn потенциальных скачков скорости преследователя определяются формулой (7). То, что построенная функция Si +1(t) для каждого t е [t' ,t'') удовлетворяет системе (2), проверяется её подстановкой в систему (2).

Некоторые свойства частиц в потоке.

• 1.    Пусть траектории i -го лидера сопоставлена функция s i ( t ) — кусочно-линейная неубывающая функция с конечным числом отрезков прямых, удовлетворяющая (2) для всех t Е [ t ' ,t "), t" <  ж . Тогда движение преследователя s i +1 ( t ) с номером i + 1 с начальным положением s i ₊₁ ( t ' ) < s i ( t ' ) и скоростью s i ₊₁ ( t — ) > 0 однозначно продолжаемо в силу (2) на отрезок t Е [ t ' ,t '' ) ,t '' <  ж в классе неубывающих ломаных с конечным числом отрезков прямых.

• 2.    Переключение скорости преследователя может происходить в моменты времени переключения скорости лидера, а также в моменты времени достижения преследователем безопасной дистанции.

• 3.    На каждом интервале постоянства скорости лидера может быть не более одной точки смены скорости преследователя.

• 4.    Пусть при t = t '

• 5.    Пусть движение частиц в однорядной полосе подчиняется уравнениям (1), (2). Тогда для конечного отрезка однорядной полосы в цепочке двигающихся друг за другом частиц для каждой их пары сохраняется порядок их следования. Таким образом, множество частиц в отрезке однорядной полосы есть параметризованное множество с отношением строгого порядка (транзитивность и антисимметричность), где параметр — текущее время t Е [ t ' ,t '' ) ,t '' <  ж .

тогда для t Е [ t ' ,t '' )

A i +i ( t ) >  0 .

Примеры численного моделирования. На рис. 6 (а) и (б) приведены примеры численного моделирования дискретного потока, представленного ДФ-уравнениями (1) и (2).

^A i +1 ⁽ t ' ) = s i ⁽ t ' ) ^— s i +1 ⁽ t ' ) >  ⁰ ,

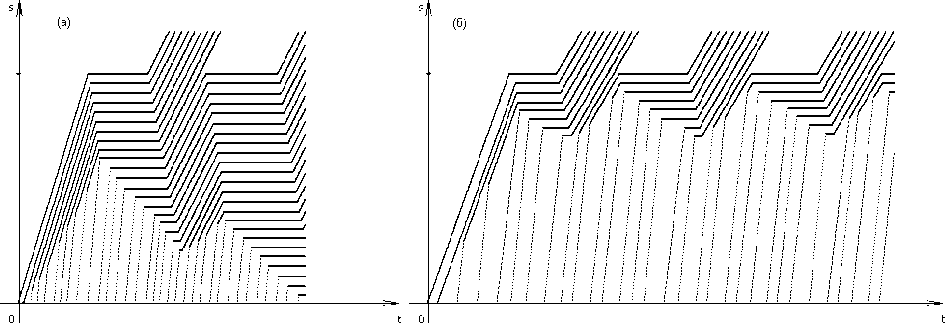
Рис. 6. Результаты численного моделирования очереди частиц: а — случай роста и б — случай стабилизации длины очереди

В плоскости R x S на рис. 6 рассмотрим последовательность t -сечений. Такое рассмотрение легко обнаруживает ранее рассмотренные свойства пробки.

Поток с достаточно большим скоплением частиц становится прерывистым (стоп–старт движение). В таком потоке периодически образуется очередь частиц. На рис. 7 представлен поток в режиме стоп — старт.

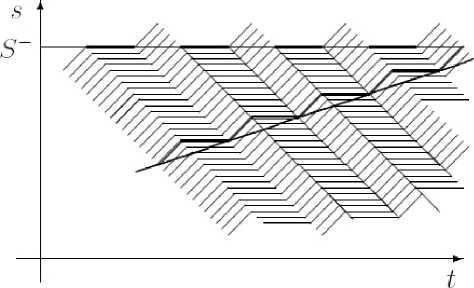
Рис. 7. Поток в режиме стоп–старт

• III.    Замечания о других моделях дискретного потока

О дискретном потоке с импульсным управлением. Исходим из теоремы об изменении количества движения:

mx;( t ) =

t mx( t — At) + j Fd^, t-At где m — масса частицы, rc — её скорость, F — ак-t тивная сила, действующая на частицу, Fdξ — t-At импульс силы на интервале [t — At,t], At > 0.

Пусть равномерно по t существует предел:

lim ( x;(t — A t ) +

A t^ 0

t t-At

Fd^ ) =

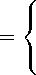
max V ( t ) , ^{s (} t ) , min V ( t ) ,

A( t ) . ( s * ( t)), A( t ) = y ( s * ( t )) , A( t ) . ( s * ( t )) ,

V (t ) = {s( t-) ,s * (t)}, A(t) = s* (t) - s(t), где s* — скорость лидера, s — скорость преследователя, s∗ и s — положения частиц в полосе, а значение предела является правой частью уравнения (2).

В таком представлении наша модель дискретного потока частиц является системой конечного числа материальных точек в канале без трения с импульсным управлением, которые поддерживают безопасную дистанцию между лидером и преследователем.

В случаях ограниченности активных сил, F e [ F - ,F ], где F - и F конечны и характеризуются ресурсом двигателя автомобиля и сцеплением колес и дороги, траектории частиц как материальных точек должны иметь непрерывные первые и ограниченные вторые производные.

При таком представлении вопрос построения уравнений для «гладких» потоков может быть сведен к задаче о сплайновом сглаживании ранее построенных ломаных ([11], с. 168). Особенностью этой задачи (как математической) является следующее. Заданное поле ломанных, образующих дискретный поток, приближается (в некоторой метрике) на классе сплайнов, в котором:

• —    сглаживающие сплайны должны иметь неотрицательную и непрерывную первую производную;

• —    вторые производные — ускорения материальных точек в гладком потоке, должны удовлетворять неравенствам

F <  m s( t ) <  F.

Заметим, что вычислительная сложность задачи связана как с выбором сетки узлов, так и с возможностью построения решения на сплайнах второго порядка.

Далее построенные сглаживающие сплайны рассматриваем в качестве заданных движений материальных точек в потоке. В результате вопрос построения соответствующих управляющих сил может быть сведен к решению так называемой первой (основной) задаче динамики — по заданному движению определить силы его вызывающие ([12], с. 321). Обзор таких задач, трактуемых как построение программных движений, содержится в [14].

Другая трактовка вопроса о преследовании лидера на безопасной дистанции может быть связана с задачей о наложении сервосвязи, введённой А. Бегеным ([13], с. 344). Реализация такой связи (иначе — обратной связи) предусматривает наличие измерителей, силовых приводов и автоматических регуляторов. Обзор алгоритмов стабилиза- ции обратных связей, в частности, использующие скользящие режимы, содержится в работе [15].

Таким образом, с одной стороны, обсуждаемая модель потока на классе кусочно-линейных траекторий является приближением (в указанных смыслах) к потокам механических частиц. С другой стороны, использование на автомобилях форсированных двигателей допускает режимы с быстрым изменением скорости. Кроме того, построение программируемых потоков даёт перспективу перехода на автоматическое вождение автомобилей.

О связи дискретного потока с моделью конечного автомата. Вводим следующие равномерные сетки:

• —    на координатной оси S строим сетку с шагом 5 , 5 = const >  0;

• —    на оси времени R строим сетку с шагом A t ;

• —    вводим конечное множество { v ^m } , v m = m A v , A v = const >  0, m = 0 ,M , M <  ro .

Устанавливаем между шагами сеток следующую связь: A t A v = 5 . Кроме того, функцию ^ ( s i ) заменяем на её дискретное приближение

У ^{( s} i ) δ

] 5.

Г S i ( t о) 1         S i ( t o)

T =

В этом случае предположим, что начальные положения каждой i-й частицы si(tо), i e N, соответствуют узлам δ-сетки, то есть i e N. Кроме того, будем считать, что скачки ско рости лидера цепочки (i = 1) допускаются только в момент времени tk = kAt, k e N, to = 0. Также предположим, что скорости лидера цепочки и всех других частиц (i ^ 2) в сечении входа в отрезок полосы считаются кратными шагу Av ; тогда при всех других tk , k e N, все частицы в силу уравнений (1) и (2) с дискретным временем tk будут располагаться в узлах δ-сетки на координатной оси S.

Пусть M — число узлов в δ -сетке отрезка полосы, а m — число двоичных разрядов, требуемых для записи числа M . Пусть также имеет место равенство log ₂ M = m . Тогда число возможных представлений цепочки частиц в конечной полосе с числом узлом M равно числу 2 ² . Это утверждение следует из факта: множество булевских функций с m переменными равномощно множеству различных цепочек частиц на сетке с M узлами, если только m и M связаны равенством m = log ₂ M .

• IV.    О развитии теории дискретного потока

Алгоритм построения сети. Эскизно наметим алгоритм построения дорожной сети из типовых элементов с их топографическим представлением на декартовой плоскости.

Первый тип элементов — отрезки ориентированных однорядных полос (отрезки полос или кратко ОП). ОП допускают искривления в плоскости и малые их деформации при выводе их из плоскости с целью скрещивания двух и большего числа ОП. Связь отдельных ОП осуществляется через узлы коммутации (кратко — коммутаторы, например, в виде зоны регулируемого перекрёстка двух дорог). В коммутаторах входы одних ОП соединяются с выходами других ОП. Считается, что каждый ОП связан с двумя коммутаторами. Коммутаторы так же, как и ОП, имеют топографическую привязку.

Построенную односвязную область, состоящую из коммутаторов и магистральных отрезков (параллельных и одинаково ориентированных ОП), будем называть магистральной сетью. Эта сеть отделяет друг от друга области, называемые P -зонами. Считается, что в P -зонах допускаются остановки, стоянки и парковки транспортных средств. Также считается, что в P -зонах может существовать собственное внутреннее дорожное устройство. P -зоны формально следует считать открытыми множествами; тогда область, занятая магистральной сетью, будет замкнутой. Заметим, что к P -зонам относится внешняя относительно сети часть плоскости. В магистральную сеть дополнительно врезаются коммутаторы, связываю-щиееёс P -зонами, и, таким образом, решается вопрос связи между собой всех P -зон.

Построение сети может быть завершено прокладкой допустимых маршрутов между P -зонами. Маршруты на карте сети выделяются маршрутными нитками, которые можно рассматривать как допустимые траектории движения транспортных единиц.

Отметим принципиальную особенность коммутатора. Его коммутационная зона покрыта «паутиной» ниток — траекторий, соединяющих входящие и выходящие ОП, примыкающие к коммутатору. Поэтому тактовое действие светофорного регулятора может быть представлено следующим образом: попеременное открытие и закрытие движения по отдельным группам траекторий, при котором в каждый момент времени исключаются точки пересечения ниток.

Маршрутизация как алгоритмическая проблема. Построенную сеть со светофорным регулированием наполним подвижной дискретной средой — потоками частиц, которые локально подчиняются закону безопасной дистанции. В результате получаем новый объект. Этот объект, с одной стороны, является топографическим представлением дорожной сети, которое напоминает ориентированный граф. С другой стороны, дискретная среда частиц, помещённая в сеть, создаёт совокупный поток, действие которого должно подчиняться следующим целевым установкам:

• — каждая частица должна реализовывать свою, установленную ею самой, последовательность прохождения P -зон;

• — управление совокупным потоком этих частиц должно устойчиво блокировать образования заторов.

Дискретная среда может содержать порядка 10 ⁷ частиц, поэтому вопрос выбора маршрутов для каждой частицы является весьма трудоемкой задачей. В этом контексте проблему маршрутизации следует рассматривать как алгоритмическую, например, как задачу о существовании некоторого единого правила прокладки маршрутных ниток между любыми парами P -зон.

Тезисно выделим ряд базовых вопросов в теоретических исследованиях нового объекта.

— Аксиоматика сети, связанной с её топографическим и теоретико-графовым представлениями, а также алгоритмов сетевой сборки.

— Способ варьирования сети; в том числе деформации сети, например, преобразование поперечно-продольной схемы в радиально-кольцевую; преобразование сети при включениях и удалении сетевых элементов; топологические характеристики и критерии сравнения сетей с оценкой сложности их маршрутно-ниточного покрытия.

— Теория коммутатора, включающая модели прохождения и преобразования частиц в коммутаторах потоков; модель светофорного регулирования в коммутаторе; механизмы формирования заторов в площади коммутатора.

— Краевые условия на границах ОП и коммутаторов; общие уравнения дискретных потоков, условия существования сетевых напряжённых потоков.

— Полнота данных в задаче управления потоками частиц; принципы и оценки возможных ресурсов управления.

В заключение подчеркнем, что новый объект — сеть с вложенными в неё дискретными потоками частиц — может быть полезен при разработке других общесетевых тематик, в том числе при проектировании вычислительных наноструктур.