К теории термопар

Рассмотрены вопросы формального (математического) описания процессов в термопарах как с позиций механизма контактной термо-ЭДС, так и с позиций эффекта Томсона. Показано, что конечные соотношения с точностью до обозначений получаются одинаковыми для обоих механизмов.

В системах управления микроклиматом зданий для измерения температуры широко используются термоэлектрические термометры, содержащие в своем составе термопару. Термопары являются базовым элементом термоэлектрических генераторов, используемых напрямую для получения электрической энергии, а также и так называемых термоэлементов, применяемых, например, в холодильной технике и в термоэлектрических тепловых насосах [1]. Поэтому изучение и выявление всех сторон и особенностей термоэлектрических процессов в термопарах имеет достаточно большое значение.

Как показал анализ литературных данных, до настоящего времени нет единого общепринятого представления о причинах возникновения термо-ЭДС термопары. Обычно для объяснения принципа действия термоэлектрического термометра привлекают несколько механизмов, чаще всего выделяют два явления [2-4]: 1) механизм контактной термо-ЭДС (эффект Зеебека); 2) эффект Томсона. Несмотря на различную природу данных эффектов, как нам удалось выяснить, формальное описание процессов в термоэлектрических цепях получается совершенно одинаковым. Вместе с тем, насколько нам это известно, в литературе эта тождественность описаний до настоящего времени не была достаточно отчетливо показана [2-10], поэтому есть смысл подробнее остановиться на этом вопросе. При этом подчеркнем, что указанный вопрос является достаточно важным, поскольку в учебной литературе по измерительной технике обычно упоминался механизм контактной термо-ЭДС [5-8] и поэтому все основные свойства термопар были описаны и обоснованы с позиций этого явления.

К месту заметим, что значимость эффекта Томсона до сих пор еще подвергается сомнению [1, с. 15 и с. 128], однако в данной работе мы не будем непосредственно обсуждать этот вопрос.

Отметим также, что возможно именно по причине недостаточной ясности в описании процессов в двух недавно изданных учебниках по теплотехническим измерениям и приборам [9, 10] это формальное описание просто опущено, в [10, с. 60], например, первое свойство термопар фор мулируется «без доказательства», что вообще-то не является лучшим выходом из создавшегося положения.

Рассмотрим цепь, состоящую из двух разнородных проводников Р я О (рис. 1).

Рис. 1. Термопара

Как это хорошо известно, в данной цепи контактные термо-ЭДС образуются в точках 1 и 2, обозначим их как Ерд^ и Е^(Г₂). Результирующая контакная ЭДС цепи (см. рис. 1) будет равна

Ек х 1⁼ Ерд ft)⁺ Eqp (?₂ )

(направление обхода контура против часовой стрелки, порядок чередования индексов соответствует этому направлению), здесь и Z2 - температуры контактов. На основании закона Вольта [5] можно записать, что

EpQ^t^-v Eq_PQt^=Q , поэтому

^Х1 - Ерд (?1) - Ерд (t₂ ) .

Теперь рассмотрим отдельно однородный проводник, пусть, например, это будет проводник Q и пусть его длина равна L . Выделим по длине этого проводника малый участок dx , тогда термо-ЭДС Томсона, генерируемая на этом участке, будет равна dEg—kg^f^—^dx, где кд(Р) - коэффициент Томсона для проводника Q. Очевидно, что термо-ЭДС Томсона для всего проводника Q будет определяться как

E_Q = \k_Q^dx= \k_Q^dt=F_Q^ ^Fq^-Fq^.

Здесь Fq^ - первообразная для кд(Р), т.е. dF₀(t)

—~—~k0{t). Из этого выражения отчетливо dt видно, что термо-ЭДС Томсона зависит только от температуры концов проводника Q и не зависит от температуры других его точек. Кроме того, термо-ЭДС Томсона зависит также и от рода проводника, так как коэффициент Томсона kg(f) и первообразная для него Fg(t) определяются именно родом проводника.

Для проводника Р по аналогии можно записать, что

ЕР= FpQt^-Fplt^, здесь контур (см. рис. 1) также обходится против часовой стрелки, поэтому для проводника Р начальной точкой будет уже точка 2 . FP (?) - первообразная для коэффициента Томсона проводника Р . Таким образом, суммарная термо-ЭДС цепи рис. 1, обусловленная эффектом Томсона, будет равна

Етг\= Fg(,t2)- Fg(tx)+FP(tx)-FP(t2)=

= [FP(t})-FQ(tx)^

= Fpg^-FpgQt-^ , где Fpg^-Fp^-FgCjy Отсюда следует, что Етгх также как и Ет зависит только от рода проводников и температуры их спаев. Причем отметим также, что конечные выражения для Ет и Ега одинаковы с точностью до обозначений.

Как известно, свойства термопар также ранее были описаны и обоснованы с позиций контактной термо-ЭДС, поэтому рассмотрим и эти моменты.

Свойство 1: если в цепь термопары включен третий проводник и его концы находятся при одинаковых температурах, то результирующая термо-ЭДС цепи не изменится.

Рассмотрим первый возможный способ включения третьего проводника (на схеме это проводник R ) в цепь термопары - в разрыв второго контакта проводников Р и Q. При таком включении третьего проводника температуры мест его подсоединения должны быть, конечно, равны t₂. Для исходной термопары, изображенной на рис. 1, результирующая контактная ЭДС будет равна

ЕкП ⁼Epg(t_x)-Epg(t₂) , для термопары с третьим проводником (рис. 2)

^12 ⁼ Epg(t_x) + Eg_R(t₂) + Ерр^з) .

R

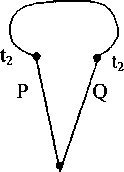
tl

Рис. 2. Первый способ включения третьего проводника в цепь термопары

Если в цепи с третьим проводником температуры всех контактов будут одинаковы и равны t₂, то на основании закона Вольта можно записать

Epg(t₂) + Едр^₂} + Epp(t₂) = Q , следовательно

EQR^+Epp^-Ерд^ .

Подставляя это соотношение в формулу для Е_кИ, получим, что

Ек^2~ЕРд(1х)-EPg(t2) , т.е. EkS2 = EkXX. Если теперь считать, что в цепи (см. рис. 2) проявляет себя только эффект Томсона, то получим, что

EpL2= Fg(t2)~ Fg(t^ + FR(t2)~ FR (,<->)+

■^Ер^)-Fp(t2)= Fpg(tx)-Fpg(t2) , т.е. £r22 =ET£ ]. При этом заметим, что для получения конечного результата не потребовалось привлекать какие-то дополнительные данные, в том числе и закона Вольта.

Далее, рассмотрим второй возможный способ включения третьего проводника в цепь термопары -в разрыв одного из проводников, например, Q.

При таком включении третьего проводника температуры мест его подсоединения должны быть равны между собой, но совсем не обязательно должны быть равны ?2 • В данном случае контактная термо-ЭДС

ЕкХЗ ⁼ Ерд (/] ) + Едр (?з ) + Ерд (t₃ ) +Едр (t₂) , но ведь

Ерд(^$з) ⁼ ~Eg_R(t₃), поэтому

Ек^З ⁼ Ерд Д ) +Едр (t₂ ) = Ерд (?) ) - Ерд (t 2 ), т.е. равна ЭДС исходной цепи.

Если теперь считать, что в цепи (рис. 3) также проявляет себя только эффект Томсона, то получим, что

Ерхз ~Fg(t3)-Fg(t1)+Fp(t3)-Fp(t3)+Fg(t2)-

-Fg(t3) + Fp(t1)-Fp(t2)= Fpg(tX)- Fpg(t2) .

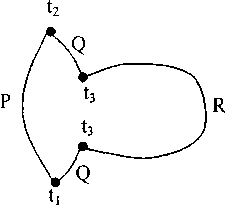
Рис. 3. Второй способ включения третьего проводника в цепь термопары

Таким образом, доказательство справедливости свойства получилось заметно проще. К месту заметим, что доказательство других двух известных свойств термопар [5-10] с позиций эффекта Томсона получается также достаточно простым и естественным.

В целом, все вышеизложенное, как нам представляется, может служить неким теоретическим доказательством законов термоэлектрических цепей. В [2, с. 12], по-видимому, из-за отсутствия отчетливого формального описания и обоснования эти законы (правила) названы только «экспериментальными».

Выводы. Рассмотрены вопросы формального (математического) описания процессов в термопарах как с позиций механизма контактной термо-ЭДС, так и с позиций эффекта Томсона. Показано, что конечные соотношения с точностью до обозначений получаются одинаковыми для обоих механизмов. Поэтому достаточно уверенно можно пользоваться теми формулами и свойствами для термо-ЭДС, которые исторически первыми были получены и обоснованы для механизма Зеебека, при этом, конечно, следует напоминать, что вид этих формул соответствует одновременно и эффекту Зеебека и эффекту Томсона.