К теории упругости микронеоднородных сред, учитывающей стохастические изменения связности составляющих компонентов
Автор: Сараев Л.А.
Статья в выпуске: 2, 2021 года.
Бесплатный доступ
Предложена математическая модель расчета эффективных модулей упругости микронеоднородного двухкомпонентного изотропного композиционного материала, связность компонентов которого изменяется случайным образом в зависимости от уровня их относительных объемных содержаний. Сформулировано стохастическое уравнение для параметра связности составляющих компонентов, согласно которому при увеличении объемного содержания наполнителя отдельные включения образуют структуры матричной смеси в виде взаимопроникающих каркасов, а затем превращаются в новую связующую матрицу с отдельными включениями из материала остатков старой матрицы. Алгоритм численного решения этого стохастического дифференциального уравнения построен в соответствии с методом Эйлера - Маруямы. Для каждой реализации этого алгоритма строятся соответствующие стохастические траектории для случайной функции связности составляющих компонентов композиционного материала. Разработан вариант метода расчета математического ожидания случайной функции связности составляющих компонентов и получено для него соответствующие дифференциальное уравнение. Показано, что численное решение этого уравнения и среднее значение функции фактора производства, вычисленное по всем реализациям стохастических траекторий, дают близкие численные значения. Установлены новые макроскопические определяющие соотношения для микронеоднородных материалов с изменяемой микроструктурой и вычислены их эффективные модули упругости. Отмечено, что формулы для этих эффективных модулей упругости обобщают известные результаты для изотропных композиционных материалов. Значения эффективных модулей упругости, построенных по полученным в статье выражениям, лежат внутри вилки Хашина - Штрикмана для нижней и верхней границы эффективных модулей упругости композиционных материалов. Численный анализ разработанных моделей показал хорошее соответствие известным экспериментальным данным.
Включения, композит, компоненты, макроскопические свойства, матрица, матричная смесь, модули упругости, связность, статистическая однородность, микроструктура, эргодичность, эффективные соотношения
Короткий адрес: https://sciup.org/146282044
IDR: 146282044 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.2.12
Текст научной статьи К теории упругости микронеоднородных сред, учитывающей стохастические изменения связности составляющих компонентов
ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2021PNRPU MECHANICS BULLETIN
Развитие методов расчета эффективных характеристик перспективных дисперсно-упрочненных композиционных материалов со случайной микроструктурой представляет собой актуальное направление современной механики деформируемого твердого тела. Подобные конструктивные материалы, наполненные высокопрочными и высокомодульными дисперсными частицами, структурно неоднородные порошковые стали и сплавы проявляют высокие механические и прочностные свойства, благодаря которым они широко применяются в машиностроении, в теплоэнергетическом комплексе, медицине и других отраслях.
Для расчетов эффективных характеристик упругих свойств композиционных материалов существует ряд классических, структурно-феноменологических методов и подходов, использующих модули упругости компонентов и их объемные содержания [1–9].
На основе этих методов были разработаны их модификации и построены модели композиционных материалов с различной степенью связности составляющих компонентов [10–19].
Эти модели достаточно адекватно описывают упругие свойства дисперсно-упрочненных композиционных материалов, содержащих хаотически распределенные высокопрочные и высокомодульные частицы и наноструктурные элементы, пластиков, наполненных стеклянными микросферами и т.д. [20–26].
Кроме того, подобного рода модели способны давать достаточно точные оценки модулей упругости пористых металлов, металлокерамики, полимеров и строительных материалов [27 –36].
Во всех отмеченных выше моделях дисперсные частицы или поры представляют собой отдельные включения, распределенные в связующей матрице. Значения эффективных модулей упругости зависят только от значений модулей упругости составляющих компонентов и их объемных содержаний. Экспериментальные исследования упругих свойств конструкционных композиционных материалов показывают, что при технологическом изготовлении образцов композитов путем прессования, брикетирования, спекания и пропитки расплавом связующего компонента, при одних и тех же значениях модулей упругости составляющих компонентов и их объемных содержаний, макроскопические эффективные модули упругости изготовленных образцов композитов практически всегда проявляют определенный разброс их свойств [37, 38].
Это связано с особенностями изготовления образцов композитов. Многочисленные исследования внутренней структуры дисперсно-упрочненных композитов показывают, что при достаточно большом объемном содержании наполнителя отдельные включения, спекаясь, образуют структуры матричной смеси в виде взаимопроникающих каркасов. В предельных случаях дисперсные частицы могут образовать новую связующую матрицу с отдельными включениями из материала остатков исходной матрицы [39].
Целью исследования является разработка модели расчета эффективных модулей упругости микронеодно-родного двухкомпонентного изотропного композиционного материала, учитывающей случайный характер изменений связности его компонентов в зависимости от уровня их относительных объемных содержаний.
-
1. Постановка задачи
Пусть упругий изотропный двухкомпонентный композиционный материал занимает объем V , ограниченный поверхностью S . Законы Гука материалов его компонентов имеют вид
-
s , (r) = 2 •№s • e (r); cpp =3 • Ks •£pp; r e V; (s = 1,2).
Здесь sj = CTj- — ~ -5 J • CT pp , ej = £ i - - • 5 i ■ £ pp , Cj,
- тензоры напряжений и деформаций, V - объемы составляющих компонентов ( V + V = V ) ; r = ( x , хг, х 3 ) - радиус-вектор координат, ц, - модули сдвига, K -объемные модули компонентов. Для определенности будем считать, что ц2 > ц и K > K ■
Геометрические особенности структуры такого композита могут быть описаны случайными индикаторными функциями координат ks ( г ) , каждая из которых равна единице в точках объема V и равна нулю в точках вне этого объема. Для описания связности составляющих компонентов композиционного материала введем неопределенные модули упругости тела сравнения ц и K , удовлетворяющие неравенствам № 1 <№<№ 2 ; K 1 < K < K 2 [1].
С помощью функций к ( г ) и модулей ц и K закон Гука (1) запишется в виде
/i ( r ) = 2 •№• e j ( r ) + 2 - ( [ № 1 ]-к 1 ( r ) + [ № 2 ] - K 2 ( r ) ) • e j ( r ) , (2)
C pp (r ) = 3-K-£ pp (r) + 3-([K1 ]-K1 (r) + [K2 ] -K2 (r ))-£ pp (r ), где [№s] = №s-№; [Ks]= Ks -K ■
Все физические и геометрические поля рассматриваемой задачи предполагаются случайными, статистически однородными и эргодическими полями, и их математические ожидания заменяются средними значениями по соответствующим объемам [1-4]
(A = F J f ( r )- d r ; fA = 'J f ( r )- d r ■
V V V s Vs
Здесь угловыми скобками обозначена операция статистического осреднения.
Для установления макроскопических определяющих уравнений и вычисления эффективных характеристик рассматриваемого композиционного материала необходимо найти связь между макронапряжениями ^ C ^ и макродеформациями £ £y ^ , которая в самом общем случае имеет вид
(CiJ ) = E ijkl " (£ kl ) , (3)
где E*u - тензор эффективных модулей упругости композиционного материала.
Для установления макроскопических определяющих уравнений (3) и вычисления эффективных характеристик необходимо усреднить по полному объему V локальный закон Гука (2)
£si ) = 2 •№• ( e i, )+ 2 - ( [№ 1 ] - с 1 - eey 1 + +[№ 2 ] - с 2 - eey )2 ) ,
(ст ) = 3• K Ve W3-f[ K . 1- с . Ve ) + Г ^ 21- с, Ve \ У
\ pp / \ pp/ \L 1J 1 \ pp /1 L 2J 2 \ pp j^ p
V где cs = — - объемные содержания составляющих компонентов. Таким образом, для решения задачи необходимо выразить деформации ^ £ц ^ через макроскопические деформации £stj ^ ■
Получение соотношений (4) достигается статистическим осреднением системы уравнений, состоящей из закона Гука (2), уравнений равновесия
C p , p ( r ) = 0 ’ (5)
и формул Коши
-
2 -£ i ( r ) = u i, J ( r ) + u , i ( r ) , (6)
-
2. Модули упругости композиционного материала со стохастической связностью составляющих компонентов
связывающих компоненты тензора деформаций £у (r) с компонентами вектора перемещений u (r). Граничные условия отсутствия флуктуаций величин на поверхности S объема V f (r )| reS =£ f^ ■ (7)
Исключение из системы уравнений (2), (5), (6) компонентов тензоров напряжений и деформаций дает систему равновесия микронеоднородной среды в перемещениях [5-7]
№• « ' pp ( r ) +( K + №j- u p , pi ( r ) -T p , p ( r ) = 0 , (8)
где
T j = t j + ^5 u "T pp ,
t j -- 2 '^■ ( ( m l - 1 )’K 1 + ( m 2 - 1 )'K 2 ) " e ij ’
T PP -- 3 ^ K ■ ( ( k 1 - ^K + ( k 2 — ^K J^ pp ’
m 1
= E1 m = E l k Kk K 2
ц ’ m 2 ц ’ k 1 K ’ k 2 K ’
штрихами обозначены флуктуации величин в полном
объеме V .
С помощью тензора Грина
G ik ( r ) -
—1 8 i 8 ■л^ц (
. pp
3 ■ K + 5 ■ц
3 ■ K + 8 ■ц
содержащего неопределенные модули упругости тела сравнения ц и K , система уравнений (8), (9) сводится к системе интегральных уравнений, ядрами которых служат вторые производные тензора Грина [8]
есть эффективные модули упругости рассматриваемого композита.
От выбора вида модулей упругости тела сравнения ц и K зависит способ взаимодействия между собой составляющих компонентов и их участия в несущей способности композиционного материала. Выбирая определенным образом величины ц и K , можно получать различные варианты моделей композиционных материалов, обладающих разной степенью связности составляющих компонентов.
Если, например, в общих формулах (14) положить ц - ц , K - K , то получится модель композита, в котором первый компонент играет роль связующей матрицы, а второй компонент – роль отдельных включений. Выражения для эффективных модулей упругости (14) принимают вид
*
ц l -ц 1 ■
1 +
е j ( r ) - f G k , l ( r - г ) 'T ki ( г | ■ d r 1 . (10)
V
с 2 ■ ( m - 1) 1 +a, ■ с ■ ( m - 1)
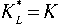
Величины (е.) находятся из известных соотноше- \ У /2
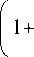
с 2 ■ ( к - 1)
1 + Y 1 ■ C 1 ■ ( к - 1)
ний [8, 9]
где
( £ ) = ( £ ) + Г (K*f*£)
\ еИ \ еИ 1 c) \ К0 еИ .
\ У / 2 \ У / 2 \ 2 У /
Для вычисления случайных моментов к^е’. у необходимо умножить уравнения (10) на к‘ ( г ) , усреднить их по полному объему V и воспользоваться свойством изотропности функции к‘ ( г ) [8]
1 1 + «■( m -1) у j'2 1 + «■((m -1) + с ■(m2 -т)) ' j
. \ 1 + Y< k 1 - 1 )
—■ е pp'2 1 +Y-((k1 -1) + с ■(k2 -k1 )P pp'
2 4-5"У. 1 1 + v. 1 3■ K. -2■ц, a. ---1; y, ---L; v, ---1---------1,
-
1 15 1 -vj 1 3 1 -v 1 2 3 ■ K + 2 ^^
ц2
m - —;
H 1
к - K 2 K 1
Если же в общих формулах (14) положить ц - ц2 , K - K2, то получится модель композита, в ко- тором, наоборот, второй компонент играет роль связующей матрицы, а первый компонент – роль отдельных включений. В этом случае выражения для эффективных модулей упругости (14) принимают вид где
2 4-5■v 1 1 + v 3■ K-2■ц a ----; y ----; v - —------------.
15 1 -v 3 1 -v 2 . ( 3 ■ K + 2 ■ ц )
*
ц H -ц 2 ■
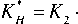
Подставляя формулы (12) в выражения (4), получаем макроскопический закон для рассматриваемого ком-
где
с 1 ■ (1 - m )
m + a 2 ■ с 2 ■ (1 - m )
1 +
с 1 ■ (1 - к )
q +Y 2 ■ с 2 ■ (1 - к )
позита ssj ]=2-ц* ■ e),
(npp)-3■K -(epp)’ где
2 4 - 5 ■v, 1 1 + v2 1 3 ■ K - 2 ■ц2
a2 -----2 , Y-> -----2 , v-> -----2---------2 .
-
2 15 1 -v2 2 3 1 -v2 2 2 3 ■ K 2 + 2 '^
Для допущенных ранее неравенств цг > Hi и K 2 > K формулы (15) представляют собой нижние
* ц
- ц ■ m + I
c 2 ■ ( m 2 - mx ) ■ ( 1 + a ■ ( mx - 1 ) ) 1 + «■ ( ( mx - 1 ) + c ■ ( m 2 - mx ) )
K * - K ■ k
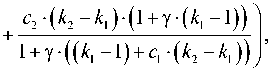
границы, а формулы (16) – верхние границы Хашина – Штрикмана для изотропных эффективных модулей упругости. Эти границы следуют из известных теорем теории упругости о минимуме потенциальной энергии и минимуме дополнительной энергии и являются существенно более узкими, чем границы Фойгта и Рейсса
где
<
Ц R < ц * < ц F , Kr < K * < Kf ,
, ц ■ ц2
ц F = C 1 ■ц + c 2 -М 2 , ц R =------------- c i - Ц 2 + c 2 ■ц
KF = c ■ K, + c 2 ■ K , KR =-----1---2---
F1122 R c1 ■ K2 + c2 ■ K1
На рис. 1 показаны верхние и нижние границы Фойгта и Рейсса для эффективного модуля упругости сдвига, рассчитанные по формулам (18), верхние и нижние границы Хашина – Штрикмана, рассчитанные по формулам (15) и (16), и кривая модуля упругости сдвига для матричной смеси, рассчитанная по формулам (19).
ц
Другим типом связности составляющих компонентов обладает микронеоднородная среда, у которой матрица взаимопроникающими компонентами. Модули упругости такого композиционного материала получаются из общих формул (14), если в них положить
{ ц) = C l -H l + c 2 -М 2 ,
(K) = C i ■ K 1 + c 2 ■ K 2 .
В этом случае выражения для эффективных величин (14) принимают вид
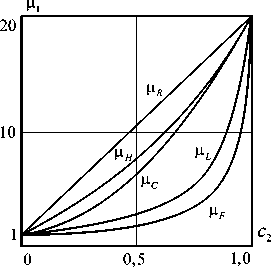
Рис. 1. Графики функций верхних и нижних границ Фойгта и Рейсса для эффективных модулей упругости сдвига, рассчитанных по формулам (18), верхних и нижних границ Хашина – Штрикмана, рассчитанных по формулам (15) и (16), и кривая модуля упругости сдвига матричной смеси, рассчитанная по формулам (19)
где
H e = (ц)-
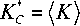
«■ ( ц2 -Hi ) 2 ■ c ■ c2
{ц^а^ц-H i ) ■ ( c i - c 2 )’
H K 2 - K i ) 2 ■ c i ■ c 2
(K + Y- ( K 2 - K i ) • ( c i - c 2 )
2 4 - 5 Vv) 1 i + (v) . .
a =--- tV ;в =---^-; M =
I5 i-(v) 3 i-(v) X 1
3 4 K - 2 ■И
6 ■ ( K + 2 4ц).
Fig. 1. Graphs of the functions of the upper and lower Voigt and Reuss boundaries for the effective shear elastic moduli calculated by formulas (18), the upper and lower Hashin – Shtrikman boundaries calculated by formulas (15) and (16), and the shear modulus curve of the matrix mixture calculated by formulas (19)
Из формул (19) для эффективных модулей упругости видно, что каждый компонент обладает самостоятельной несущей способностью и не представляет собой набор отдельных включений. Так, например, при ц = K = 0 макроскопические величины ц * , K * тождественно в нуль не обращаются. Тот факт, что рассматриваемый композит представляет собой матричную смесь, подтверждает инвариантность формул (19) относительно одновременной перестановки величин ( c i , ц 1 , K i ) и ( c 2 , ц 2 , K 2 ) .
Если в соотношениях (14) принять ц = ц * ; K = K * , то относительно эффективных модулей упругости многокомпонентного композита получаются уравнения так называемой самосогласованной модели
Расчетные значения: ц = i; vj = 0,35 ; ц2 = 20; v2 = 0,25.
В самом общем случае вид неопределенных модулей упругости тела сравнения ц и K может быть представлен соотношениями
ц = ц и = u i ( c i ) ■Ц i + u 2 ( c 2 ) ^ц 2 , K = K u = U i ( c i ) ■ K i + и 2 ( c 2 ) ■ K 2 ,
где
*
a
<
c i ■ц
** *
Ц s + a s "( ц-^ )
c 2 ■ ц 2
** *
ц S + a S ■ (ц 2 ц S )
= i,
c i ■ K i 1 c 2 ■ K 2
* * * * * *
K S +Y S ■ ( K i - K S ) K S +Y S ■ ( K 2 - K S )
= i,
где величины u ( c ) , u 2 ( c 2) - монотонно возрастающие функции, описывающие связность составляющих компонентов композитов и удовлетворяющие условиям
0 < U i ( c i ) < i, U i ( 0 ) = 0, U i ( i ) = i,
< 0 < u 2 ( c 2) < i, u 2 ( 0 ) = 0, u 2 ( i ) = i, u ( c ) + u 2 ( c 2) = i.
Подстановка величин (21) в соотношения (12) позволяет получить формулы для усредненных по объему V деформаций
2 4 - 5 ■v*_,*_i i +v*_,*_3 ■ K * - 2 ■ц*
■ ~* ; У s = т ■ *"; v s = r * n г.
i5 i -v 3 i - v2 6 ■ K o + 2 ■ ц.
S S SS
(ei?) = (i + a и ■ ( m u - 4)^ и ■ ^eij ),
2 (22)
(s pp x = (i +y и -( k - OXn и -4 pp) .
Формулы (14) для эффективных модулей упругости принимают вид
* u
Ц U = Ц „ • m l +
K = K u • k u +
c 2 • ( m u - m u ) - ( l +a u •( m u - 1 ) ) ^ 1 + a u ■ ( ( m u - 1 ) + c l • ( m u - m u ) ) ? C 2 • ( k I - k u ) ^ ( 1 + Y u ■( k u - 1 )) ' 1 + Y u • ( ( k u — 1 ) + C • ( k u — k u ) ) , ,
где
|
2 4 - |
■ 5 •V u -v |
1 |
1 + V u ... |
3 • -u - |
- 2•Ц u . |
|
“ u 15 1 |
; Y u -V u |
3 |
1 ; u '■'I 1 -V u 2 |
• ( 3 • - u |
+ 2 ^ u ) (24) |
|
m u = |
^^ ; m u = |
Ц2. ; |
u , k u = ; k u |
Ku =---- . |
|
|
1 |
Ц u |
Ц u |
1 Ku 2 |
K u |
На практике изготовление дисперсно-упрочненных композиционных материалов обычно сопровождается прессованием, брикетированием, спеканием дисперсных частиц и пропиткой расплавом связующего компонента. При малых объемных содержаниях второго компонента композиционного материала c распределенные в объеме первого компонента V дисперсные частицы практически не влияют друг на друга, их взаимодействие между собой и связность будут минимальными. В этом случае основной вклад в несущую способность композиционного материала обеспечивает первый компонент, образуя связующую матрицу, в которой хаотически распределены дисперсные включения второго компонента, а функция связности u 2 ( c 2) будет принимать малые значения, сравнимые со значениями величины c . С ростом объемного содержания второго компонента его брикетируемые и спекаемые дисперсные частицы образуют структуры, которые вместе с материалом первого компонента формируют взаимопроникающие друг в друга каркасы. При этом взаимодействие дисперсных включений в этих каркасах существенно увеличивается и сопровождается соответствующим ростом функции связности u 2 ( c 2) и ее производной.
При объемных содержаниях второго компонента композита c , близких к единице, компоненты композиционного материала могут меняться ролями. Основной вклад в несущую способность композита начинает вносить материал второго компонента, формируя связующую матрицу, в которой хаотически распределяются включения из материала первого компонента, а функция связности u 2 ( c 2) начинает принимать значения, близкие к единице.
Многочисленные экспериментальные наблюдения показывают, что при технологическом изготовлении образцов дисперсно-упрочненного композиционного материала для одних и тех же значений объемных содержаний дисперсных частиц c эффективные модули упругости принимают различные значения. Это свидетельствует о случайном характере формирования внутренней структуры композитов, поэтому функцию связности u2 (c2) необходимо считать случайной величиной.
Очевидно, что изменение функции связности u2 (c2) должно соответствовать изменениям объемов компонентов V и V . Так, например, уменьшению объема первого компонента будет соответствовать увеличение функции связности u2 (c2), и наоборот. Таким образом, естественно предположить, что положительное приращение функции связности Аu2 > 0 будет про- порционально относительному приращению первого
А V компонента Аю =--1 > 0.
V 1
Относительное приращение Аю связано с прира щением А с2 соотношением
А V А V А ( с 2 • V ) А с, А с.
Аю =--1 = —2 = —----- = —2 =--— .
V V с • V с 1 - с2
Таким образом, переменные Аю и Ас2 связаны уравнением или d ю =
dс
1 - с2 ’
с2 = 1 - exp ( -ю ) .
Здесь использовано очевидное начальное условие с2| = 0.
2 1ю=0
Приращение функции связности А u 2 ( ю ) =
= u 2 ( ю + Аю ) - u 2 ( ю ) на некотором промежутке Аю можно представить в виде трех слагаемых:
А u2 = А u A + А u B + А u W . (26)
Здесь А u A - частичное приращение функции связности на отрезке Аю за счет слабого взаимодействия отдельных частиц; А u B - частичное приращение функции связности на отрезке Аю за счет существенного взаимодействия отдельных частиц, образующих каркасные структуры; А u W - случайные колебания приращения функции связности на отрезке Аю за счет воздействия случайных внешних факторов при технологическом изготовлении образцов дисперсно-упрочненного композиционного материала.
Величины А u A , А u B , А u W можно представить в виде
А u A ( ю ) = A ^ ( 1 - u 2 ( ю ) ) ^Аю ,
< А u B ( ю ) = B • u 2 ( ю ) • ( 1 - u 2 ( ю ) ) ^Аю , (27)
А u W ( ю ) = О^ u 2 ( ю ) • ( 1 - u 2 ( ю ) ) • е ( ю ) • А w .
Здесь A – коэффициент, описывающий взаимодействие включений при их малых объемных содержаниях; B – коэффициент, описывающий интенсивное взаимодействие между собой включений и формирование из них групп каркасных образований; w – стандартный винеровский процесс; A w = е ( го ) -4Кго , о - среднеквадратичное отклонение функции связности и2 ( го ) от своего математического ожидания; функция
е ( го)~ N ( 0,1 ) - случайная величина с нормальным законом распределения, нулевым средним значением (е) = 0 и единичной дисперсией (е2) = 1 [40].
Множитель ( 1 - и - ( го ) ) соотношений (27) соответствует замедлению роста функции связности и2 ( го ) , при котором достаточно большая совокупность включений и связующая матрица образуют взаимопроникающие каркасы. Параметр X описывает интенсивность стремления функции ( 1 - и - ( го ) ) к своему предельному нулевому значению.
Подстановка формул (27) в соотношение (26) дает
A u2 (го) = ((A + B - u2 (го))- Аго+о и2 (го)-е (го)-Aw )х х(1 - u2-(го)).(28)
Предельный переход в уравнении (28) при Аго ^ 0 и A w ^ 0 приводит к стохастическому дифференциальному уравнению диффузии Ито [40]
du2 = P (и2) - d го+ Q (и2) - dw.(29)
Здесь
P (u2 ) = ( A + B - u )-(1 - u2•)
– коэффициент сноса уравнения (29),
Q (и2 ) = о- и2 -е-(1 - и •)
– коэффициент волатильности уравнения (29).
Начальное условие для уравнения (29) с коэффициентами (30) и (31) имеет вид u2 (0)= 0 ,(32)
щью алгоритма, построенного в соответствии с методом Эйлера –Маруямы [40]
ГЛ и и 2)+ ( A + B - и . |-+
V
+ о- и (1) -е ( c (1 ) ) -
А c ( i ) ^1 ( ( i
'( 1 - ( и 2 )) ) .
При реализации алгоритма (34) на малом шаге A c ( i ) > 0 начиная с нулевого значения генерируется случайное число е( i ) =е ( c ( i ) ) и вычисляется последующие значение и ( i + 1 ) . Результатом работы этого алгоритма образуются последовательности { c 2 i ) } и { и 2 i ) } , которые на координатной плоскости образуют систему точек { c 2 i ) , и 2 i ) } и соответствующую ей случайную траекторию. Каждый раз при повторении алгоритма (34) образуется новая случайная траектория, поскольку случайная величина е = е ( c 2) генерирует новые случайные значения.
В численных расчетах по алгоритму (34) отрезок c е [0,1] разбивался на n = 100 одинаковых частей с постоянным значением шага A c ( i ) = A c2 = 0,01. Число реализаций случайной функции связности и 2 ( c 2) было принято m = 50. Следует отметить, что вблизи начальной точки { c 20 ) = 0, и 20 ) = 0 } и вблизи конечной точки { c 2 n + 1 ) = 1, и 2 n + 1 ) = 1 } функция связности становится почти детерминированной.
Для вычисления математического ожидания функции связности M [ и 2 ] необходимо выполнить статистическое усреднение стохастического дифференциального уравнения (33)
dM [ u2 ] = M [ ( A + B - и 2 ) - ( 1 - u2 • ) ]•
dc
1 - C 2
Исключение из уравнений (25) и (29) вспомогательной переменной го приводит к стохастическому дифференциальному уравнению диффузии Ито относительно объемного содержания второго компонента c
du2 =
( A + B - и 2) -
dc
1 - C 2
+ о- и2
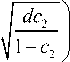
- ( 1 - и 2 ) .
Стохастическое дифференциальное уравнение (27) с начальным условием (26) решается численно с помо-
и получить уравнение, содержащее статистические моменты dM [ и2 ] 1
--- —- =---х dc2 1 - c2
х ( A + B - M [ u2 ] - A - M [ u2 • ]- B - M [ U - - + 1 ] ) . (35)
Рекуррентное вычисление с помощью уравнения (35) статистических моментов вида M [ и2 ] приводит к появлению моментов все более высоких порядков, образующих бесконечную цепочку статистических уравнений, которую можно оборвать, сделав определенные допущения.
В качестве такого допущения здесь предполагается, что флуктуации величины и2 = и 2 ( c 2) относительно ее
математического ожидания M [ и2 ] пропорциональны случайной величине 8 = 8 ( е 2)
и2 -M[и2] = ^-8 .
траекторий функции связности и 2 ( е 2) и кривая ее математического ожидания M [ и 2 ] , построенная в соответствии с численным решением задачи Коши (39), (40).
Здесь ^ = a- M [ и 2 ] - ( 1 - M [ и2 ]2 ) пропорциональности.
Тогда выражение для величины мулы (36), принимает вид
–
коэффициент
u h , с учетом фор-
u h = M [ и , ] h -1 1 + ? ,
2 L2J I M [ и 2 ]
. h
*8
.
Ограничиваясь в формуле (37) малыми флуктуаци-
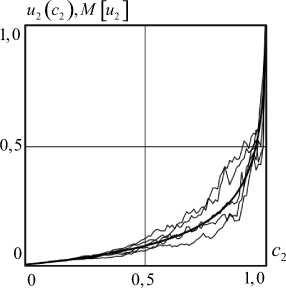
Рис. 2. Семейство стохастических траекторий функции связности и 2 ( е 2 ) , построенных в соответствии с численными реализациями алгоритма (34) и кривая математического ожидания M [ и 2 ] , построенная по результатам численного решения задачи Коши (39), (40)
ями
4т£ м [ и 2 ]
< 1, рассмотрим три слагаемых сходяще-
гося биномиального ряда
и2 = M [ u 2 ] h х
х 1 + h -
^
M [ и2 ]
- 8+ h3hzA
M [ и 2 ] 2
-8 2 +••• . (38)
Вычисляя по формуле (38) средние величины
M [ и } ]. M [ и 2 ]*( 1 .-3L 2
( 2 M [ и 2 ]
м [ и 2-+ 1 ] « м [ и 2 ]2+ 1 - f 1 + Miz 1 L - 8 2
I 2 м [ и 2 ] J
[ПW1]
и подставляя их в уравнение (35), находим дифференциальное уравнение для математического ожидания
M [ и 2 ] функции связности и 2 ( е2 )
dM [ и 2 ] 1 - M [ и 2 ]2
dc 2
1 — С2
- ( A + B - M [ и 2 ]) —
2-a 2 —
12 ( 1 — " [ и ^
- M [ и 2 ] ------------ —х
х ( A - ( 2 — 1 ) + B - ( 2 + 1 ) - M [ и 2 ]) . (39)
Начальное условие для уравнения (39) имеет вид
M [ и 2 ( 0 ) ] = 0.
Сравнение результатов численного решения задач Коши (39), (40) с численными значениями статистического среднего, вычисленного по всем m = 50 реализациям алгоритма (34), показывает их почти полное совпадение.
На рис. 2 представлены численные реализации решений алгоритма (34) в виде семейства стохастических
Fig. 2. The family of stochastic trajectories of the connection function и2 (е2) constructed in accordance with the numerical implementations of the algorithm (34) and the mathematical expectation curve M [и2 ] constructed from the results of the numerical solution of the Cauchy problem (39), (40)
Расчетные значения: A = 0,1; B = 0,5 ; n = 100; m = 50; a = 0,5 ; 2 = 1.
Эффективные стохастические модули упругости композиционного материала рассчитываются по формулам (23), (34) и (39), (40).
На рис. 3 представлены численные реализации расчетов стохастических модулей упругости ц * в виде семейства стохастических траекторий, построенных с помощью алгоритма (28), и кривая математического ожидания стохастического модуля упругости M [ц^ ] , построенная в соответствии с численным решением задачи Коши (39), (40). Все стохастические траектории модуля ц * и его математическое ожидание M [ц * ] расположены внутри вилки верхней и нижней границ Хашина – Штрикмана.
Расчетные значения: A = 0,1; B = 0,5 ; n = 100; m = 50; a = 0,5 ; 2 = 1; ц = 1; v = 0,35 ; ц2 = 20; v2 = 0,25.
Применим полученные результаты для расчета модулей упругости композиционного материала, образованного из кобальта ( Co ) , упрочненного дисперсными частицами карбида вольфрама ( WC ) .
В работе [37] представлены экспериментальные данные по измерению эффективного модуля упругости Юнга двухкомпонентного композиционного материала
( Co - WC ) . Значения [ПW2] модуля упругости и коэффициента Пуассона первого компонента – кобальта – составляют E = 206,27 ГПа и Vj = 0,30 . Значения модуля упругости и коэффициента Пуассона второго компонента – карбида вольфрама составляют E2 = 703,18 ГПа и v2 = 0,22.
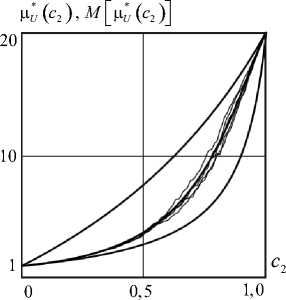
Рис. 3. Семейство стохастических траекторий функции модуля упругости Цу (с2), построенных с помощью алгоритма (34), кривая математического ожидания стохастического модуля упругости M ^цу (c)] , построенная в соответствии с численным решением задачи Коши (39), (40), и верхняя и нижняя границы Хашина – Штрикмана
-
Fig. 3. The family of stochastic trajectories of the elastic modulus function ц у ( c 2) constructed using algorithm (34), the
mathematical expectation curve of the stochastic elastic modulus M ^ц у ( c 2 ) J , constructed in accordance with the numerical solution of the Cauchy problem (39), (40), and the upper and lower Khashin – Shtrikman bounds
На рис. 4. представлено сравнение численных реализаций расчетов стохастических модулей упругости *
EU в виде семейства стохастических траекторий, построенных с помощью формул (23) и алгоритма (34).
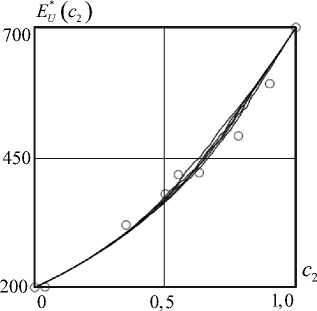
Рис. 4. Семейство стохастических траекторий функции модуля упругости E U ( c 2 ) , построенных с помощью формул (23) и алгоритма (34). Светлыми кружками обозначены экспериментальные значения модуля упругости Юнга композита
-
Fig. 4. A family of stochastic trajectories of the elastic modulus function constructed E у ( c 2) using formulas (23) and algorithm (34). The open circles indicate the experimental values of the Young's modulus of elasticity of the composite
Расчетные значения: A = 0,2; B = 1,0 ; n = 100; m = 50; a = 1,0 ; X = 1.
В работе [38] представлены экспериментальные данные по измерению эффективного модуля упругости Юнга еще одного двухкомпонентного композиционного материала ( Co - WC ) . В этом случае значения модуля упругости и коэффициента Пуассона первого компонента - кобальта - составляют E = 207,93 ГПа и Vj = 0,31. Значения модуля упругости и коэффициента Пуассона второго компонента – карбида вольфрама – составляют Вг = 710,08 ГПа и v2 = 0,19 .
На рис. 5. представлено сравнение численных реализаций расчетов стохастических модулей упругости *
E такого композиционного материала в виде семейства стохастических траекторий, построенных с помощью формул (23) и алгоритма (34).
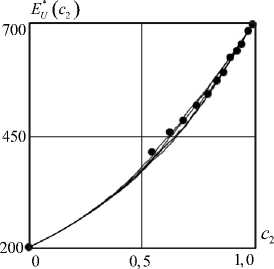
Рис. 5. Семейство стохастических траекторий функции модуля упругости E U ( c 2 ) , построенных с помощью формул (23) и алгоритма (34). Точками обозначены экспериментальные значения модуля упругости Юнга композита
-
Fig. 5. A family of stochastic trajectories of the elastic modulus function constructed E U ( c 2 ) using formulas (23) and algorithm (34). The dots indicate the experimental values of the Young's modulus of elasticity of the composite
Расчетные значения: A = 0,25 ; B = 0,25 ; n = 100; m = 50; a = 1,00 ; X = 1.
Заключение
Предложена новая математическая модель расчета эффективных модулей упругости микронеоднородного двухкомпонентного изотропного композиционного материала, связность компонентов которого изменяется случайным образом в зависимости от уровня их относительных объемных содержаний.
Сформулировано стохастическое уравнение для параметра связности составляющих компонентов, согласно которому при увеличении объемного содержания наполнителя отдельные включения образуют структуры матричной смеси в виде взаимопроникающих каркасов, а затем превращаются в новую связующую матрицу с отдельными включениями из материала остатков старой матрицы.
В соответствии с методом Эйлера – Маруямы построен алгоритм численного решения этого стохастического дифференциального уравнения. Каждой реализации этого алгоритма соответствует своя стохастическая траектория случайной функции связности составляющих компонентов композиционного материала.
Разработан вариант метода вычисления математического ожидания случайной функции связности составляющих компонентов и получено для него соответ- ствующие дифференциальное уравнение. Показано, что численное решение этого уравнения и среднее значение функции фактора производства, вычисленное по всему ансамблю стохастических траекторий, дают близкие численные значения.
Список литературы К теории упругости микронеоднородных сред, учитывающей стохастические изменения связности составляющих компонентов
- Эшелби Дж. Континуальная теория дислокаций. - М.: Иностранная литература, 1963. - 248 с.
- Hashin Z. Theory of mechanical behavior of heterogeneous media // Appl. Mech. Rev. - 1964. - Vol. 17, no. 1. - P. 1-10.
- Hill R. A self-consistent mechanics of composite materials // J. Mech. Phys. Solids. - 1965. - Vol. 13, no. 4. - P. 213-222.
- Хорошун Л.П. О методе определения упругих модулей армированных тел // Механика полимеров. - 1968. - № 1. -С. 78-87.
- Yeh R.H.T. Variational principles of the elastic moduli of composite materials // J. Appl. Phys. - 1970. - Vol. 41, no. 8. -P. 3353-3356. DOI: 10.1063/1.1659424
- Шермергор Т.Д. Теория упругости микронеоднородных сред. - М.: Наука, 1977. - 400 с.
- Композиционные материалы: 8 т. Т. 2. Механика композиционных материалов / под ред. Дж. Сендецки. - М.: Мир, 1978. - 568 с.
- Кристенсен Р. Введение в механику композитов. - М.: Мир, 1982. - 336 с.
- Ванин Г.А. Микромеханика композиционных материалов. - Киев: Наукова думка, 1985. - 304 с.
- Сараев Л.А. Математическое моделирование упруго-пластических свойств многокомпонентных композиционных материалов. - Самара: АНО СНЦ, 2017. - 222 с.
- Алешин В.И. Эффективные упругие свойства двухфазных композитов // Журнал технической физики. - 2007. -Т. 77, № 9. - С. 54-60.
- Ustinov K.B., Goldstein R.V. On application of classical Eshelby approach to calculating effective elastic moduli of dispersed composites // Int. J. Fract. - 2007. - Vol. 147, no. 1-4. -P. 55-66.
- Zheng Q.-S., Du D.-X. An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution // J. Mech. Phys. Solids. - 2001. - Vol. 49, no. 11. - P. 2765-2788.
- Большаков В.И., Андрианов И.В., Данишевский В.В. Асимптотические методы расчета композитных материалов с учетом внутренней структуры. - Днепропетровск: Пороги, 2008. - 247 с.
- Димитриенко Ю.И., Соколов А.П. Об упругих свойствах композиционных материалов // Математическое моделирование. - 2009. - Т. 21, № 4. - С. 96-110.
- Рогачев Е.А., Зверев М.А., Суриков В.И. Прогнозирование упругих свойств полимерных композиционных материалов // Омский научный вестник. Серия: Приборы, машины и технологии. - 2010. - № 3 (93). - С. 28-31.
- Димитриенко Ю.И., Соколов А.П. Многомасштабное моделирование упругих композиционных материалов // Математическое моделирование. - 2012. - Т. 24, № 5. - С. 3-20.
- Abedini A., Chen Z.T. A micromechanical model of particle-reinforced metal matrix composites considering particle size and damage // Computational Materials Science. - 2014. -Vol. 85. - P. 200-205. DOI: 10.1016/i.commatsci.2014.01.012
- Dominguez-Rodriguez G., Tapia A., Aviles F. An assessment of finite element analysis to predict the elastic modulus and Poisson's ratio of singlewall carbon nanotubes // Computational Materials Science. - 2014. - Vol. 82. - P. 257-263. DOI: 10.1016/j.commatsci.2013.10.003
- Головин Н.Н., Зарубин В.С., Кувыркин Г.Н. Оценка эффективных упругих характеристик материалов, модифицированных фуллереном // Композиты и наноструктуры. -2011. - № 4. - С. 21-31.
- Моделирование зависимостей физико-механических характеристик от параметров микро- и наноструктуры полимерных композиционных материалов / С.А. Лурье, Ю.М. Миронов, В.А. Нелюб, А.С. Бородулин, И.В. Чуднов, И.А. Буянов, Ю.О. Соляев // Наука и образование: научное издание МГТУ им. Н.Э. Баумана. - 2012. - № 6. - С. 38-60. DOI: 10.7463/0612.0431339
- Modelling of mechanical properties of nanoparticle-filled polyethylene / В. Lehmann, A.K. Schlarb, K. Friedrich, M.Q. Zhang, M.Z. Rong // Int. J. Polym. Mater. - 2008. - Vol. 57, no. 1. - P. 81-100.
- Bulk Nanostructured Materials: Non-Mechanical Synthesis / Y. Ivanisenko, A. Darbandi, S. Dasgupta, R. Kruk, H. Hahn // Advanced Engineering Materials. - 2010. - Vol. 12, no. 8. - P. 666-676. DOI: 10.1002/adem.201000131
- Лурье С.А., Соляев Ю.О. Модифицированный метод Эшелби в задаче определения эффективных свойств со сферическими микро-и нановключениями // Вестник
- Пермского государственного технического университета. Механика. - 2010. - № 1. - С. 80-90.
- Зайцев А.В., Фукалов А.А. Эффективные модули объемного сжатия дисперсноупрочненных композитов со сплошными и полыми анизотропными сферическими включениями // Вестник Пермского государственного технического университета. Механика. - 2010. - № 4. -С. 46-54.
- Study of Reinforcing Mechanisms in TRIP-Matrix Composites under Compressive Loading by Means of Micromechanical Simulations / S. Priiger, L. Mehlhorn, U. Muhlich, M. Kuna // Advanced Engineering Materials. - 2013. - Vol. 15, no. 7. -P. 542-549. DOI: 10.1002/adem.201200323
- Влияние физикомеханических характеристик полых стеклянных микросфер на свойства сферопластиков / И.И. Соколов, М.Г. Долматовский, И.С. Деев, В.Я. Стеценко // Пластические массы. - 2005. - № 7. - С. 16-18.
- Influence of Powder Size on Production Parameters and Properties of Syntactic Invar Foams Produced by Means of Metal Powder Injection Moulding / J. Weisel, N. Salk, U. Jehring, J. Baumeister, D. Lehmhus, M.A. Bayoumi // Advanced Engineering Materials. - 2013. -Vol. 15, no. 3. - P. 118-122. DOI: 10.1002/adem.201200129
- Jin H.-J., Weissmuller J. Bulk Nanoporous Metal for Actuation // Advanced Engineering Materials. - 2010. - Vol. 12, no. 8. - P. 714-723. DOI: 10.1002/adem.200900329
- Schmidt K., Becker J. Generating Validated 3D Models of Microporous Ceramics // Advanced Engineering Materials. - 2013. -Vol. 15, no. 1-2. - P. 40-45. DOI: 10.1002/adem.201200097
- Giraud A., Sevostianov I. Micromechanical modeling of the effective elastic properties of oolitic limestone // Int. J. Rock Mech. Min. - 2013. - Vol. 62. - P. 23-27.
- Effect of Pore Morphology on Deformation Behaviors in Porous Al by FEM Simulations / Y.J. Cho, W.J. Wook Jin Lee,
- Deqing W. Relation of Cell Uniformity and Mechanical Property of a Close Cell Aluminum Foam // Advanced Engineering Materials. - 2013. - Vol. 15, no. 3. - P. 175- 179. DOI: 10.1002/adem.201200135
- Montero-Chacon F., Marin-Montin J., Medina F. Meso-mechanical characterization of porosity in cementitious composites by means of a voxel-based finite element model // Computational Materials Science. - 2014. - Vol. 90. - P. 157-170. DOI: 10.1016/i.commatsci.2014.03.066
- Functionalized Metallic Hollow Sphere Structures / H. Goehler, U. Jehring, J. Meinert, R. Hauser, P. Quadbeck, K. Kuemmel, G. Stephani, B. Kieback // Advanced Engineering Materials. - 2014. - Vol. 16, no. 3. - P. 335-339. DOI: 10.1002/adem.201300057
- Rapid Sintering of Porous Monoliths Assembled from Microbeads with High Specific Surface Area and Multimodal Porosity / Th.C. Schumacher, T.Y. Klein, L. Treccani, K. Rezwan // Advanced Engineering Materials. - 2014. - Vol. 16, no. 2. -P. 151-155. DOI: 10.1002/adem.201300220
- Nishimatsu C., Gurland J. Experimental servey of the deformation of the hardductile two-phase alloy system W-Co // Trans. Amer. Soc. Metals. - 1960. - Vol. 52, No. 2. -P. 469-484.
- A systematic investigation of elastic moduli of W-Co alloys / H. Doi, Y. Fujiwara, K. Miyake, Y. Oosawa // Met. Trans. -1970. - Vol. 1, no. 5. - P. 1417-1425.
- Современные композиционные материалы / под ред. Л.И. Браутмана и Р. Крока. - М.: Мир, 1970. - 672 с.
- Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и практика численного решения. - СПб.: Изд-во Политехн. ун-та, - 2007. - 800 с.


