К термодинамике процессов восстановления оксидов железа в атмосфере водяного газа

Процессы восстановления оксидов металлов газообразными и твердыми восстановителями лежат в основе всех металлургических технологий. Актуальность проблемы требует новых исследований и корректировки в трактовке известных результатов теоретических и прикладных работ.

Термодинамический анализ процессов восстановления оксидов железа в бинарных газовых фазах (Н 2 – Н 2 О) и (СО – СО 2 ) может быть выполнен с достаточной точностью на основании уточненных справочных данных [1] для следующих реакций:

3Fe₂O₃ + CO = 2Fe₃O₄ + CO₂,

A r G T (1) = - 79 994 - 34,325 T In T + 226,305 T , Дж;

3Fe O +H =2Fe O +H O,

A r G T (2) = - 43 594 - 34,325 T In T + 192,82 T , Дж;

Fe O +CO=3FeO+CO ,

• 34                 2(3)

A r G T (3) = - 10 034 - 38,635 T In T + 271,78 T , Дж;

14Fe 3 O 4 +CO=34Fe α +CO 2 ,

• 34 α 2(3*)

A r G T (3 * ) = - 18 844 - 9,66 T In T + 86,695 T , Дж;

Fe O +H =3FeO+H O,

• 34 2           2(4)

A r G T (4) = 26 546 - 38,635 T In T + 238,315 T , Дж;

14Fe 3 O 4 +H 2 =34Fe α +H 2 O,

(4*)

A r G° T (4 * ) = 17 736 - 9,66 T In T + 53,23 T , Дж;

FeO +CO=Feα +CO2,

A r G T (5) = - 21785 + 25 T , Дж, T <  1185 K;

FeO + CO = Feγ + CO2,

A r G T (6) = - 21484 + 24,75 T , Дж, T = 1185 ^ 1650 K;

FeO+H2 =Feα + H2O,

A r G T (7) = 14 799 - 8,465 T , Дж, T <  1185 K;

FeO+H2 =Feγ + H2O,

A r G T (8) = 15 096 - 8,715 T , Дж, T = 1185 ^ 1650 K;

Хорошо известная графическая интерпретация параметров равновесия двухфазных смесей твердых оксидов (Fe 2 O 3 , Fe 3 O 4 ), (Fe 3 O 4 , FeO), оксидов с железом (Fe₃O₄, Fe) и (FeO, Fe) с газовыми смесями водорода и паров воды в координатах x H 2 - T не требует какой-либо корректировки. С аналогичной диаграммой фазовых равновесий, реализующихся при восстановлении оксидов железа в газовой смеси (СО – СО 2 ), ситуация сложнее. При расчетах параметров равновесия необходимо кроме реакций восстановления учитывать реакцию Белла – Будуара, то есть конверсию СО с образованием сажистого углерода и СО 2 :

2CO = CO 2 + C.                         (9)

Рассчитанная диаграмма фазовых равновесий представлена на рис. 1. Линии a ′ a , aa ′′ , aa ′′′ определяют параметры равновесий, реализующихся при восстановлении оксидов железа монооксидом углерода без учета его конверсии. Линия EF определяет равновесия реакции конверсии. При термодинамическом равновесии состояния, определяемые линиями a ′ a , aС и aD , не должны реализоваться, так как они соответствуют концентрациям СО большим, чем равновесные концентрации для реакции Белла–Будуара.

Однако реакция конверсии при сравнительно низких температурах, до 950 K, сильно заторможена (большая энергия активации), особенно в отсутствии избыточной углеродистой фазы. Поэтому возможна реализация процессов восстановления Fe 3 O 4 до Fe, Fe 3 O 4 до FeO и FeO до Fe в ме-тастабильном режиме, описываемом кривыми a ′ a , a a ′′ , a a ′′′ . В соответствии с таким допущением практически во всех монографиях диаграмма фазовых равновесий восстановления оксидов железа в смеси (СО – СО 2 ) представляется без кривой Белла–Будуара.

В реальных технологиях восстановление оксидов железа реализуется в сложных газовых смесях, содержащих и СО, и Н2. Равновесные параметры таких систем можно представить в виде громоздких таблиц, а графическая интерпретация их отсутствует. Общепринятая практика наложения диаграмм фазовых равновесий систем «оксиды железа – Н2– Н2О» и «оксиды железа – СО – СО2» (рис. 2) малоинформативна. Из этого рисунка следует лишь, что при температуре 1093 K равновесные газовые фазы характеризуются равенством xCO xCO2 = xH 2 xH2O , которое выполняется при разных составах газовой смеси. Каковы же эти составы и каковы составы равновесных газовых фаз при других температурах по рис. 2 определить нельзя. Кроме того, на основании такого графика делаются выводы о восстановительных способно- стях СО и Н2: при температурах ниже 1093 K (820 °С) «лучшим» восстановителем предлагается считать монооксид углерода, а при температурах выше 1093 K – водород. На самом деле такое сравнение следует проводить на основании результатов расчетов равновесия систем «оксиды железа – водяной газ».

Вычисленные нами параметры равновесия таких систем в предположении отсутствия реакции конверсии СО следует представлять объемной трехмерной диаграммой (рис. 3). На этой пространственной диаграмме следует выделить две перпендикулярные плоскости T - x H 2 и T - x CO , на которых изображены хорошо известные «вилки», линии которых определяют составы бинарных газовых смесей в системах:

• – линии a ′ a , aa ′′ и aa ′′′ характеризуют системы «Fe 3 O 4 – Fe α – СО – СО 2 », «Fe 3 O 4 –FeO– СО – СО 2 » и «FeO–Fe α (Fe γ ) – СО – СО 2 »;

  – линии b ′ b , bb ′′ и bb ′′′ характеризуют системы «Fe 3 O 4 –Fe α – Н 2 – Н 2 О», «Fe 3 O 4 –FeO– Н 2 – Н 2 О» и «FeO–Fe α (Fe γ ) – Н 2 – Н 2 О».

Как видно, точки пересечения кривых aa ′′ и bb ′′ , кривых aa ′′′ и bb ′′′ виртуальны, поэтому температуру 1093 K (см. рис. 2) как рубежную, позволяющую сравнивать восстановительные способности водорода и монооксида углерода, следует интерпретировать иначе.

Возможные составы равновесного с оксидами железа водяного газа определяются координатами множества точек на поверхностях:

– поверхности b ′ baa ′ для системы «Fe 3 O 4 – Fe α – СО – СО 2 – Н 2 – Н 2 О»;

– поверхности bb ′′ a ′′ a для системы «Fe 3 O 4 – FeO– СО – СО 2 – Н 2 – Н 2 О»;

– поверхности bb ′′′ a ′′′ a для системы «FeO– Fe α (Fe γ ) – СО – СО 2 – Н 2 – Н 2 О».

Образующие этих поверхностей, получающиеся сечением изотермической плоскостью, представ-

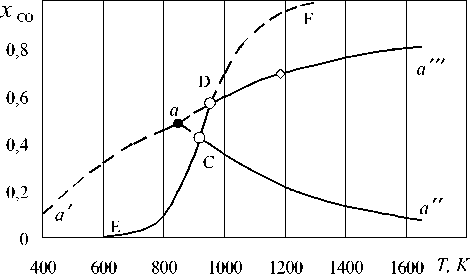
Рис. 1. Параметры равновесия в системе «оксиды железа – СО – СО 2 »

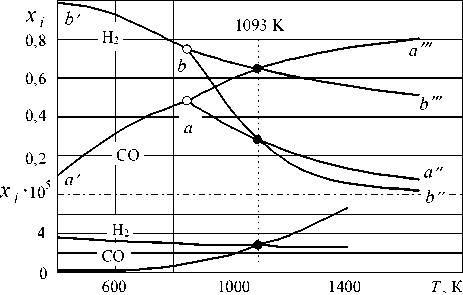
Рис. 2. Диаграмма фазовых равновесий при восстановлении оксидов железа газами СО и Н 2 , построенная методом наложения: a, b – точки четырехфазных равновесий (850 K); точки • – «пересечения» кривых (1093 K); штрихпунктирная линия означает смену масштаба для ^CO и x _{H 2}

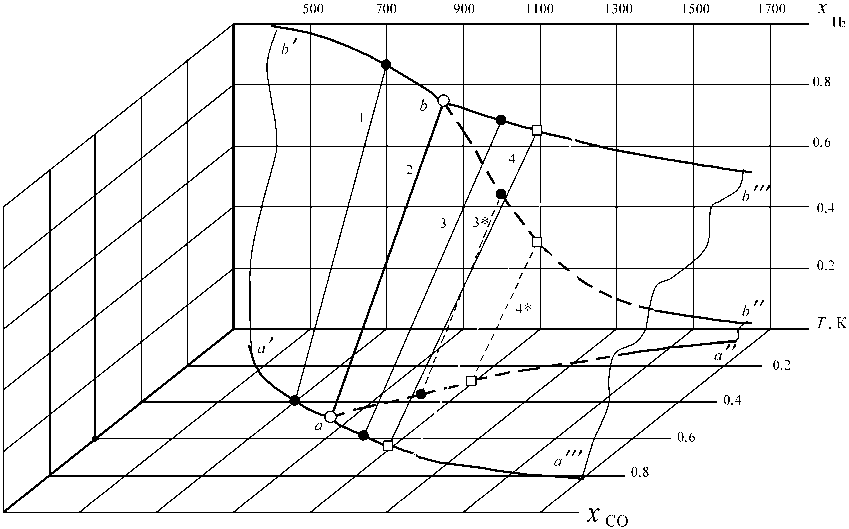
Рис. 3. Диаграмма фазовых равновесий оксидов железа с водяным газом: поверхности: a'abb' -система «Fe 3 O 4 + Fe a — СО - СО 2 - Н - Н 2 О», aa"b"b - система «Fe 3 O 4 + FeO - СО - СО 2 -Н 2 - Н 2 О», aa"'b^mb - система «FeO + Fe a ( Fe _Y ) - СО - СО 2 - Н - Н 2 О; изотермы: 1 - 700; 2 - 850; 3 и 3* – 1000; 4 и 4* – 1093 K

ляют собой изотермические прямые линии. Для доказательства этого приведем здесь результаты конкретных расчетов.

Возьмем для примера восстановление Fe 3 O 4 до FeO при температурах 850, 1000 K и FeO до Fe при температуре 1000 K. Если избыточное количество оксида Fe₃O₄ (или FeO) поместить при заданной температуре в герметичный реактор с газовой смесью (Н 2 + СО) разного состава, определяемого величиной

дует рассчитать равновесие двух независимых реакций (3) и (4), то есть решить систему четырех уравнений с четырьмя неизвестными:

^x CO 2

3 = xCO

^x H 2 O

4 = xH2

C =

ⁿ H 2

n

CO исх

TH²-к x CO )

, исх

и учесть, что в рассматриваемых системах в результате реакций восстановления не изменяются

количества атомов водорода и углерода, то не из-

меняется и соотношение между ними:

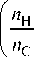
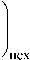
2 n

H ₂

n

CO исх

x H₂O ⁺ x H₂

^x C О ^{+ x} CO 9 .

2 равн

= 2C =

= С .

^x H₂ ^{+ x} H₂O ^x CO ^{+ x} CO₂

Z xt= 1.

Термодинамические характеристики реакции во-

дяного газа в расчетах не используем, так как она не является независимой и получается вычитанием реакции (3) из реакции (4):

H₂ + CO₂ =H₂O + CO,

A r G °T (5) = 3 6 5 80 - 3 3,465 T , Дж;         (12)

' ² n H₂O ^{+ 2 n} H₂ '

. n CO ⁺ n _C o₂ .

2   равн

Согласующиеся результаты получаются, если расчетах задаваться величиной:

K 850 = 0,316, K 1000 = 0,688.

Параметры равновесия этой реакции можно использовать для проверки правильности расчетов.

Для определения равновесных параметров другой системы «FeO–Fe– СО – СО 2 – Н 2 – Н 2 О» рассчитываем равновесие реакций (5) и (7). Решаем такую систему четырех уравнений с четырьмя неизвестными:

в

nO к n H2O)

E =

^x CO ^{+ x} CO₂

[9 ⁺ x H9O J ²²равн

или другим концентрационным параметром.

Для определения равновесных параметров системы «Fe3O4–FeO– СО – СО2– Н2– Н2О» сле-

^x CO₂

⁵ = * x CO

x H 2 O

7 = *

x H 2

x H2 + xH2O x C O + xC O2

Z x * = 1.

Системы уравнений (11) и (13) формально

одинаковы и имеют однотипные решения:

Xc D —,

CO ( C + 1)( K 3 + 1)

x —

CO²    ( C + 1)( K 3 + 1),

C X"H,

H²    ( C + 1)( K 4 + 1)

— xH2O   (C +1)( k4 +1).

v * -1

Xc о —

CO ( C + 1)( K 5 + 1)

„* _

XcD — ,

CO²    ( C + 1)( K 5 + 1)

„ *

Х и —,

H² ( C + 1)( K 7 + 1)

*

x-pj r) —.

H²O    ( C + 1)( K 7 + 1)

Здесь x i – равновесные концентрации компонентов водяного газа, равновесного со смесью «Fe 3 O 4 –FeO»,

x * - со смесью «FeO-Fe».

Во-первых, из этих уравнений следует:

x H 2	C ( K 3 + 1)	_ C ( K 3 + 1)	(16)
—		x H 1 —            x cO;
x CO	( K 4 + 1)	H2     ( K 4 + 1) CO
* x H2	— C ( K 5 + 1)	*     C ( K 5 + 1) *	(17)
* x CO	( K 7 + 1) ,	x "h —             x^ . H 2     ( K 7 + 1) CO

Таким образом, между концентрациями водорода

и монооксида углерода в равновесном с оксидами железа водяном газе при заданной температуре и при заданном концентрационном параметре С имеют место линейные зависимости, эти зависимости представлены на рис. 4 линиями 1 ( a'b' ) и

2 ( a"b" ).

Во-вторых, результаты расчетов по уравнениям (14) и (15) для температур 1000 и 850 K и разных С представлены в таблице и на рис. 4 и 5. Легко проверить, что любые xi для заданной тем- пературы и заданной величины С соответствуют константе равновесия реакции водяного газа (12), например:

при Т = 850 K и С = 0,5:

^K 5(850) ^—

0,085 • 0,321

0,345 • 0,249

— 0,317;

при Т = 1000 K и С = 3:

^K 5(1000) ^—

°,⁴²⁰⁰,⁰⁸⁸ — 0,688, 0,162 • 0,331

K ₅(looo) — ^0,238 ^ ^0,149 — 0,686 .

^5(1000) 0,101 . 0,5 1 2

Наконец, в-третьих, линейность изотермических линий можно подтвердить следующим образом. Представленные пространственная диаграмма и ее изотермические сечения (рис. 3–6) определяют параметры равновесного водяного газа. Термо- динамические характеристики этой реакции не зависят от природы конденсированных фаз, с которыми находится в равновесии водяной газ. равновесия реакции (12)

^x CO ^x CO₂

^x H 2 ^x H 2 O

Представим константу следующим образом:

^x CO ^x H₂O

K12 —          — xH2 xCO2

Концентрации компонентов газовой смеси, равновесной с «Fe 3 O 4 -FeO-Fe», «Fe 3 0 4 -FeO» и «FeO-Fe» ’

С	x i	Т , K
		850	1000	1000 *
0,25	СО	0,385	0,280	0,476
	СО 2	0,415	0,520	0,324
	H 2	0,149	0,088	0,136
	H 2 O	0,051	0,112	0,064
0,50	СО	0,321	0,234	0,397
	СО 2	0,345	0,432	0,270
	H 2	0,249	0,147	0,227
	H 2 O	0,085	0,187	0,106
0,75	СО	0,275	0,200	0,340
	СО 2	0,296	0,372	0,231
	H 2	0,320	0,188	0,292
	H 2 O	0,109	0,240	0,137
1,0	СО	0,241	0,175	0,298
	СО 2	0,259	0,325	0,202
	H 2	0,373	0,220	0,341
	H 2 O	0,127	0,280	0,159
2,0	СО	0,160	0,117	0,199
	СО 2	0,173	0,217	0,135
	H 2	0,497	0,293	0,455
	H 2 O	0,170	0,373	0,211
С = 3,0	СО	0.120	0,088	0,149
	СО 2	0,130	0,162	0,101
	H 2	0,559	0,331	0,512
	H 2 O	0,191	0,419	0,238
С = 4,0	СО	0,096	0,070	0,119
	СО 2	0,104	0,130	0,081
	H 2	0,597	0,352	0,545
	H 2 O	0,203	0,448	0,255

Из этого уравнения следует, что соотношение между x CO x CO 2 и x H 2 x H 2 O является функцией только температуры. Числители в этих отношениях определяются координатами любой точки на изотермах, например точками A , A ‘ и A " на рис. 6. Для определения величин знаменателей в этих отношениях необходимо провести две дополнительные линии ad и cb и еще по две дополнительные линии через точки A , A ‘ и A" - ng и mf, n'g ' и mf ' n"g” и m "f ". Тогда координаты точек f, f’ и f ' определяют сумму ( x CO + x C _O 2 ), а отрезки fA , f ’A' и f " A " - концентрации x C _O 2 ; координаты точек g , g' и g" определяют сумму ( x _H 2 + x _H 2 _O ), а отрезки gA , g'A' и g" A" - концентрации x _H 2 _O . Из сообра-

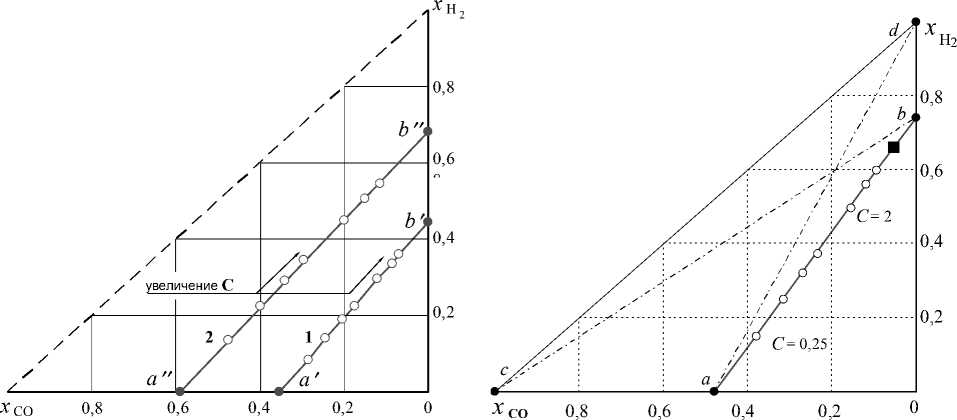
Рис. 5. Равновесные концентрации Н 2 и СО в газовой фазе при 850 K: ab — система «Fe 3 O 4 – FeО – Fe – СО – СО 2 – Н 2 – Н 2 О» (точки ○ — разные С ); точка ■ — система «Fe 3 O 4 – FeО – Fe – СО – СО 2 – Н 2 – Н 2 О – С»

Рис. 4. Равновесные концентрации Н 2 и СО в газовой фазе при 1000 K: 1 – система «Fe 3 O 4 – FeО – СО – СО 2 – Н₂ – Н₂О»; 2 – система«FeO – Fe – СО – СО₂ – Н₂ – Н₂О»; точки ○ – разные С

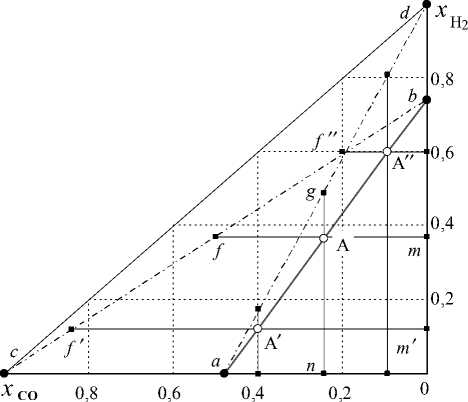
Рис. 6. Демонстрация графического метода определения по изотерме ab (850 K) возможных концентраций компонентов водяного газа в равновесной системе «Fe 3 O 4 – FeO – Fe α – СО – СО 2 – Н 2 – Н 2 О»

жений геометрии на основании рис. 6 можно пока- зать, что

Am/ Af = A′m′IA′f′ = A′′m′′/A′′f′′=K

An/ Ag     A ′ n ′ A ′ g ′      A ′′ n ′′/ _{A ′′ g ′′} = K ₁₂

Кроме того, можно показать:

Af =A′′f′′ =A′f′ =K

Am     A ′′ m ′′      A ′ m ′      3 ,

Ag     A′g′ A′′g′′

==   = K ₄ ,

An   A n  A n где K3 и K4 – константы равновесия реакций восстановления (3) и (4).

Таким образом, разными способами доказывается линейность изотермических сечений пространственной диаграммы фазовых равновесий системы ««оксиды железа – СО – СО 2 – Н 2 – Н 2 О».

Изотермические линии соединяют точки, координаты которых определяют равновесные концен- трации xC∗ O для системы «оксиды железа – СО – СО2» (точки a и a′) и равновесные концентрации xH∗ 2 системы «оксиды железа – Н2 – Н2О» (точки b и b′). Это обстоятельство позволяет рассчитывать концентрации компонентов водяного газа, равновесного с оксидами железа, по формулам:

∗ xCO =xCO - xH2

∗

∗ xH2=xH2-∗ xCO, xCO(18)

xH+xHO=1-xCO, xCO +xCO =1-

2 _x H₂ 2

которые получаются из уравнений прямых линий, соединяющих точки a и b , a и d , b и c (см. рис. 6). Таким образом, наряду с графическим методом определения состава равновесного водяного газа его можно рассчитывать аналитически по соотношениям (18) на основании информации о равновесии простых систем.

Выводы

• 1.    Параметры фазовых равновесий при восстановлении оксидов железа водородом и монооксидом углерода, совместно присутствующими в газовой фазе, необходимо представлять пространственной диаграммой.

• 2.    При восстановлении оксидов железа смесью (СО + H 2 ) оба газа принимают участие в восстановлении в соответствии с величинами констант равновесий реакций восстановления и реакции водяного газа. Термодинамическое сравнение восстановительных способностей СО и H₂ возможно на основании результатов расчетов равновесных параметров систем «оксиды – СО – СО 2 – Н 2 – Н 2 О» и состава исходной смеси восстановителей (СО + H 2 ).

• 3.    Характерные точки пересечения кривых, полученные в результате наложения диаграмм восстановления оксидов железа водородом и, независимо, монооксидом углерода, на самом деле не несут приписываемого им физического содержания и требуют корректной интерпретации.

• 4.    В предположении заторможенности реакции конверсии СО при невысоких давлениях газовой фазы и низких температурах возможно использовать для определения равновесных составов водяного газа предложенный графический метод.