К вопросу автоматизированного контроля качества данных геофизических исследований скважин

Введение. Одной из важнейших задач нефтепромысловой геофизики является повышение точности и достоверности количественной интерпретации промыслово-геофизических данных. Решение этой задачи невозможно без достоверных данных геофизических исследований скважин (далее-ГИС) [1].

Первичная обработка и оценка качества полевых данных, оценка материалов производится оператором по исследованию скважин визуально, непосредственно на объекте. Такая оценка требует от оператора значительных познаний в теории геофизических методов исследования скважин, навыков интерпретации ГИС, а также большого опыта работы. Однако большинство операторов, по тем или иным причинам, либо не обладают требуемой квалификацией, либо просто не имеют возможности оценить качество полученных данных вследствие большого объёма проводимых исследований, сложных условий исследования [2], сложных и незнакомых геофизических разрезов скважин и т. д. При выявлении «брака» материала на этапе интерпретации геофизических исследований, требуется повторное проведение исследований, что связано с весьма значительными финансовыми расходами.

В статье «А Hierarchical Approach to Improving Data Quality» [3] присутствует во многом схожая проблематика задачи контроля качества данных. Предлагаемый авторами подход к решению задачи автоматизированного контроля качества геоинформационных данных основан на сопоставлении изображений одной местности, полученных из разных источников. Критерием качества считаются величины взаимных уклонений пар матриц смежности графов, представляющих наборы данных. Подбор и сопоставление изображений выполняется экспертами вручную, являясь при этом актом формализации их опыта, поскольку основная проблема инженерии знаний — это процесс извлечения знаний.

Работа выполнена по тематическому плану Министерства образования и науки РФ № 2.3.13 «Метод сбалансированной дискретизации для задач имитационного моделирования динамических процессов в распределённых объектах».

Постановка задачи. Существует проблема «ранней» оценки качества зарегистрированного материала ГИС, то есть оценки качества в процессе записи и непосредственно после окончания записи. Таким образом, использование автоматических средств обнаружения ошибок и контроля качества регистрируемых данных становится весьма актуальным.

Работа посвящена развитию научных основ, методов и технологий первичного автоматизированного контроля регистрируемых данных при проведении геофизических исследованиях в скважинах. Симптомами ненадёжности фрагментов записи выступают:

• 1)    значения показаний приборов, не имеющие смысла с геолого-геофизической точки зрения, которые могут быть связаны со срывами, выбросами, затяжками, утечками в кабеле, ошибками аналого-цифрового преобразования [4, 5] и т. д.;

• 2)    противоречивые показания приборов, проявляющиеся в расхождениях показаний, полученных различными методами исследования, либо при разных условиях работы одного метода. Например, показания электрических методов на постоянном и переменном токе, либо несоответствие показаний разных зондов при исследовании на постоянном токе;

• 3)    несоответствие показаний приборов априорной информации, имеющейся об объекте исследований. Например, отсутствие артефактов на записи электромагнитных методов при прохождении интервалов перфорации колонны.

Целью автоматизированного контроля качества является выявление вышеуказанных проблемных ситуаций, которые определяют информационную нерегулярность данных и привлечение к ним внимания оператора. Достижение цели обеспечивается обнаружением с некоторой, заранее заданной вероятностью, симптомов проблемных ситуаций в процессе записи данных ГИС, а также непосредственно по завершению исследования.

Скважинные геофизические исследования с математической точки зрения описываются, как функции g=f(h^, где д — измеряемый геофизический параметр, h — глубина. Симптомы нарушения информационной регулярности записей каротажных данных д = f (h} могут быть оп ределены с помощью методов итерационного моделирования неполных данных с использованием многообразий малой размерности [6] для автоматизированного контроля качества данных геофизических исследований.

Алгоритм оценки качества материалов с применением метода моделирования неполных данных. Рассмотрим алгоритм решения задачи оценки качества записи данных ГИС с применением метода восстановления на примере данных метода кажущихся сопротивлений (КС). Скважинные исследования методом КС основаны на расчленении пород, окружающих скважину, по их удельному электрическому сопротивлению (УЭС). При исследованиях методом КС может регистрироваться либо сила тока (токовый каротаж), либо разность потенциалов. В результате каротажа получают токовые диаграммы, характеризующие изменение силы тока по стволу скважины. Исходя из предположения, что большая часть данных не искажена, алгоритм может иметь следующий вид:

• 1.    Из исходного набора данных выбирается окно — окрестность исследуемой точки;

• 2.    Часть данных строки содержащей исследуемую точку удаляется;

• 3.    Проводится восстановление удалённого участка;

• 4.    Восстановленная кривая сравнивается с исходной по критерию минимума среднеквадратических отклонений.

Шаги повторяются для каждой точки исходного набора данных (рис. 1).

Пусть имеется двумерный прямоугольный числовой массив G, строки которого представляют собой функции д = f (А) КС пород скважины, заданные в дискретной форме с одинаковым интервалом и нормированные на диапазон [0...1] независимо друг от друга. Таким образом, каж- дый столбец этой матрицы есть вектор данных а — «изображение» исследуемой среды различными зондами [7-9]. Достоверность каждой точки матрицы G подвергнута сомнению и может быть оценена за счёт скрытых зависимостей между точками её окрестности.

Представим G как одномерный массив векторов а и выберем интервал — окрестность вектора, содержащего исследуемую точку. Таким образом получаем «окно» — матрицу А размера тхп, где т (количество строк) — размерность вектора а, п (количество столбцов) — длина интервала, содержащего окрестность точки. Слева и справа от исследуемой точки, в содержащей её строке, удалим участки данных одинаковой длины, получив, таким образом, версию матрицы А с «пробелами». Применив к матрице с «пробелами» один из методов итерационного моделирования неполных данных восстановим удалённый участок. Контролируемая точка должна находиться строго в центре отбрасываемого участка. Контролируемый участок должен находиться в центре окна, если это возможно. Допускается перестановка местами строк матрицы.

Необходимо также отметить, что хотя количество строк матрицы А и может быть произвольным, для удовлетворительной работы методов восстановления данных требуется не менее трёх строк. Длина интервала подбирается экспериментально для каждого метода ГИС. Эффективный размер интервала для КС составляет от 30 до 50 точек. Длина восстанавливаемого участка должна находиться в пределах 20-50 % от ширины матрицы.

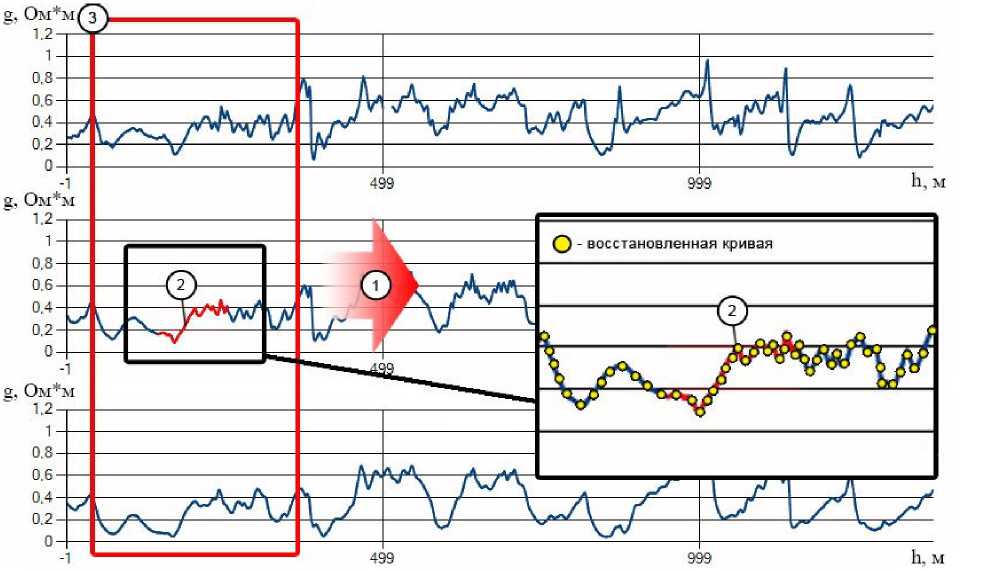
Рис. 1. Иллюстрация алгоритма оценки достоверности данных: 1 — движение скользящего окна; 2 — удалённый участок данных; 3 — скользящее окно

Итерационное моделирование неполных данных с помощью многообразий малой размерности. Рассмотрим три версии метода итерационного моделирования неполных данных с помощью многообразий малой размерности:

• 1.    линейный — с моделированием данных последовательностью линейных многообразий малой размерности;

• 2.    квазилинейный — с построением «главных кривых» (или «главных поверхностей»), однозначно проектируемых на линейные главные компоненты;

• 3.    существенно нелинейный — основанный на построении «главных кривых» с использованием вариационного принципа; итерационная реализация этого метода близка методу самоорганизующихся карт Кохонена.

Все версии метода могут трактоваться как построение нейросетевого конвейера, решающего следующие задачи:

• 1.    заполнение пробелов в данных;

• 2.    ремонт данных, корректировка значений исходных данных так, чтобы наилучшим образом работали построенные модели;

• 3.    построение вычислителя, заполняющего пробелы в поступающей на вход строке данных (в предположении, что данные о новых объектах связаны теми же самыми отношениями, что и в исходной таблице).

Столбец матрицы А есть вектор ack пробелами, который представляется как /с-мерное линейное многообразие 1_а, параллельное к координатным осям, которые соответствуют удалённым данным. При наличии априорных ограничений на пропущенные значения место Ц занимает параллелепипед Р_а сЦ.

Построим моделирующее эти данные линейное многообразие малой размерности следующим образом: за основу возьмём прямую ^х)=ху+Ь, которая задаётся направляющим вектором у и проходит через точку, определяемую вектором Ь. Расположим эту прямую так, чтобы она наилучшим (в некотором точном смысле) образом приближала исходные данные. Если взять в качестве проектора данных на эту прямую ортогональный проектор, то исходный вектор данных а ортогонально проецируется в вектор ^Рг/(а) на полученной прямой (рис. 2).

g/h)

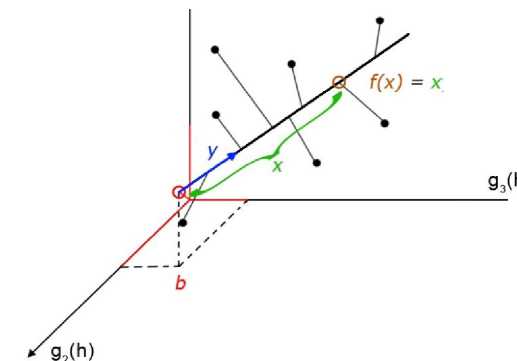
Рис. 2. Моделирующие многообразие малой размерности

Для исходных данных можно посчитать их уклонения от линейной модели, которые находятся из разницы между исходными данными и их проекциями на полученную прямую. Для полученных уклонений также можно построить приближающую наилучшим (в определённом точном смысле) прямую, для которой тоже можно рассчитать уклонения. В результате, получается итерационный процесс моделирования данных, который заключается в том, что для исходных данных строится наилучшая (в определённом точном смысле) модель — линейное многообразие М малой размерности. Далее из данных А вычитаются проекции ^РгДа). Получаем уклонения от первой модели. Для этого множества уклонений снова строится простая модель и т. д., пока все уклонения не станут достаточно близки к нулю.

Пусть задана прямоугольная матрица А=^а^, клетки которой заполнены действительными числами или значком @, означающим отсутствие данных. Требуется представить исходную матрицу А в виде суммы одноранговых матриц Pg-. А = ^, Pq, где каждая Pq имеет вид xjyj + Ь> Сле довательно, ставится задача поиска наилучшего приближения А матрицей вида х^ + bj методом наименьших квадратов:

ф = ЕС^ ^^ ^)2 min-                       (!)

i,j

На первой итерации допускается принять значения вектора /случайным, но нормированным на 1, значения вектора b вычисляются по формуле:

^ьз = ™^{e п},= Е¹-                         (²)

ау*@

Решая задачу (1), для данной матрицы А находим наилучшее приближение матрицей Рх вида xjyj + bj. Далее, из матрицы А вычитаем полученную матрицу Рх, и для полученной матрицы уклонений А-Рх вновь ищем наилучшее приближение Р₂ этого же вида и т. д. Контроль ведётся по остаточной дисперсии столбцов. В результате исходная матрица данных А представляется в виде суммы матриц P_q, т. е. A=Px+P2+...+P_q. Следует обратить особое внимание на то, что центрирование (переход к нулевым средним) к данным с пробелами неприменимо.

С использованием Q полученных факторов можно решать задачи заполнения пропусков в таблице и ремонта искажённых значений:

Q-факторное заполнение пропусков: пропущенные значения в исходной матрице А определяются из суммы Q полученных матриц вида х,у + Ь/,

Q-факторный «ремонт» таблицы: значения в исходной матрице заменяются на сумму Q полученных матриц вида xyj + bj.

При отсутствии пробелов полученные прямые будут ортогональны и мы получим ортогональную систему факторов. Для неполных данных это не так, но возможен процесс ортогонализации полученной системы факторов, который, к примеру, заключается в том, что исходная таблица восстанавливается при помощи полученной системы факторов, после чего эта система пере считывается заново, но уже на дополненных данных.

Для лучшего приближения исходных данных, можно подобрать такую гладкую вектор-функцию, значения переменных которой определяются через проекции данных на уже построенное многообразие, что суммарное значение квадратов уклонений будет минимальным среди всех возможных функций данного класса. Такой тип линий называется квазилинейным

Пусть, как и в случае линейных моделей, задана таблица с пропусками А = (а,]), т. е. некоторые а_ц = @. Построение квазилинейных моделей, наилучшим образом приближающих данные, предлагается проводить в несколько шагов:

• 1.    Построение линейной модели: решение задачи (1). Для определённости полагаем, что (У, 6) = 0, (у, у) = 1.

• 2.    Интерполяция (сглаживание): строится вектор-функция /(f), минимизирующая функционал:

• 3.    Экстраполяция: самая простая экстраполяция полученной вектор-функции f(t) может быть получена при использовании касательных к полученной функции на концах интервала или формул Карлемана.

2       +°°

Ф = Е (^а₀ -№кУ^ *Ц1НЖ              (3)

i,j где а > 0 — параметр сглаживания.

Для решения этой задачи могут быть применены полиномы небольшой степени, кубические сплайны или функция Карлемана [10].

Таким образом, сглаженная вектор-функция f(t) экстраполируется с некоторого конечно го множества {tk} на всю вещественную прямую с использованием формул Карлемана f{t) «ty + b + У/Ж Vtky- b)

2(e^w-e^w‘) (е^м + e^Mk Хе^м + e^Mk)

где А — параметр, характеризующий ширину полосы на плоскости комплексных чисел, где экстраполируемая функция гарантированно голоморфна.

Процедура использования квазилинейных моделей несколько отличается от аналогичной процедуры в линейном случае. Точка на построенной кривой /(f), соответствующая полному вектору данных а строится как Ца, у)). В этом и заключается квазилинейность метода: сначала ищется проекция вектора данных на прямую Pr(a)=/y+f>, t=(a,y), а затем строится точка на кривой f (f). Также и для неполных векторов данных — сначала на прямой ищется ближайшая точка /(а),

Х(е^м + e^Mk )(f - t_k) (е^м + е^Мк Хе^и + е"^к Y

а затем — соответствующая точка на кривой f(f), при f=^a). После построения кривой f(f) из данных вычитаются их проекции, т. е. матрица данных заменяется на матрицу уклонений. Далее снова ищется наилучшее линейное приближение для матрицы уклонений, вновь строится сглаживание, экстраполяция и т. д., пока уклонения не приблизятся в достаточной степени к нулю. Критерием остановки могут выступать остаточные дисперсии.

В результате исходная таблица предстаёт в виде (^факторной модели:

а8^^\ q где аргументом функции служит нормированное скалярное произведение исходного данного на линейную основу квазилинейного многообразия.

Самоорганизующиеся карты Кохонена (Self-Organizing map — SOM) [11] — это модифицированный алгоритм линейного векторного квантования данных, т. е. представления /V точек данных с помощью меньшего числа точек-ядер. Каждое из ядер заменяет собой локальное сгущение данных — таксон. В результате такой замены данные представляются с ошибкой аппроксимации — среднеквадратичного расстояния отточки до ближайшего к ней образца.

Пусть SOM определяется набором точек (ядер) У=\у^ (/) j = 1..т), последовательно расположенных на квадратной сетке. Требуется отобразить на ней набор точек данных X = |%J. Введём преобразование П, которое каждому вектору х еХсопоставляет ближайшую к нему точку из К:

• п                I               1^•

  
  

х )Уд'\У)-х\ ^т|П/ а каждому ядру у„сопоставляется его таксон

К,ЦхеХ {х^^уД.(7)

Минимизируемый функционал, таким образом, будет состоять из следующих слагаемых: o.’ZZk-x.h(8)

ij хеКд

D2 =Zk +Xh -У^Х(9)

• УУ

°з = Е||2у, -у^-у^Д -^УД-Уо-у^-УмЛ ■(

• УУ

Для построения SOM требуется минимизировать функционал:

„ D.           D3

(И)

D — —г + X —у- + ц — у,

X   ш2 т2

где Л, р — параметры связности и нелинейности, «модули упругости».

Пусть метрика является евклидовой. В этом случае функционал D является квадратичным по положениям узлов уд. Это значит, что при заданном разбиении множества точек данных на таксоны для его минимизации потребуется решить систему линейных уравнений размерами pq^pq. Следовательно, эффективным методом минимизации функционала D окажется такой алгоритм:

• 1.    Узлы сетки так или иначе располагаются в пространстве данных.

• 2.    При заданных положениях узлов сетки производится разбиение множества точек данных на таксоны — подмножества К_ц.

• 3.    При заданном разбиении множества точек данных на таксоны производится минимизация функционала D.

Шаги 2 и 3 повторяются до тех пор, пока функционал D не перестанет изменяться (в пределах заданной точности). Процесс сходится, поскольку на каждом этапе минимизации величина D, будет уменьшаться, вместе с тем она ограничена снизу нулём. Более того, процесс сходится за конечное число шагов, поскольку число вариантов разбиения точек данных на таксоны конечно.

Выпишем явно коэффициенты матрицы системы линейных уравнений, которую необходимо решать на каждой итерации алгоритма минимизации. Непосредственное дифференцирование даёт следующие результаты:

^^ — д( ²) у^ ^J + д( V ! д уИ ! д(+1)        ! д(+2) ук+7.,1

2 оу

+ bJ}yk'M + Ь^ук''^ -Ух.

хеКк1

Из уравнения —^=0, /^1...р, /=1...р получим m систем линейных уравнении.

«Вытянем» набор ядер уив один столбец. В результате вектор неизвестных примет вид:

х = кУ1и-.У1ч.Уги-.Угч.-.У^1.-'У^'Ур1

Урд)"

Система уравнений имеет вид Ах=Ь, где s-я компонента вектора свободных членов равна:

£ _ XfcKg

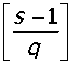
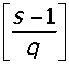
q,

где [...] — операция взятия целой части числа.

'M,i = k,j = l

Ast = ■

а, а', а а', а\

,и) и

,(+1) и и ,(+2) И

= k-l,j = l

ии ''

Ь^М b^J

= k-2,j = /, = k + 2,j = 1, = k,j = / — 2, = kJ = /-1,

где ^

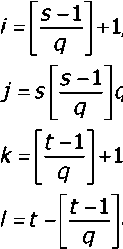
q.

b^\i = k,j = 1 + 2, 0, else,

Матрица, таким образом, имеет девятидиагональный вид.

На протяжении всей работы алгоритма значения элементов матрицы остаются неизменными, изменяются лишь компоненты вектора Ь.

Численные эксперименты показывают высокую эффективность методов итерационного моделирования неполных данных с помощью многообразий малой размерности в задаче заполнения пробелов данных геофизических исследований (рис. 3). Для данных, качество которых не подвергается сомнению, протяжённость удалённого контролируемого участка, успешно восстанавливаемого методом самоорганизующихся карт, составляет до 50 % ширины окна и до 20 % при восстановлении линейным методом.

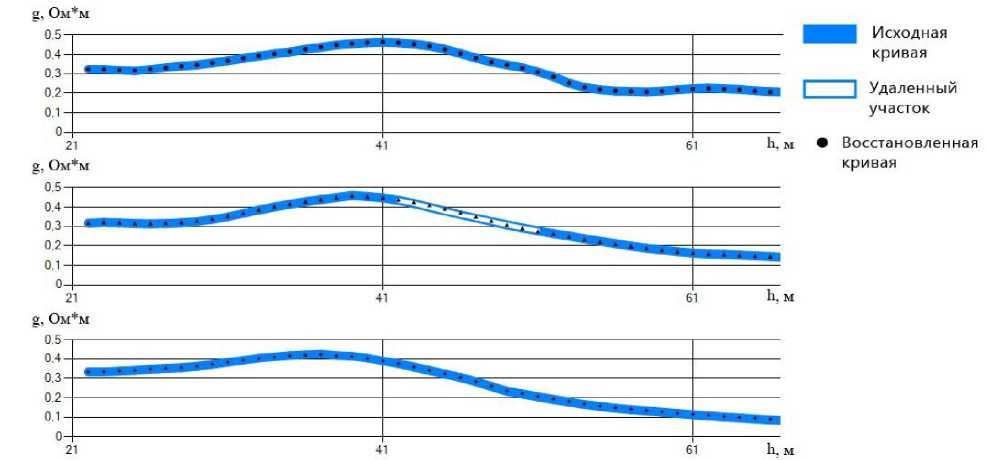
Рис. 3. Графическое представление содержимого LAS-файла с удалённым контролируемым участком

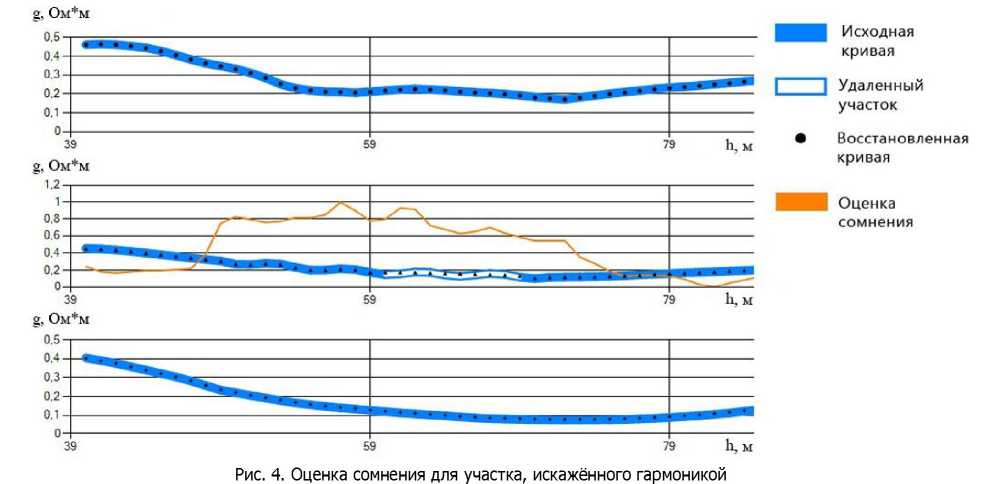
Точки — данные, восстановленные методом SOM.

Далее из исходных данных отброшенного участка вычитаем данные полученные методом восстановления, получая, таким образом, дискретно заданную случайную величину — кривую уклонений е. Величина среднеквадратического отклонения е и есть оценка достоверности для тестируемой точки, расположенной в центре отброшенного участка. Все операции повторяются для каждой точки, формируя кривую оценки достоверности.

Приведём результаты расчётов для рассматриваемой задачи контроля качества записи данных каротажа КС с использованием методов итерационного моделирования неполных данных самоорганизующимися многообразиями.

С целью проверки эффективности предложенного алгоритма на участке от 50 до 70 метров на испытуемой кривой были искусственно внесены помехи, представляющие собой гармонические колебания постоянной частоты и постоянной малой амплитуды. Участок с помехами явно выделялся аномально высоким уровнем среднеквадратического отклонения (рис. 4, 5).

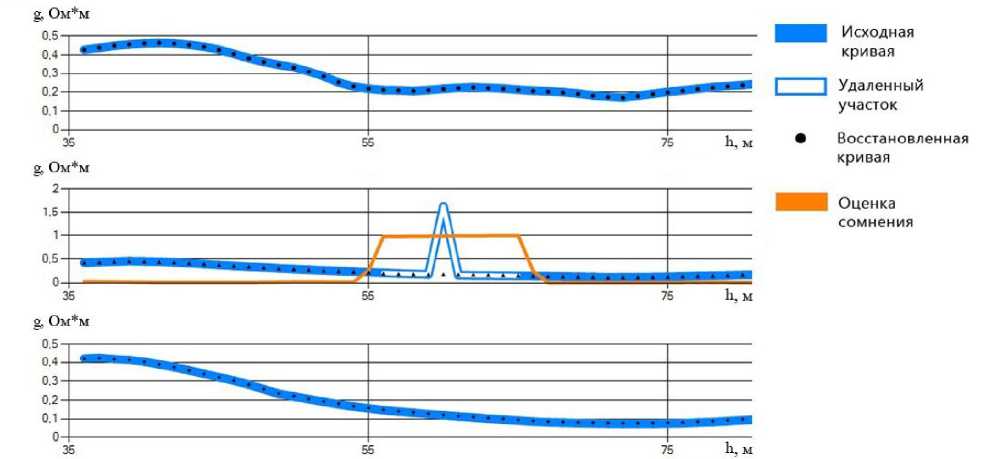
Рис. 5. Оценка сомнения для участка, искажённого выбросом

Заключение. Сформулирована задача автоматизированного контроля качества ГИС с использованием методов восстановления данных. Построена вычислительная схема, алгоритмы и программа вычислительной машины для решения задачи контроля качества ГИС. Доказана возможность применения методов восстановления данных в задачах оценки качества. Методика основана на использовании методов теории подобия и восстановления данных с пропусками. Автоматизация первичного контроля каротажных материалов позволит избежать дополнительных выездов на скважины с целью повторного проведения ГИС.