К вопросу идентификации проектных параметров наноспутника в процессе полёта

Существенный прогресс в области микроэлектроники и стремление обеспечить минимальную стоимость разработки и создания космического аппарата привели к появлению такого класса космических аппаратов, как наноспутники (НС). В настоящее время НС всё чаще применяются для реализации разнообразных космических миссий — обеспечения глобальной сети связи [1], инспекции космических объектов [2–4], дистанционного зондирования Земли [5–7] и т. д. Необходимость решения этих актуальных фундаментальных и прикладных задач предполагает развёртывание низкоорбитальных группировок НС [8–11], в которых каждый участник должен обладать повышенной манёвренностью, энергообеспеченностью и автономностью.

Невысокая энергетика и ограниченный объём пространства для размещения полезной нагрузки требуют использования на борту НС различных трансформируемых конструкций (раскрывающиеся солнечные панели, выдвижные штанги с аппаратурой и т. д.). Кроме того, на НС часто размещаются двигательные установки, которые в процессе решения целевых задач расходуют рабочее тело, что приводит к необходимости рассмотрения НС как тела переменного состава. В результате вышеперечисленных обстоятельств заметно изменяются инерционные и аэродинамические характеристики НС, а также запас статической устойчивости, что крайне важно для низкоорбитальных миссий, для которых влияние атмосферы Земли на характер движения является существенным. Так, в работе [12] исследовалось влияние трансформируемых конструкций НС на его аэродинамические характеристики, и было показано, что неучёт трансформируемых конструкций приводит к погрешности оценки аэродинамических характеристик НС 15–20%, что влияет на динамику его углового движения.

Вышеописанные особенности требуют рассмотрения НС как объекта с переменными тензором инерции, положением центра масс и центра давления. Изменения этих параметров оказывают влияние на функционирование системы управления НС. Работа [13] исследует влияние погрешности знания моментов инерции на погрешность реализации процедуры переориентации, например, погрешность знания моментов инерции 5–10% приводит к погрешности переориентации 8-10°.

Процедура идентификации может быть реализована двумя различными способами в зависимости от подхода к обработке измерительной информации. Первый способ — идентификация по накопленной выборке измерений предполагает формирование массива измерений на определённом интервале времени и его последующую обработку. Данный способ впервые был реализован В.В. Белецким в 1961 г. при обработке магнитометрических измерений с борта космического аппарата «Спутник-3» [14]. При использовании данного способа широкое распространение получила обработка измерений, основанная на методе наименьших квадратов. В работах [15–20] рассмотрены подходы к оценке различных характеристик космических аппаратов (параметры углового движения, инерционные характеристики). Для обработки измерений использовались методы Гаусса– Ньютона [18–20], Левенберга–Марквард-та [16, 17] и дифференциальной эволюции [15]. Погрешность процедуры оценки параметров космических аппаратов составила 5–15%.

Второй способ — идентификация в темпе поступления измерений, при котором оценки параметров непрерывно уточняются в процессе обработки информации. При этом наиболее популярными являются подходы, основанные на реализации расширенного фильтра Калмана [21, 22]. Такие подходы часто используют при осуществлении процедуры активной идентификации с использованием управляющих моментов [23, 24]. Погрешность оценки инерционных параметров космических аппаратов при таком подходе составляет 3–7%.

Однако, ввиду существенно ограни- ченных вычислительных ресурсов на борту НС, более приемлемой является реализация процедуры идентификации по накопленной выборке измерений.

Таким образом, реализация современных космических миссий с исполь- зованием НС решения на са обратных

вызывает необходимость борту НС комплек-задач параметрической идентификации, результаты решения которых могут быть использованы в контуре системы управления движением для повышения качества процесса управления, а также при оперативном анализе полётной информации для выявления признаков нештатного функционирования.

Особенно актуальной оценка текущих проектных параметров НС становится в условиях априорной неопределённости как внешних [25], так и внутренних факторов [22, 26–28], влияющих на процессы управления космическим аппаратом. Включение процедуры идентификации в контур системы управления движением позволит повысить качество процессов управления за счёт формирования дополнительной обратной связи по изменяющимся в процессе функционирования проектным параметрам космического аппарата.

В данной работе сформирована и исследована область применимости процедуры идентификации проектных параметров НС, изменяющихся в процессе полёта. При этом рассматривалась оценка таких проектных параметров, как безразмерные коэффициенты инерции и коэффициенты, учитывающие влияние аэродинамического момента на угловое движение.

постановка задачи

Угловое движение низкоорбитальных НС описывается системой динамических уравнений Эйлера [18, 19]:

ω^. _x = μ ( ω _y ω _z – ν _G a ₂₁ a ₃₁ ) + ε _{a x} ,

ω^. = ( ω ω – ν a a ) + ε , (1)

y Хц ^{11 317} 1 + Хц a y’ ^{V 7}

ωz = –(1 – λ + λμ)(ωxωy – νGa11a21) + λεaz и кинематических уравнений в кватернионах [15]:

q^. = ωq ,

Ix            Iy – Iz где λ = I и μ = I — безразмерные коэффициенты инерции; q — кватернион ориентации; ω = (ωx ωy ωz) — вектор угловой скорости; νG

3 µ _e r ³

— коэффициент

гравитационного момента.

В правых частях динамических уравнений также учитывается угловое ускорение, вызванное влиянием аэродинамического момента, ε = ( K a × v c )| v c | ρ , где v _c — вектор орбитальной скорости в связанной системе координат;

Ka = 2I CDSd — вектор конструктивных x коэффициентов аэродинамического момента; Ix — момент инерции вокруг оси X; CD — коэффициент аэродинамического сопротивления; S — характерная площадь НС; d — вектор, определяющий положение центра давления относительно центра масс НС; ρ — плотность атмосферы на высоте полёта НС. Так как в статье рассматривается угловое движение НС с типовыми проектно-баллистическими характеристиками без привязки к конкретной ориентации орбиты по отношению к Солнцу, то при расчётах использовалась модель плотности атмосферы для среднего уровня солнечной активности с усреднением на интервале сбора измерительной информации.

Состав вектора оцениваемых параметров математической модели углового движения НС представлен следующим выражением:

b = ( λ μ K _а ).

Широкое применение на НС получила система измерений, включающая в себя магнитометр и/или датчик угловой скорости (ДУС), созданные на базе МЭМС-технологий. Это объясняется тем, что такие измерительные средства имеют невысокую стоимость, приемлемую точность, малые габариты и энергопотребление.

Измерения ω(t), получаемые с ДУС, моделируются решением динамических уравнений Эйлера (1). Учитываются случайные погрешности измерений в виде аддитивного вектора случайной величины wω, компоненты которого независимы и распределены по нормальному закону с нулевым математическим ожиданием и заданным среднеквадратическим отклонением σω. Измерения магнитометра формируются с использованием модели IGRF [29], а случайные погрешности — аналогично погрешностям ДУС.

Инструментальные погрешности, отражающие смещение нуля, изменение линейной характеристики датчика, не учитываются в данной работе, однако могут быть также включены в расширенный вектор оцениваемых параметров. Таким образом, математические модели измерений для ДУС и магнитометра запишутся в следующем виде:

C _m ⁽ b , t ) = ^ю изм ( t ) = ^ ( b , t ) + wM, t );

CB(b, t) = Визм(t) = A(b, t)Ворб + wB(^B, t), где A(b, t) — матрица перехода из орбитальной в связанную систему координат [15]; Bорб — вектор напряжённости магнитного поля Земли в орбитальной системе координат, рассчитанный по модели IGRF.

Для построения области применимости процедуры идентификации в работе предлагается использовать модель проектно-баллистических параметров типового НС. Параметры данной модели получены из анализа статистики запусков НС [30].

В дальнейшем рассматриваются НС наиболее популярного формата CubeSat-3U [31] массой 3 кг. Исследования проведены для типового НС, который близок к динамически симметричному телу ( X « 1,01; ц ~ -0,85), при этом коэффициенты K _{а х} , K _а z ^ 0, а K _а y ~ 0,003 м/кг, что соответствует смещению центра масс НС только по продольной оси. Так как НС чаще всего запускаются с МКС [31], высота орбиты принимается равной 400 км. Модуль угловой скорости принимается равным |ш | ~ 1 ° /c, что соответствует транспортно-пусковым контейнерам (ТПК), изготавливаемым на предприятиях ГК «Роскосмос» [32], а при использовании коммерческих бюджетных ТПК, например, фирмы ISIS , может достигать значений до 65 ° /с [33].

Задача идентификации вектора b НС формулируется следующим образом: выполнить идентификацию вектора проектных параметров b по выборке векторов измерений, проводимых на борту НС в течение заданного интервала времени Т. Поставленная задача решается путём минимизации следующей целевой функции [15]:

N

J(b, T) = ^>1(C(t)) - C(b, t)))2 ^ min, где C(t) — вектор измерений; C(b, t) — модельное значение вектора измерений;

N = ^- — число измерений; A t — шаг измерений; T — интервал сбора измерительной информации.

Для оценки погрешности идентификации i -го компонента вектора b используется следующее выражение [34]:

" ^,„„ _ ^d J ( B , T ) .

δ b_i ⁼     ∂ b i ^;

δ b i

d J (b, 7 ) V¹

σ ²

_{∂ b}          изм

z

Формирование области погрешностей 8X , 5ц и 5 K _{а y} производилось на интервалах сбора измерительной информации 1 000…15 000 с. Измерения проводились с шагом A t = 10 c. Характеристики измерительных средств отражают точность бортовых измерительных средств НС, доступных на рынке. Так, в данной работе моделировались измерения магнитометров с погрешностями ст B 20^300 нТл и ДУС с погрешностями ст_ш 0,01^0,11 ° /c. Выбор величин ст B и ст_ш обоснован широким использованием на борту НС измерительных средств с характеристиками, находящимися в представленных диапазонах [30] .

∂ J ( b i , T )

Производные        решались численно

∂b г в окрестностях истинных значений искомых параметров. Для каждого расчётного случая проводилось 100 моделирований.

результаты моделирования

На рис. 1 представлены функции распределения погрешностей оценки компонент вектора b , построенные по результатам статистического моделирования ДУС c наилучшими и наихудшими точностными характеристиками и времени накопления измерений 1 000 и 15 000 с.

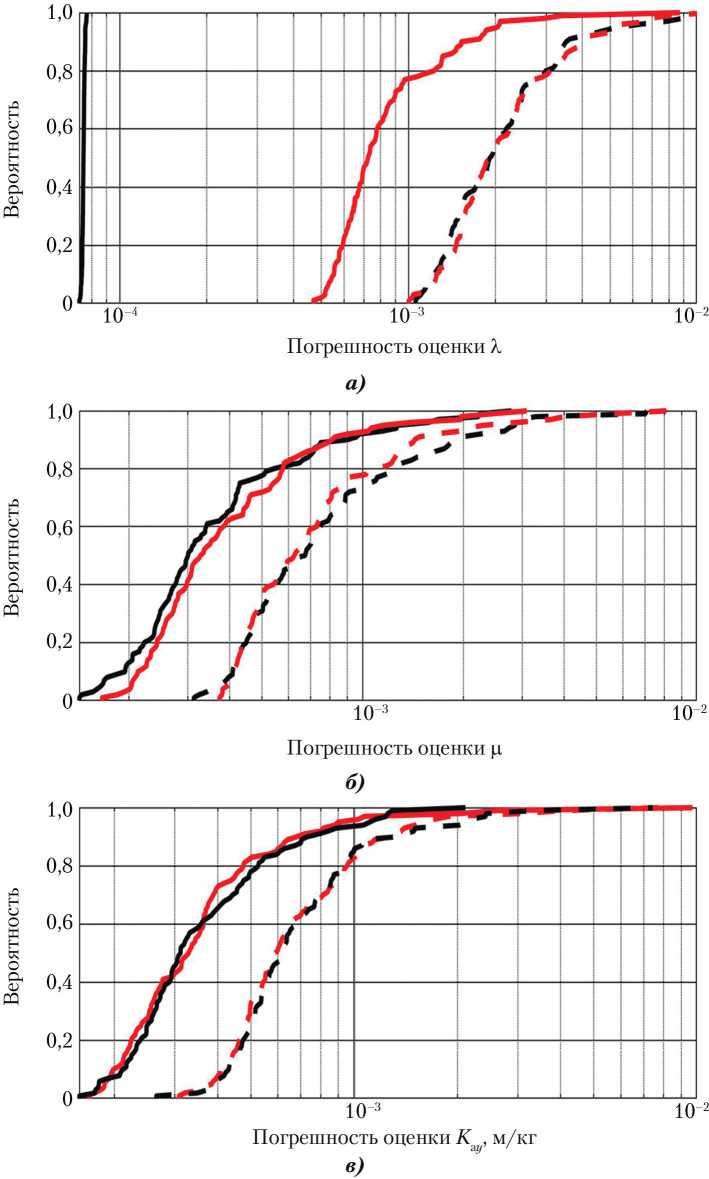
Рис. 1. Функции распределения погрешностей оценки компонент вектора b: a — параметра X ; б — параметра ц ; в — параметра К а ; ^{— — —} — а_т = 0,11 ° /с, T = 1 000 с; ^— - 0,11 ° /с, T = 15 000 с; “ — — — — ^ „ "= 0,01 ° /с, T = 1 000 с; ^— — а_т = 0,01 ° /с, T = 15 000 с

Примечание. Измерительное средство — датчик угловой скорости.

Результаты статистического моделирования показали эффективность использования ДУС при оценке параметра X , так как данный параметр характеризует динамическую симметрию НС, а значит и степень связанности каналов угловой скорости НС. Малые изменения X приводят к существенному изменению динамики вращения НС. Погрешность оценки параметра ц слабо зависит от характеристик ДУС, однако наблюдается ожидаемое снижение величины погрешности при увеличении времени накопления измерительной информации, что иллюстрирует рис. 2.

Показана неэффективность использования ДУС при оценке конструктивного аэродинамического коэффициента K _{а y} — погрешность оценки сопоставима с величиной оцениваемого параметра. Это связано с тем, что влияние аэродинамического момента не приводит к достаточному изменению угловой скорости НС на рассматриваемых промежутках времени. На более продолжительных интервалах времени неопределённость параметров модели атмосферы Земли затрудняет прогнозирование и расчёт углового движения НС, что делает нецелесообразным использование ДУС в этих целях.

На рис. 3 представлены функции распределения

Полученные функции (рис. 1–3) формируют границы области распределения погрешностей оцениваемых параметров. В табл. 1 приведены максимальные погрешности оценки компонент вектора b для доверительной вероятности P = 0,95.

погрешностей оценки компонент вектора b , построенные по результатам статистического моделирования при использовании магнитометра. Приведены функции распределения только для наиболее и наименее точных магнитометров и для времени накопления измерений 1 000 и 15 000 с.

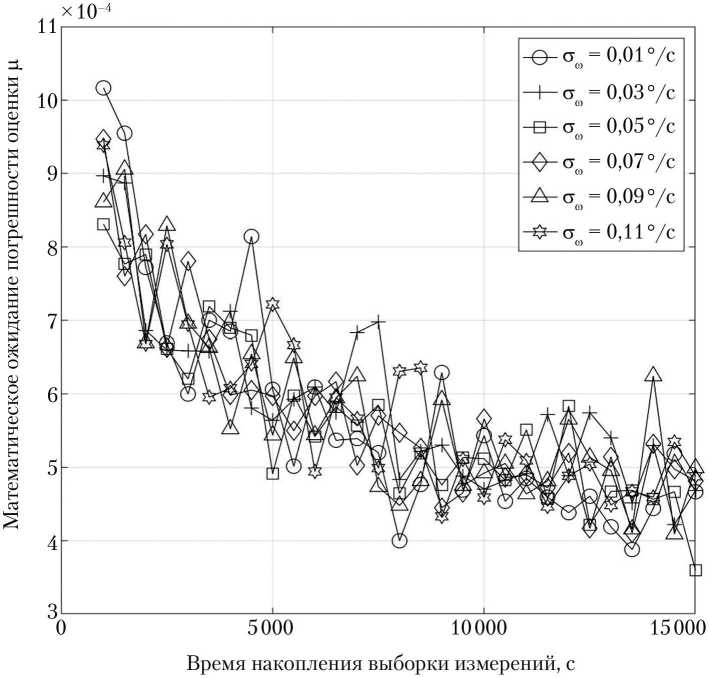
Рис. 2. Математическое ожидание погрешности оценки μ Примечание. Измерительное средство — датчик угловой скорости.

Представленные на рис. 5–7 зависимости формируют границы области распределения погрешностей оцениваемых параметров. В табл. 2 приведены максимальные погрешности оценок компонент вектора b для вероятности P = 0,95.

Выполненный анализ эффективности различных измерительных средств НС показал, что магнитометр является предпочтительным измерителем в задаче идентификации вектора b . При использовании высокоточного магнитометра для оценки параметра K _{а y} на продолжительном интервале сбора измерительной информации относительная погрешность оценки составила ~2%. В то же самое время погрешности оценки безразмерных коэффициентов инерции сопоставимы с погрешностями, полученными при использовании ДУС.

Было проведено дополнительное статисти- ческое исследование оценки эффективности использования ДУС для компонент вектора b

идентификации

при движении НС с высокой угловой скоростью |w| ~ 10 °/c. Такая величина угловой скорости может возник- нуть при использовании коммерческих

ТПК для отделения НС от носителя.

Таблица 1

максимальные погрешности оценок компонент вектора b для вероятности P = 0,95

Параметр	Истинное значение	T = 1 000 с		T = 15 000 с
		ст „ = 0,01 ° /c	ст „ = 0,11 ° /c	ст „ = 0,01 ° /c	ст „ = 0,11 ° /c
X	1,01	0,0053	0,0053	0,00008	0,002
Ц	–0,85	0,003	0,002	0,0013	0,0011
K а y , м/кг	0,003	0,0021	0,0015	0,0011	0,0009

Таблица 2

максимальные погрешности оценок компонент вектора b для вероятности P = 0,95

Параметр	Истинное значение	T = 1 000 с		T = 15 000 с
		ст B = 20 нТл	ст B = 300 нТл	ст B = 20 нТл	ст B = 300 нТл
X	1,01	1∙10–5	2∙10–3	2,2∙10–6	3,4∙10–5
Ц	–0,85	2∙10–3	1,6∙10–3	3∙10–5	1∙10–3
K а y , м/кг	0,003	1,8∙10–3	1,9∙10–3	6∙10–5	1∙10–3

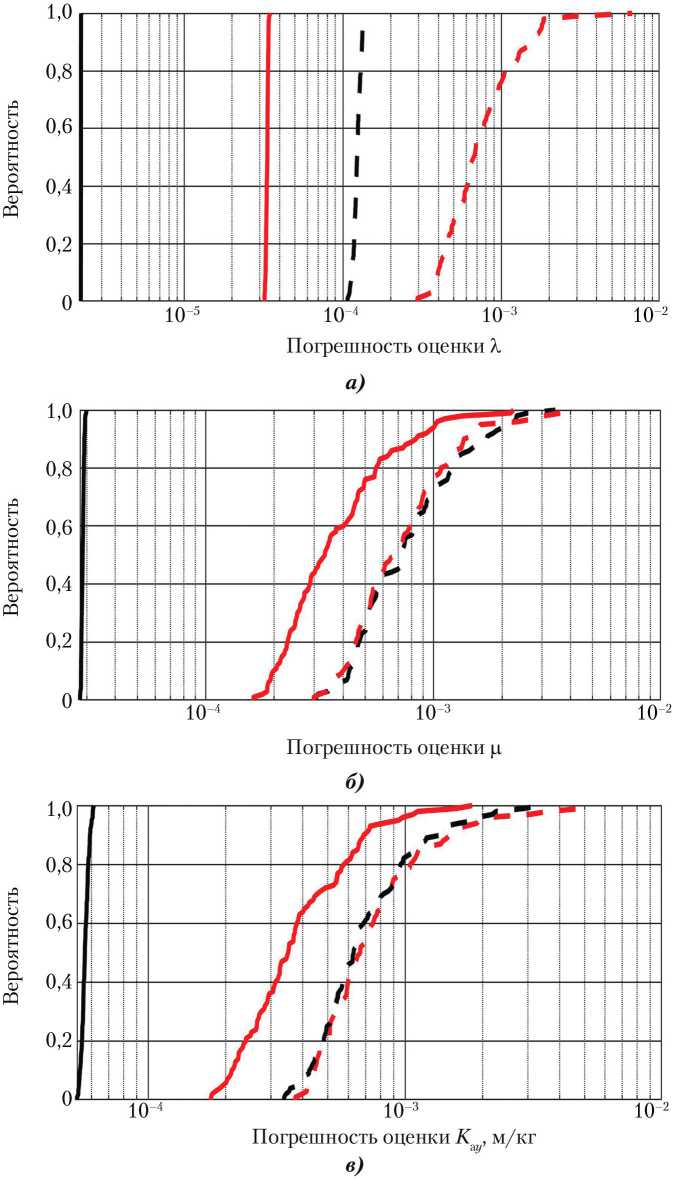
3. Функции распределения погрешностей оценки компонент вектора b:

Рис.

σ _B = 300 нТл,

—

20 нТл, T = 1 000 c;

a — параметра X ; б — параметра ц ; в — параметра K y ; ■ ■ ■

T = 1 000 с; ^^^" — ст B = 300 нТл, T = 15 000 с; ■ ■ ■ — ст B ^^^" — ст B = 20 нТл, T = 15 000 с

Примечание. Измерительное средство — магнитометр.

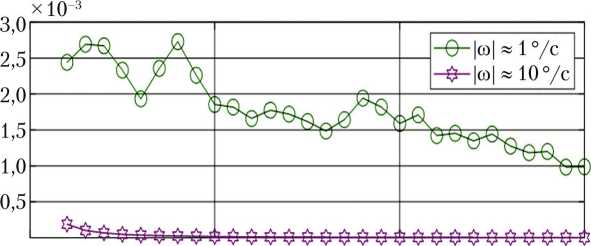
На рис. 4 приведены погрешности оценки параметров λ , μ при различной угловой скорости движения НС. Анализ результатов позволяет сделать вывод, что погрешность оценки параметров уменьшается при увеличении угловой скорости НС.

модели распределения погрешностей идентифицируемых параметров

Аналитические модели распределения погрешностей идентификации вектора проектных параметров типового НС могут применяться для решения следующих задач:

• •    формирование циклограммы функционирования НС при мониторинге его проектных параметров в процессе полёта;

• •    оценка эффективности бортовых измерительных средств НС;

• •    формирование требований к бортовым измерительным средствам НС.

Модели могут применяться как на этапе проектирования космической миссии, так и при её реализации.

На основе проведённого обширного статистического моделирования построены функции распределения погрешностей идентификации δλ, δμ и δKаy. Проверка гипотез о законах распределения выполнялась по методу максимального правдоподобия [35]. Анализ сформированных выборок реализаций на соответствие нормальному, логнормальному и логистическому законам распределения показал, что распределение погрешностей лучше всего описывается логнормальным законом рас- пределения. Например, на рис. 5 приведены функции правдоподобия для нормаль ного, логнормального и ло

-

-

гистического распределений для параметра δλ при использовании магнитометра σ _B = 20 нТл. Значения функции правдоподобия для логнормального распределения оказались больше, чем для других законов. На малых интервалах времени разница составляет ~15%, а на длительных интервалах 5%.

s i

я и о

о

s

s я

о

s о с о я

Логнормальное распределение случайной величины x описывается двумя парамет-

рами

x

и ст x . Плотность

вероятности случайной величины x для такого закона описывается выражением

1 (ln x – θ _x )² f_X ( x ) =       ¹ e ^{2      σ x 2}     . (2)

x

Время накопления выборки измерений, с а)

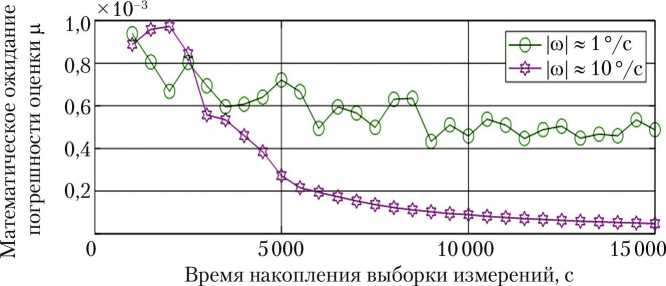
Рис. 4. Математическое ожидание погрешности оценок параметров: а — X ; б — ц

Примечание. Измерительное средство — датчик угловой скорости а_ш = 0,11 °/с.

Математическое ожидание случайной величины определяется как

σ² θ x + ^x M ( x ) = e   ²

.

Дисперсия случайной ве личины определяется выра жением

D ( x ) = ( e ^ст x - 1) e ^{2 9} x ^{+ ст} x ² .

Например, на рис. 6

ведены метров

зависимости распределения

-

-

при пара

-

-

9 дЛ

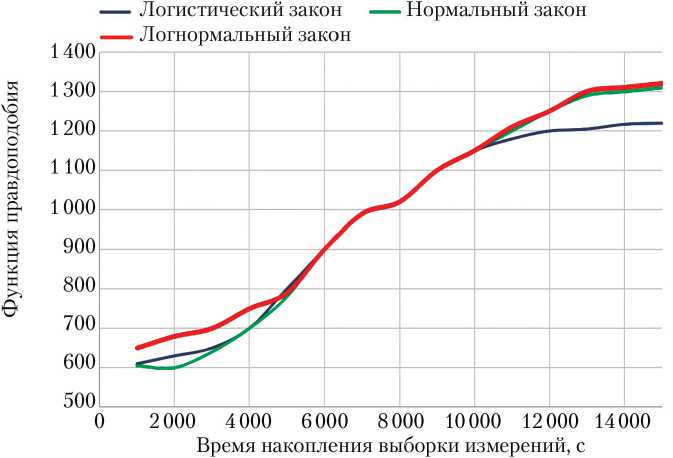
Рис. 5. Сравнение функций правдоподобия для различных законов распределения для параметра 8X

и ст _дЛ от времени накопления выборки измерений T и точности магнитометра ст _B .

Были получены аналитические функции параметров логнормального распределения погрешностей оценки вектора проектных параметров в зависимости от T и ст _изм путём аппроксимации результатов численных экспериментов функцией вида

^{Ф ( ст} изм , T ) = Р 00 ⁺ Р 10 ^СТ изм ⁺

⁺ Р 01 ^{T +} Р 20 ^ст изм ⁺ Р 11 ^ст изм ^{T +}

23   2

^Р 02         ^Р 30 ^ст изм ^Р 21 ^ст изм

+ Р ₁₂ ст _изм

T ² + p 03 T ³ .

Следует отметить, что поведение функций правдоподобия, приведённых на рис. 5, характерно и при использовании ДУС. Логнормальный закон более адекватен результатам проведённого параметрического анализа и может быть принят для описания распределения погрешностей идентификации на всех промежутках времени.

Исследование показало, что выбор третьей степени аппроксимирующей функции является достаточным в рассматриваемой задаче. Использование аппроксимаций более высокого порядка не сказывается на последующих результатах.

Значения коэффициентов аппроксимирующей функции при использовании магнитометра приведены в табл. 3.

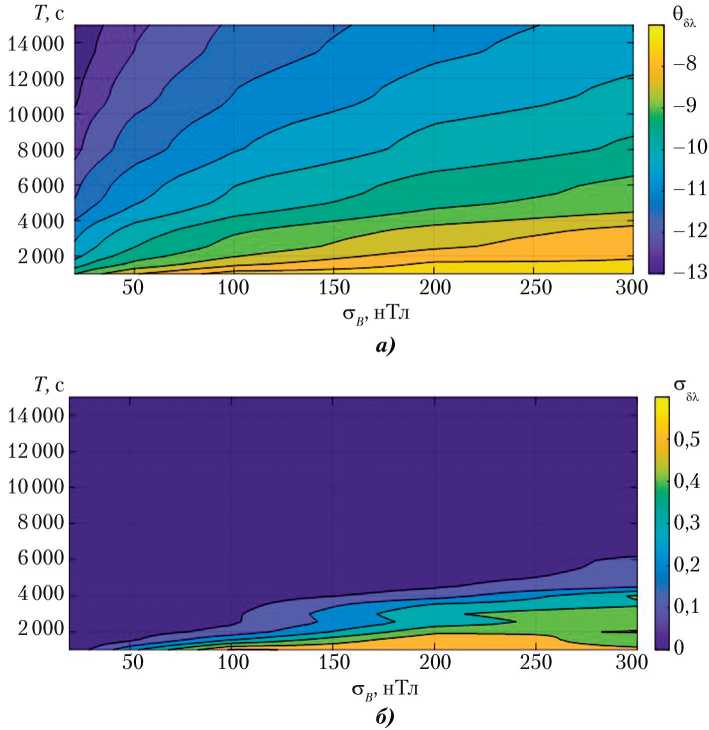
Рис. 6. Зависимости параметров законов распределения от времени ния выборки измерений T и погрешности магнитометра σB: б — параметра σδλ накопле- a — параметра θδλ;

Аналогичным образом были получены аналитические зависимости параметров распределения σδμ, σδλ, σδKay, θδμ, θδλ и θδKay в случае использования ДУС. Значения коэффициентов аппроксимирующей функции при использовании ДУС приведены в табл. 4.

Таким образом, аппроксимирующие функции с коэффициентами из табл. 3, 4, а также соотношения (2)–(4) позволяют получить аналитические выражения для плотности вероятности, математического ожидания и дисперсии погрешностей идентификации параметров НС, которые могут быть использованы разработчиками НС как на этапе проектирования, так и при эксплуатации на орбите.

иллюстрация применения полученных моделей

Иллюстрация использования разработанных моделей приведена на примере двух задач для типового НС, запускаемого с МКС: первая должна решаться при выборе циклограммы работы бортовых систем НС на этапе формирования полётного задания, вторая — при выборе состава измерительных средств на этапе создания НС, обеспечивающих решение целевой задачи.

Таблица 3

значения коэффициентов p аппроксимирующей функции при использовании магнитометра

p	θ δμ ( σ B , T )	θ δλ ( σ B , T )	θδ K a y ( σ B , T )	σδμ ( σ B , T )	σδλ ( σ B , T )	σ δ K a y ( σ B , T )
p 00	–7,631	–9,426	–7,316	0,442	0,022	0,526
р 10	0,011	0,0211	0,0128	0,003	0,0006	0,002
p 01	–2,156∙10–4	–4,829∙10–4	–2,338∙10–4	–4,562∙10–5	0	–3,003∙10–5
p 20	–3,719∙10–5	–3,903∙10–5	–1,217∙10–4	–9,457∙10–6	0	–7,778∙10–6
p 11	–6,752∙10–7	–1,755∙10–8	1,745∙10–6	1,668∙10–7	–8,245∙10–8	1,444∙10–7
p 02	0	1,58∙10–8	1,862∙10–9	0	9,785∙10–10	–5,378∙10–10
p 30	0	0	2,702∙10–7	0	0	0
p 21	0	0	4,212∙10–9	0	0	0
p 12	0	0	3,07∙10–12	0	0	0
p 03	0	0	0	0	–3,319∙10–14	0

Таблица 4

значения коэффициентов p аппроксимирующей функции при использовании дуС

p	θ δμ ( σ ω , T )	θ δλ ( σ ω , T )	θ δ K a y ( σ ω , T )	σδμ ( σω , T )	σδλ ( σω , T )	σ δ K a y ( σ ω , T )
p 00	–7,213	–5,898	–7,196	0,6564	0,5115	0,5416
P 10	–0,087	10,43	–0,295	–2,619	6,91	–0,08
p 01	–9,042∙10–5	–0,0004	–9,413∙10–5	–1,034∙10–5	–0,0001	1,42∙10–6
p 20	0	–130,4	0	12,35	–87,27	0
p 11	3,988∙10–5	0,006	2,637∙10–5	0,0002	0,001	0
p 02	2,975∙10–9	1,867∙10–8	3,31∙10–9	–4,467∙10–10	5,906∙10–9	0
p 30	0	0	0	17,2	138,6	0
p 21	0	–0,014	0	–0,001	0,003	0
p 12	0	–1,406∙10–7	0	–4,085∙10–9	–6,316∙10–8	0
p 03	0	–3,432∙10–13	0	5,065∙10–14	–1,013∙10–13	0

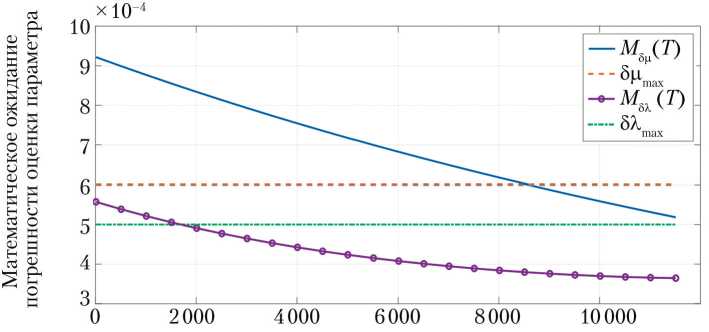
Задача 1. Для НС изменяемой конфигурации, оснащённого аэродинамическим стабилизатором [36], выбрать циклограмму работы бортовых измерительных средств (сформировать время накопления магнитометрических измерений для оценки инерционных характеристик — коэффициентов инерции НС с погрешностью δλ _max ≤ 0,0005 и δμ _max ≤ 0,0006), если бортовой магнитометр НС имеет точность σ _B = 250 нТл. Требования к погрешности оценки инерционных параметров формируются, исходя из возможности оценки перемещения аэродинамического стабилизатора. С использованием аппроксимирующей функции с коэффициентами из табл. 4 были получены зависимости, представленные на рис. 7.

Согласно рис. 7, требуемая точность оценки параметра λ достигается на интервале 1 700 с, а параметра μ — на интервале 8 700 с. Таким образом, для уточнения инерционных параметров НС с допустимыми погрешностями требуется накопление измерений на интервале ~9 000 с. Этот интервал времени должен быть учтён при формировании циклограммы полёта НС.

Задача 2. Сформировать требования к необходимой точности бортового магнитометра σ _B . Магнитометрические измерения используются для оценки коэффициентов инерции НС. Погрешность измерений должна позволять оценивать коэффициенты инерции НС с погрешностями не хуже 0,005 по параметру λ и не хуже 0,004 — по параметру μ . При выполнении миссии инерционные параметры (коэффициенты инерции НС) могут изменяться в пределах ± 5% от номинальных значений. Такое изменение коэффициентов инерции может наблюдаться при выработке рабочего тела за счёт работы двигательной установки НС [37].

Время накопления выборки измерений, с

Рис. 7. Зависимость математического ожидания погрешности оценки параметров λ и μ от времени накопления выборки измерений Т: σλ _max и σμ _max — допустимые погрешности оценки параметров λ и μ , соответственно

Допустимые погрешности оценки параметров выбраны на порядок меньше, чем изменения самих параметров. С использованием аппроксимирующей функции с коэффициентами из табл. 3 были получены графические зависимости, изображённые на рис. 8.

Согласно рис. 8, при заданных условиях задачи целесообразно использовать магнитометр с погрешностью измерений не хуже σ _B = 400 нТл, что соответствует показателям точности магнитометров, присутствующих на рынке измерительных средств и широко используемых в составе НС. Точностные характеристики магнитометра слабо влияют на оценку параметра μ .

заключение

Построены и исследованы области применимости различных измерительных средств в задаче идентификации параметров НС при его функционировании на орбите. Результаты параметрических исследований позволяют сделать вывод о предпочтительности использования ДУС для оценки инерционных характеристик НС ( λ , μ ). В этом случае возможно упрощение математической модели (1) за счёт неучёта воздействия аэродинамических сил. Такое решение может быть эффективным для НС переменной массы (например, оснащённого двигательной установкой), у которого инерционные характеристики более чувствительны к изменению массы, чем параметр K _{а y} .

Использование ДУС эффективно на коротких интервалах сбора измерительной

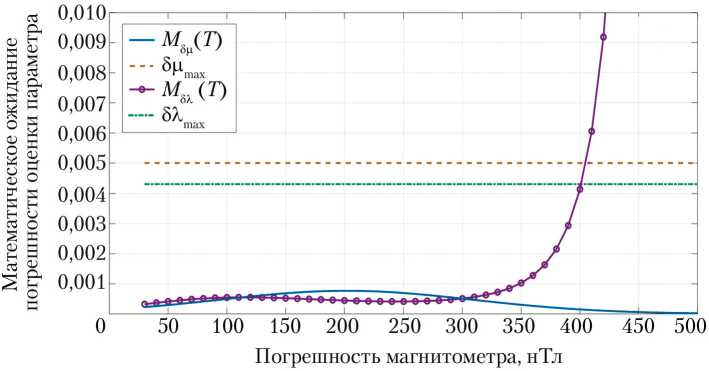
Рис. 8. Зависимость математического ожидания погрешности оценки параметров λ и μ от погрешности магнитометрических измерений σ _B: δλ _max и δμ _max — допустимые погрешности оценки параметров λ и μ , соответственно

информации, а также при движении НС с высокой угловой скоростью, например, на этапе отделения от носителя. При этом возможно использование математической модели (1) без учёта возмущающих моментов.

Для оценки аэродинамических характеристик НС ( K _{а y} ) требуется наличие на борту высокоточного магнитометра σ _B = 10…30 нТл. Интервал сбора измерительной информации должен составлять порядка трёх орбитальных витков. Для получения корректных результатов требуется привлечение модели (1), учитывающей влияние гравитационного и аэродинамического моментов.

Показано, что при оценке коэффициентов инерции НС абсолютная погрешность измерений ДУС не имеет определяющего значения. Основную роль играет относительная погрешность ДУС, определяемая через отношение σ_ω к модулю угловой скорости.

Выбран наиболее адекватный закон распределения погрешностей идентификации параметров НС (логнормальный закон распределения). Получены аналитические зависимости параметров закона распределения в зависимости от типа и характеристик измерительных средств и времени накопления выборки измерений для типового НС формата 3 U , которые могут быть использованы как на предварительном этапе проектирования НС, так и на этапе оперативного формирования полётного задания для уже созданного НС.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований (грант

РФФИ № 20-08-00617-А).