К вопросу комплексной оценки потенциала развития территорий и формирования зон совместного природопользования

• •    природно-ресурсное (A) – сохранение уникальных природных участков, научноисследовательское направление, возможности экологического туризма, просвещения;

• •    технико-экономическое (B) – промышленное освоение территории, размещение производств, добыча ресурсов;

• •    инфраструктурно-социальное (C) – размещение объектов социального, культурного, рекреационного назначения.

Современные методы проектирования, строительства, эксплуатации объектов позволяют в значительной мере снизить негативное влияние на окружающую среду, а в ряде случаев и улучшить экологическую ситуацию (например, снижение уровня браконьерства морских биоресурсов при промышленном освоении побережья). Наличие промышленного объекта создает визуальную доминанту и снижает рекреационную привлекательность территории, но при этом повышается уровень инфраструктурной обеспеченности, социальноэкономического благополучия привлекаемого населения. В тоже время стихийное размещение рекреационных объектов на побережье является серьезной нагрузкой на морские и прибрежные экосистемы [4]. Поэтому задача комплексной взвешенной оценке потенциала территории является интересной задачей, практическое применение которой возможно в области планирования развития территорий и экологической экспертизы [2].

Условно потенциал территории можно численно оценить в удельных единицах (уникальность ресурса), по общему числу населения, вовлекаемого в развитие территории, в финансовом выражении (прибыль от реализации проектов). Каждое из направлений можно представить в виде множества элементов, представляющих собой факторы, характеризующие основные показатели направления (потенциала). Можно задавать граничные условия для параметров, рассматривая отдельно положительные и отрицательные результаты взаимодействий. Таким образом, зона общих интересов будет представлена в двух аспектах, негативное влияние множеств друг на друга и позитивное влияние. Для математического описания метода введем следующие обозначения: А = {ai, i=1,…n} – множество А, содержащее набор элементов аi.

B = {b j , j=1,…m} – множество B, содержащее набор элементов b j .

C = {c k , k=1,…l} – множество C, содержащее набор элементов c k .

Для того, чтобы найти элементы общей области взаимодействия трех множеств А, В, С, рассмотрим влияние элементов каждого множества на элементы других множеств. Результатом такого влияния будут новые множества, представленные в виде:

F h = {a i b j , a i c k , b j c k , i=1,…n, j=1,…m, k=1,…l}, h=1,2,3

При большом количестве элементов во множествах, будет целесообразным построить таблицы взаимовлияния следующего вида:

Таблица 1. Таблица взаимовлияния элементов множеств А и В

A B	a 1	a 2		a n
b 1	a 1 b 1	a 2 b 1		a n b 1
b 2	a 1 b 2	a 2 b 2		a n b 2
b m	a 1 b m	a 2 b m		a n b m

Таблица 2. Таблица взаимовлияния элементов множеств В и С

C B	c 1	c 2		c l
b 1	c 1 b 1	c 2 b 1		c l b 1
b 2	c 1 b 2	c 2 b 2		c l b 2
b m	c 1 b m	c 2 b m		c l b m

Таблица 3. Таблица взаимовлияния элементов множеств С и А

C A	c 1	c 2		c l
a 1	c 1 a 1	c 2 a 1		c l a 1
a 2	c 1 a 2	c 2 a 2		c l a 2
a n	c 1 a n	c 2 a n		c l a n

При небольшом количестве элементов можно использовать схему попарного взаимодействия. Пример использования схемы попарного взаимодействия приведен в данной статье при рассмотрении частного случая нахождения общей зоны взаимодействия трех шестиэлементных множеств. Таким образом, получим три новых множества F 1 , F 2 , F 3 и перейдем к нахождению общей области взаимодействия.

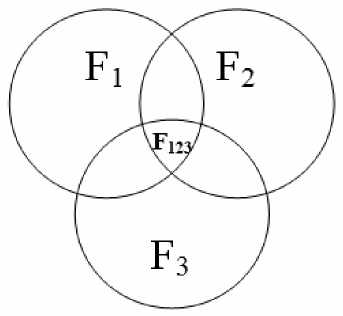
Рис. 1. Схема взаимодействия множеств F 1 , F 2 , F 3

Нахождение общей области взаимодействия трех множеств проведем в два этапа:

• 1.    Результатом взаимодействия двух множеств будет их пересечение (результирующее множество), но не все факторы каждого множества участвуют в данном взаимодействии. Для нашего случая будет три неодинаковых варианта пересечений множеств (а именно, n !

C = —7----r- - число сочетаний без повторе-

• m! ( n - m )!

ний, где n – количество элементов, m – количество элементов в одном сочетании)

• a)    F i I F , = F

F 12 = F 1 ∩F 2 = {a i b j | a i b j    F 1     a i b i    F 2 }

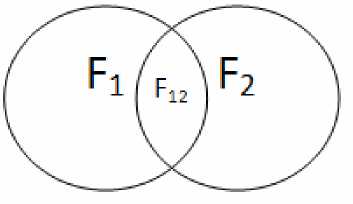
Рис. 2. Схема взаимодействия множеств F 1 и F 2

• b)    F ₂1 F 3 = F 23

F 23 = F 2 ∩F 3 = {b j c k | b j c k    F 2     b i c k    F 3 }

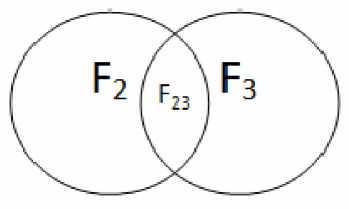
Рис. 3. Схема взаимодействия множеств F 2 и F 3

• c)    F 3 I F = F

• 2.    К результату попарного взаимодействия добавим третье множество. Учитывая свойство ассоциативности пересечений множеств, результат не будет зависеть от того, с какого множества был начат расчет.

F 31 = F 3 ∩F 1 = {c k a i | c k a i F 3     c k a i F 1 }

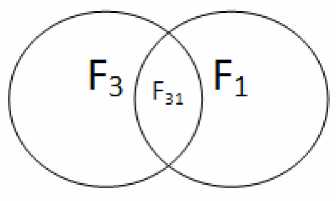
Рис. 4. Схема взаимодействия множеств F 3 и F 1

F 231 =F 23 ∩F 1 ={ a i b j c k | a i b j , b j c k F 23 a i c k F 1 } ^{c) F} 31 ¹ F 2 = F 312 ⁼ F 231 ⁼ F 123

F 312 =F 31 ∩F 2 ={ a i b j c k | b j a i , a i c k F 31 b j c k F 2 }

Таким образом, мы получили множество F ₁₂₃ = F ₂₃₁ = F ₃₁₂ с элементами a i b j c k , являющееся результатом взаимодействия трех множеств F 1 , F 2 , F 3 . Заметим, что в практическом приложении нет необходимости рассматривать попарное взаимодействие каждых двух множеств с последующим добавлением третьего множества, для получения результата взаимодействия трех множеств достаточно будет рассмотреть пересечение любых двух множеств с последующим добавлением оставшегося. Для более полного понимания математического аппарата взаимодействия, рассмотрим частный случай для трех шестиэлементных множеств. Введем следующие обозначения:

Множество A, A = {a 1 a 2 a 3 a 4 a 5 a 6 } Множество B, B = {b 1 b 2 b 3 b 4 b 5 b 6 } Множество C, C = {c 1 c 2 c 3 c 4 c 5 c 6 }

Обратим внимание, что количество элементов множеств может быть различным. В данном примере рассмотрен вариант с одинаковым количеством элементов для наглядной демонстрации взаимодействия. Введем произвольную схему попарного взаимодействия множеств:

a) F 1 F 2 = F 123

F 123 =F 12 ∩F 1 ={ a i b j c k | c k b j , a i b j F 12     c k a i F 3 }

b) F 23 I F = F 231 = F 23

ai	a2	1          a3	34           |	a5	at
					1 r
bl	b2	1         b3	b4         1		b6_
C1	C2	1            =3
				V
	a2	1          33		a?

Рис. 5. Схема попарного взаимодействия

Для удобства результаты занесем в таблицы:

Таблица 4. Взаимодействие с множеством A

a 1 b 1 a 1 b 2 a 1 c 1

a 2 b 2 a 2 c 2 a 2 c 4

a 3 b 2 a 3 b 5 a 3 c 1 a 3 c 3

a 4 b 4 a 4 c 4 a 4 c 6

a 5 b 5 a 5 c 5

a 6 b 4 a 6 b 6 a 6 c 5 a 6 c 6

Таблица 5. Взаимодействие с множеством B

b 1 a 1 b 1 c 1 b 1 c 2

b 2 a 1 b 2 a 2 b 2 a 3 b 2 c 3

b 3 c 3 b 3 c 4

b 4 a 4 b 4 a 6

b 5 a 3 b 5 a 5 b 5 c 6

b 6 a 6 b 6 c 4

Таблица 6. Взаимодействие с множеством C

c 1 b 1 c 1 a 1 c 1 a 3

c 2 b 1 c 2 a 2

c 3 b 3 c 3 b 2 c 3 a 3

c 4 b 3 c 4 b 6 c 4 a 2 c 4 a 4

c 5 a 5 c 5 a 6

c 6 b 5 c 6 a 4 c 6 a 6

На основании полученных данных сформируем новые множества, состоящие из результатов попарного взаимодействия для каждого множества:

F 1 = {a 1 b 1 a 1 b 2 a 1 c 1 a 2 b 2 a 2 c 2 a 2 c 4 a 3 b 2 a 3 b 5 a 3 c 1 a 3 c 3 a 4 b 4 a 4 c 4 a 4 c 6 a 5 b 5 a 5 c 5 a 6 b 4 a 6 b 6 a 6 c 5 a 6 c 6 }

F 2 = {b 1 a 1 b 1 c 1 b 1 c 2 b 2 a 1 b 2 a 2 b 2 a 3 b 2 c 3 b 3 c 3 b 3 c 4 b 4 a 4 b 4 a 6 b 5 a 3 b 5 a 5 b 5 c 6 b 6 a 6 b 6 c 4 }

F 3 = {c 1 b 1 c 1 a 1 c 1 a 3 c 2 b 1 c 2 a 2 c 3 b 3 c 3 b 2 c 3 a 3 c 4 b 3 c 4 b 6 c 4 a 2 c 4 a 4 c 5 a 5 c 5 a 6 c 6 b 5 c 6 a 4 c 6 a 6 }

Новые множества составляются путем объединения полученных данных по принципу наличия в паре элемента одного множества. Пары в новых множествах повторяются, так как они являются результатом взаимодействия. Выделение общей области взаимодействия трех представленных множеств, как описано выше, произведем в два этапа.

Первый этап – попарное взаимодействие:

F₁₂ = F₁∩F₂ = {a₁b₁ a₁b₂ a₂b₂ a₃b₂ a₃b₅ a₄b₄ a₅b₅ a 6 b 4 a 6 b 6 }

F 23 = F 2 ∩F 3 = {b 1 c 1 b 1 c 2 b 2 c 3 b 3 c 3 b 3 c 4 b 5 c 6 b 6 c 4 } F₃₁ = F₃∩F₁ = {c₁a₁ c1a₃ c₂a₂ c₃a₃ c₄a₂ c₄a₄ c₅a₅ c 5 a 6 c 6 a 4 c 6 a 6 }

Второй этап – присоединение третьего множе ства:

F 123 = F 12 ∩F 1 = {a 1 b 1 c 1 a 3 b 2 c 3 }

F 231 ≡ F 123 = F 23 ∩F 3 = {a 1 b 1 c 1 a 3 b 2 c 3 }

F 312 ≡ F 231 ≡ F 123 = F 31 ∩F 2 = {a 1 b 1 c 1 a 3 b 2 c 3 }

TO THE QUESTION OF COMPLEX POTENTIAL ESTIMATION THE

Как видно из полученных данных, конечный результат не зависит от порядка взаимодействия множеств, поэтому для получения результирующего множества достаточно использовать только одно объединение на каждом этапе.

Выводы: исходя из учета всех параметров начальных множеств (A, B, C), мы через промежуточные множества (F 1 , F 2 , F 3 , F 12, F 23, F 31 ) получили в общем виде результат взаимодействия трех множеств (F 123 ). Результат позволяет определить элементы, одновременно влияющие на все рассматриваемые множества. На практике предлагаемый метод может быть реализован в виде программного комплекса, алгоритма, позволяющего оценить тенденции развития территории (изменение потенциала), выявить наиболее проблемные факторы и показатели, разработать мероприятия по комплексному развитию территории.