К вопросу метрологической оценки метода акустической эмиссии как инструмента контроля процесса импрегнирования пористых материалов

Введение. Осуществление производственной деятельности человека в условиях жидких агрессивных сред в процессе эксплуатации связано с модифицированием свойств тканей защитной одежды. Модифицирование свойств текстильных материалов достигается, в первую очередь, их импрегнированием определённой жидкостью. Импрегнирование как процесс изменения свойств пористых тел при заполнении их пустот импрегнатом различного вида находит в настоящее время всё более широкое применение, а текстильные материалы, в свою очередь, представляют собой классический пример пористых тел [1].

Основная часть. Для полного представления о кинетике импрегнирования текстильных материалов необходимо изучить их капиллярные свойства, что позволит получить данные о процессах загрязнения их в результате контакта с агрессивными жидкостями, в том числе с нефтью, которая сопровождает профессиональную деятельность по нефтедобыче. Текстильные материалы способны поглощать жидкость при соприкосновении, под воздействием сил поверхностного натяжения и сорбции, что относится к разряду капиллярных явлений. К капиллярным явлениям, как правило, относят явления в жидкостях, которые вызваны искривлением их поверхности, граничащей с другой жидкостью, газом, собственным паром или твёрдым телом.

Возможность фиксирования таких сложных для улавливания деформаций, которые происходят не только на первой стадии проникновения жидкости по одному из каналов на обратную сторону текстильного материала, но и до момента полного насыщения текстильной структуры (простой и многослойной), в настоящей работе установлена при использовании акустикоэмиссионного метода [2, 8].

Метод акустической эмиссии (АЭ) при пропитке основан на фиксации акустических колебаний, возникающих в жидкости в результате образования, движения и последующего схлопывания газовых пузырьков. Газовые пузырьки образуются в результате заполнения пор и пустот в материале импрегнатом. Методика регистрации сигналов АЭ в жидкой среде описана в ряде публикаций [2—10], поэтому целью настоящей работы являлся, в первую очередь, анализ полученных экспериментальных данных.

Достоверно установлено, что с момента погружения образца пористого текстильного материала в жидкость регистрируется индуцирование акустических сигналов, причём их характеристики, в частности амплитуда, энергия и длительность, с самого начала свидетельствуют об индивидуальности процесса в зависимости от вида выбранной ткани.

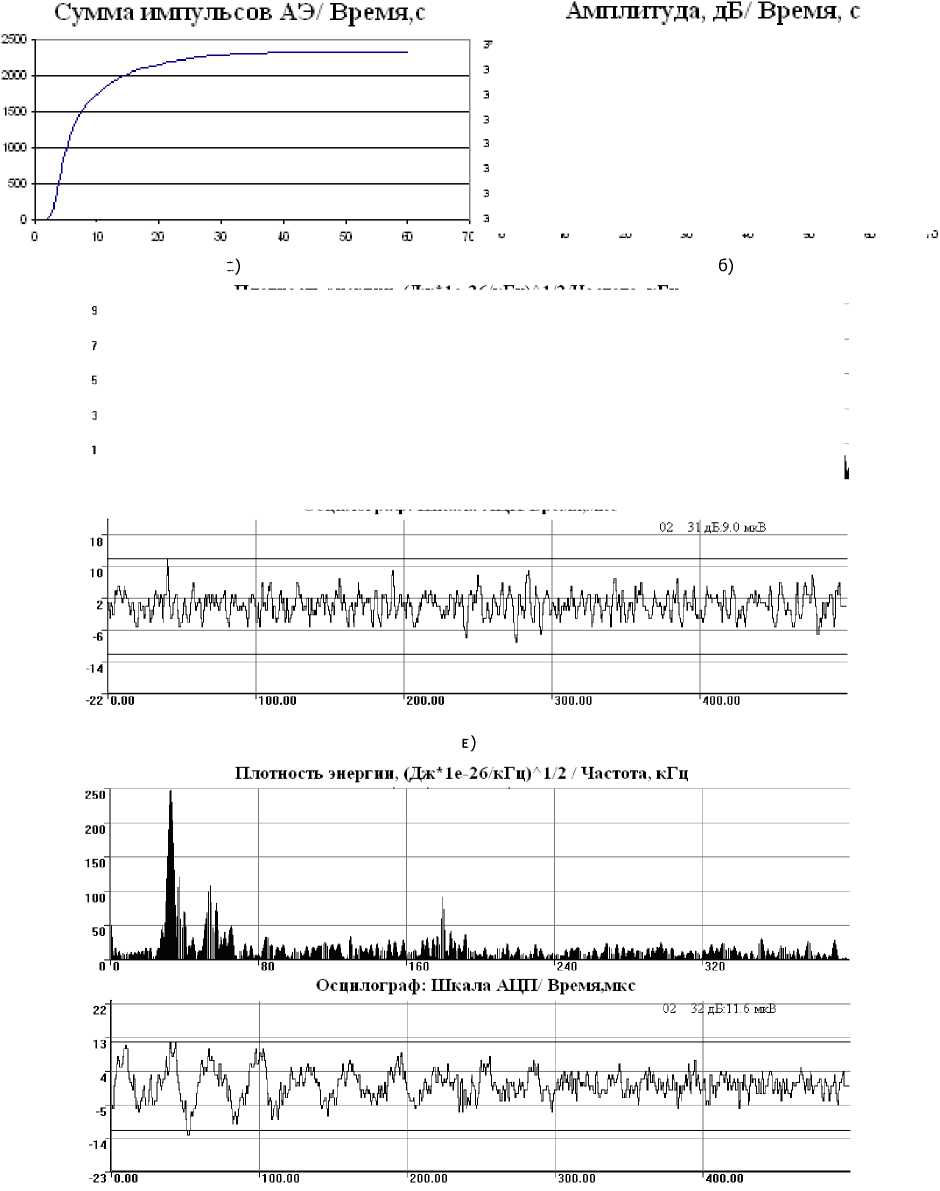
в)

г)

Рис. 1. Динамика пропитки хлопчатобумажной ткани водой, отражаемая в сигналах акустической эмиссии: а — изменение суммы импульсов АЭ; б — изменение амплитуды импульсов АЭ; в, г — осциллограммы и амплитудно-частотная характеристика регистрируемого ультразвукового сигнала: в — начало процесса пропитки, г — продолжение процесса пропитки

а)

По мере пропитывания образца наблюдается отчётливо выраженная динамика изменения всех параметров АЭ. В качестве иллюстрации на рис. 1 представлены типичные данные по изме- нению суммы импульсов, активности АЭ и амплитуды сигналов при пропитке водой ткани с волокнистым составом 100 % хлопка.

Рассмотрим динамику изменения активности сигналов АЭ во времени. Остановимся на общих положениях, основанных на предположении, что количество сигналов АЭ ( N ), индуцируемых при пропитке, пропорционально количеству заполненных жидкостью пор в пропитываемом образце ( M ):

N « f (M)

Соответственно, активность сигналов АЭ dN пропорциональна скорости изменения коли-dt чества пор в пропитываемом образце:

dNdM

= K , dtdt где К — коэффициент пропорциональности.

В начальный момент времени количество пор в образце равно m. В любой момент време- ни (t) количество незаполненных пор равно разности (m -

М )

, а скорость пропитки равна dM .

Предположим, что скорость пропитки пропорциональна текущему значению количества незаполненных пор, т. е. ( m - М ) . Следовательно, мы получим следующее дифференциальное уравнение процесса:

dM

t=k ( m ^- M )

Интегрируя это уравнение, получим решение относительно текущего количества незаполненных пор m - М при начальном условии М = 0, при t = 0:

m - M = me - t ^/T ,                                         (4)

где τ — это постоянная времени релаксации, которая зависит от скорости заполнения пор, а, следовательно, и от вида материала, и от реологических параметров жидкости (вязкости, коэффициента поверхностного натяжения, угла смачивания).

Поскольку в наших проводимых экспериментах мы используем только один вид импрегни-рующей жидкости, а именно — воду, то постоянная времени релаксации τ будет определяться только видом ткани. Она должна быть индивидуальна и постоянна для данного вида ткани вне зависимости от количества индуцируемых сигналов АЭ. Для определения постоянной времени релаксации τ воспользуемся экспериментальными данными по изменению активности АЭ и суммарного счёта при пропитке хлопчатобумажной ткани водой при комнатной температуре.

Используя уравнение (4), мы приходим к уравнению динамики изменения общего (суммарного) количества сигналов АЭ по мере пропитки:

N = Km ( 1 - e ^- t ^/T ) ,                                            (5)

где K — это коэффициент, зависящий от методики регистрации акустических сигналов и чувствительности акустико-эмиссионной аппаратуры, а m — количество пор в образце в начальный момент времени.

Форма кривой, соответствующей уравнению (5), идентична кривой изменения суммарного счёта импульсов АЭ (см. рис. 1 и 2).

С целью определения количественных значений параметров, входящих в уравнение (5), проведена статистическая обработка полученных экспериментальных данных. На приведённых ниже рис. 3. и 4 представлена динамика изменения суммарного счёта сигналов АЭ при пропитке водой образцов ткани с волокнистым составом 100 % хлопка диаметром 80 мм и 200 мм (рис. 4)

соответственно. На этих же графиках показана кривая общего вида y = Km ( 1 - e t ^/т ) с количественными значениями, максимально близко соответствующими экспериментальным данным.

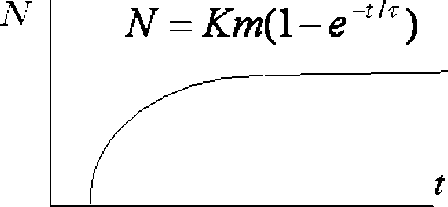
Рис. 2. Форма кривой, описываемой уравнением N = Km ( 1 - e t ^/т

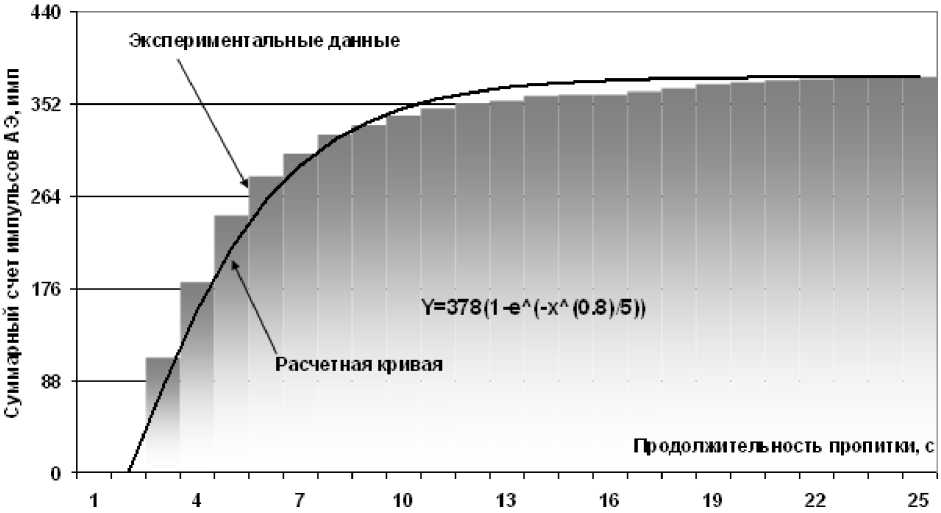
Рис. 3. Изменение суммарного счёта АЭ при пропитке образца хлопчатобумажной ткани диаметром 80 мм

Анализ статистически полученных расчётных кривых свидетельствует, что параметр Km увеличивается с размером пропитываемого образца, что также подтверждает концептуальную правильность уравнения (5). Увеличение размера образца вызывает увеличение числа пропитываемых пор, что и приводит к росту параметра Km . Но наиболее важный результат — это факт неизменности постоянной времени релаксации τ для одного и того же вида импрегнируемого материала — в данном случае ткани с волокнистым составом 100 % хлопка. Именно на этом основывается наблюдаемая внешняя схожесть графиков суммарного счёта импульсов АЭ при пропитке различных по размеру образцов одной и той же ткани. Изменение вида ткани вызывает изменение постоянной времени релаксации τ и, соответственно, наклон кривой суммарного счёта импульсов АЭ.

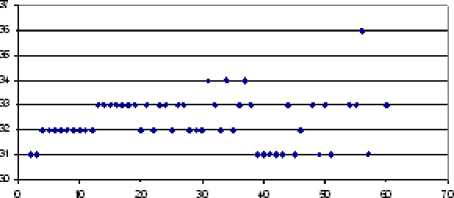
Несмотря на различие в количестве регистрируемых сигналов АЭ при пропитке образцов хлопчатобумажной ткани различного размера, наблюдается одинаковое изменение относительной погрешности метода.

На рис. 5 представлена динамика изменения относительной погрешности в процессе пропитки. Из данного графика становится очевидно, что на заключительной стадии процесса пропит- ки независимо от размера ткани погрешность метода составляет не более 0,3 %. Размер пропитываемой ткани влияет на амплитуду, количество сигналов, но характер изменения активности суммарного счёта для ткани одного и того же вида остаётся неизменным.

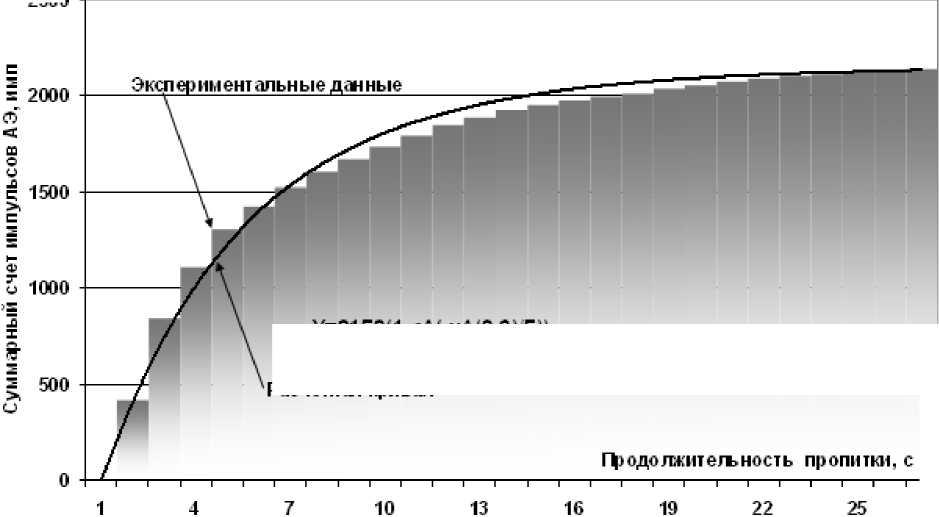
Рис. 4. Изменение суммарного счёта АЭ при пропитке образца хлопчатобумажной ткани диаметром 200 мм

Y=2150(1 -eA(-XA(0.6) 5))

Расчетная кривая

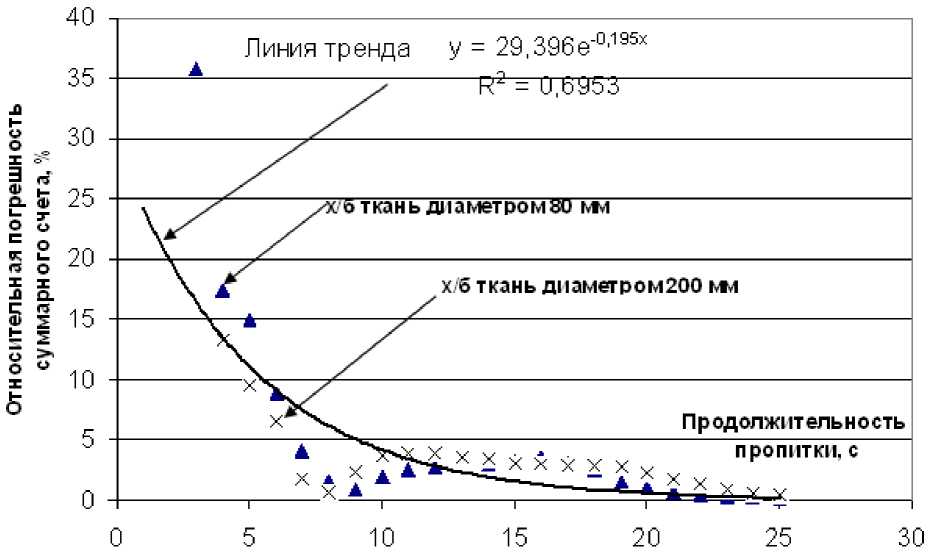
Рис. 5. Изменение относительной погрешности суммарного счёта АЭ при пропитке различных образцов хлопчатобумажной ткани

Выводы. Таким образом, теоретические исследования показывают, что, во-первых, суммарное количество импульсов АЭ при пропитке ткани зависит от количества пор, а, следовательно, раз- мера пропитываемого образца, и, во-вторых, даже незначительное изменение условий пропитки приведёт к изменению как реологии жидкости, так и регистрируемых акустических параметров. Следовательно, для обеспечения воспроизводимости и последующей метрологической оценки метода АЭ применительно к изучению импрегнирования гибких пористых материалов следует проводить измерение в максимально возможных идентичных условиях. Становится очевидным из работы, что метод АЭ в состоянии решить целый ряд проблем, связанных с повышением точности инженерных расчётов конструкций из гибких пористых материалов, подвергающихся механическим деформациям и комплексным теплофизическим, электрическим воздействиям в условиях переменных сред, включая жидкофазные. Исследование явлений диффузии в тканых материалах методом акустической эмиссии позволяет в перспективе создать на его основе метод оценки стабильности различных технических систем в любых жидкофазных средах.