К вопросу о бонитировании березовых древостоев

Автор: Выводцев Н.В., Тютрин С.А.

Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau

Статья в выпуске: 1, 2013 года.

Бесплатный доступ

На основе таблицы хода роста нормальных березовых древостоев обоснована возможность использования в качестве показателя продуктивности среднего прироста по наличному запасу.

Березовый древостой, рост, продуктивность, показатели, наличный запас, средний прирост

Короткий адрес: https://sciup.org/14082691

IDR: 14082691

Текст научной статьи К вопросу о бонитировании березовых древостоев

Совершенствование системы бонитирования насаждений шло по пути создания самостоятельных бо-нитировочных шкал по основным лесообразующим породам [2]. Результатом некоторых из них стали бони-тировочные шкалы на формационном уровне: сосна, ель (Загреев В.В.), лиственница (Выводцев Н.В.) [3], дуб (Дударев А.Д.). Но по существу задачу оценки продуктивности насаждений они не решали.

Цель и методика исследования. Целью исследования является обоснование возможности использования в качестве показателя продуктивности древостоя среднего прироста по наличному запасу.

Для оценки продукционных возможностей древостоя необходимо привлекать наличный запас (Mn). Наличный запас – величина расчетная, трехмерная и в общем виде определяется по формуле (1).

Mn = ∆ср*А = ∑G*HF, (1)

где ∆ср – среднее изменение запаса, м³*га^-1;

А – возраст, лет;

∑G – сумма площадей поперечных сечений (СПС), м²*га^-1;

HF – видовое число, м.

Из формулы (1) следует, что средний прирост соответствует термину продуктивности древостоев, как по физическому смыслу, так и по размерности. Кроме того, анализируя динамику временного изменения среднего прироста из таблиц хода роста (ТХР), можно установить возраст, в котором древостой достигает максимального значения среднего прироста или состояния количественной спелости. Таблицы хода роста нормальных березовых древостоев, составленные Н.Я. Саликовым [2], могут быть использованы как основной норматив для оценки продуктивности березовых древостоев по среднему приросту.

Бонитетные линии высот березовых древостоев получены Н.Я. Саликовым на регрессионной основе [4]. Они отражают характер роста нормальных древостоев в зависимости от условий произрастания в возрастном интервале 10–100 лет. Высота в этом интервале изменяется от 1,2 до 33,4 м. Средний прирост – от 0,3 до 7,9 м3*га-1.

Возможности идентификации продуктивности оценивались по сравнению поведения параметров формулы (1) с изменением класса бонитета. При условии постоянства высоты, с учетом низкой изменчивости видового числа (табл. 1) изменение запаса обусловлено СПС.

Таблица 1

Изменчивость видового числа по ТХР нормальных березовых древостоев Н. Я. Саликова

Высота, м	Класс бонитета						Коэффициент вариации, %
Высота, м	1а	1	2	3	4	5	Коэффициент вариации, %
4	-	-	-	0,570803	0,560595	0,552242	1,7
5	-	-	0,564956	0,552134	0,54314	0,535556	2,3
6	-	-	0,54933	0,537335	0,529282	0,522401	2,2
7	-	0,548989	0,536111	0,525132	0,517842	0,51159	2,8
8	-	0,536778	0,524752	0,514786	0,508132	0,502441	2,6
9	-	0,525939	0,514862	0,505829	0,499719	0,494532	2,5
10	0,531075	0,516308	0,506151	0,497949	0,49231	0,487578	3,2
11	0,521667	0,507734	0,498401	0,490927	0,485704	0,481383	3,0
12	0,513224	0,500077	0,491446	0,484602	0,47975	0,475806	2,8
13	0,505578	0,493209	0,485156	0,478856	0,474337	0,470739	2,7
14	0,4986	0,487013	0,479426	0,473597	0,46938	-	2,4
15	0,492191	0,481384	0,474175	0,468752	0,464812	-	2,3
16	0,48627	0,476229	0,469335	0,464266	0,460579	-	2,2
17	0,480773	0,471466	0,464851	0,46009	0,456638	-	2,1
18	0,475647	0,467023	0,460678	0,456188	-	-	1,8
19	0,470849	0,462843	0,456777	0,452527	-	-	1,7
20	0,466342	0,458878	0,453118	0,449081	-	-	1,6
21	0,462094	0,455092	0,449672	0,445828	-	-	1,6
22	0,458081	0,451461	0,446416	-	-	-	1,3
23	0,454278	0,447972	0,443331	-	-	-	1,2
24	0,450667	0,444623	0,4404	-	-	-	1,2
25	0,44723	0,441427	0,437607	-	-	-	1,1
26	0,443953	0,438403	-	-	-	-	0,9
27	0,440822	0,435586	-	-		-	0,8
28	0,437826	0,433021	-	-	-	-	0,8
29	0,434954	0,430765	-	-	-	-	0,7
Среднее	0,473606	0,474444	0,483188	0,490482	0,495873	0,503427	1,9

Результаты исследования. При равной высоте изменчивость видового числа в нормальных березовых древостоях не превышает 3,2 %. Вместе с тем при увеличении высоты древостоев полнодревесность стволов в насаждениях разных классов бонитета уменьшается и достигает 25%.

Стандартные значения сумм площадей сечений нормальных березовых древостоев из таблиц хода роста Н.Я. Саликова не имеют существенных различий между классами бонитета. Это не позволяет использовать их для оценки продуктивности древостоев. Четкие различия на всем интервале высот показывает динамика среднего прироста по запасу (рис.1). Из рисунка 1 следует, что между средним приростом по запасу и СПС нормальных березовых древостоев связь отсутствует.

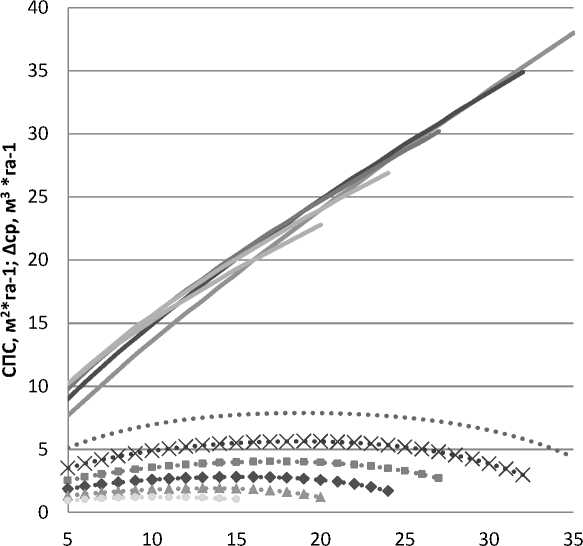
Высота, м

СПС 1а

СПС 1

СПС 2

СПС 3

СПС 4

СПС 5

Δср (1а)

Δср (1)

Δср (2)

Δср (3)

Δср (4)

Δср (5)

Рис. 1. Соотношение среднего прироста и СПС в нормальных березовых древостоях по Н.Я. Саликову

Графический анализ изменения среднего прироста (рис. 2) позволяет сделать следующий вывод: зависимость среднего изменения наличного запаса от класса бонитета имеет линейный вид и выражается через высоту (2).

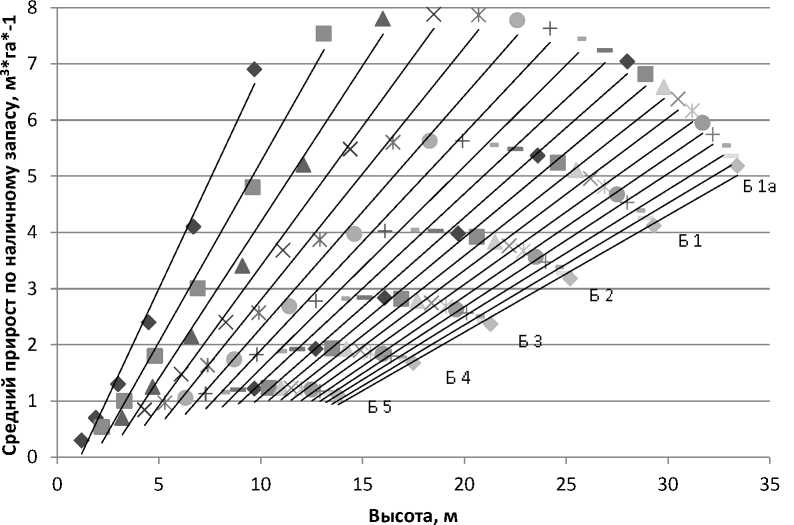
Рис. 2. Зависимость среднего прироста по наличному запаса от условий произрастания

Д ср (Н) = а + ЬН (2)

где ∆ср – средний прирост по наличному запасу, м³*га^-1;

Н – высота, м;

a, b – параметры уравнения.

Анализируя уравнение (2), можно обратить внимание на то, что параметр b характеризует тангенс угла наклона прямой к оси абсцисс. С возрастом влияние условий произрастания на продуктивность березовых древостоев снижается (табл. 2), но не сводится к нулю. Угол наклона прямых говорит об отсутствии в березовых древостоях таких возрастных этапов, для которых характерно влияние на средний прирост только бонитета (угол равен 90 град), равно как и возрастных этапов, когда условия произрастания не оказывают влияния на средний прирост (угол равен 0).

Параметры уравнения (2)

Таблица 2

Возраст	a	b	r
10	-0,87	0,7752	0,995992
15	-1,16	0,6419	0,995892
20	-1,38	0,5563	0,995942
25	-1,57	0,4973	0,996494
30	-1,70	0,4494	0,996293
35	-1,84	0,4138	0,996042
40	-1,94	0,3852	0,996343
45	-2,02	0,3602	0,996143
50	-2,05	0,337	0,996243
55	-2,11	0,319	0,996293
60	-2,13	0,302	0,996444
65	-2,11	0,285	0,996494
70	-2,11	0,2716	0,996343
75	-2,09	0,2582	0,996193
80	-2,09	0,2478	0,996092
85	-2,06	0,2367	0,996343
90	-2,00	0,2253	0,996092
95	-1,98	0,2166	0,995992
100	-1,94	0,2082	0,996193

Примечание: r – коэффициент корреляции.

Для повышения точности аппроксимации зависимости среднего прироста от высоты использовали уравнение параболы второго порядка (3), которое дает высокое приближение экспериментальных данных к теоретическим (табл. 3).

Д ср (Н) = а'+ Ь'Н + с'Н² , (3)

где ∆ср – среднее изменение запаса, м³*га^-1;

Н – высота, м;

a', b', c' – параметры уравнения.

Изменение параметров уравнения (3) в возрастном интервале 10–100 лет приведено таблице 3.

Таблица 3

Возраст, лет	a'	b'	c'	σ	r
10	-0,30662	0,47	0,02851	0,03504	0,99994
15	-0,35895	0,36	0,01867	0,01809	0,99994
20	-0,42043	0,30	0,01343	0,03226	0,99996
25	-0,51983	0,27	0,01005	0,03263	0,99995
30	-0,49048	0,23	0,00863	0,02420	0,99997
35	-0,47893	0,19	0,00771	0,02911	0,99996
40	-0,50859	0,17	0,00674	0,01378	0,99999
45	-0,48968	0,15	0,00620	0,02103	0,99998
50	-0,49433	0,14	0,00552	0,03180	0,99994
55	-0,50550	0,13	0,00510	0,02538	0,99996
60	-0,48997	0,12	0,00474	0,00734	1,00000
65	-0,47241	0,11	0,00438	0,01201	0,99999
70	-0,44373	0,10	0,00417	0,01510	0,99998
75	-0,38723	0,08	0,00402	0,01434	0,99998
80	-0,35225	0,07	0,00391	0,00985	0,99999
85	-0,38181	0,07	0,00361	0,00608	1,00000
90	-0,31353	0,07	0,00350	0,00869	0,99999
95	-0,29363	0,06	0,00338	0,01187	0,99998
100	-0,30806	0,06	0,00318	0,00400	1,00000

Примечание: σ – стандартная ошибка, r – коэффициент корреляции.

Параметры уравнения (3)

Визуальный и графический анализ параметров уравнения (3), свидетельствует о том, что они подчиняются определенным закономерностям, которые могут быть переданы конкретными функциями, представленными в таблице 4.

Функции аппроксимации параметров уравнения (3)

Таблица 4

Параметр уравнения (3)	Функция аппрокимации	Показатель точности		Параметр
Параметр уравнения (3)	Функция аппрокимации	σ	r	a	b	c	d	e
a'	f(A)=a+bA+cA^2+..+dA^4	0,025	0,962	-0,132	-0,021	0,00034	-1,5*10^-6	8,6*10^-11
b'	f(A)=a(b^A)(A^c)	0,006	0,999	1,493	0,988	-0,452	-	-
c'	f(A)=a(b^A)(A^c)	0,0002	0,999	0,406	1,006	-1,180	-	-

Примечание: A – возраст, лет; σ – стандартная ошибка, r – коэффициент корреляции.

Подставив значения параметров функций аппроксимации в уравнение (3), получили математическую модель зависимости среднего прироста от возраста и высоты в нормальных березовых древостоях (4).

Дср(Н, Л) = [-0,132 - 0,021 * А + 0,00034 * Л² - 1,5 * 10^-6 * A 3 + 8,6 * 10^-11 * Л⁴] +

[1,493 * 0,988^л * Л^-0 , ⁴⁵²] * Н + [0,406 * 1,006^л * Л^-1 , ¹⁸⁰] * Н 2 , (4)

где ∆ср – среднее изменение запаса, м³*га^-1;

А – возраст, лет;

Н – высота, м.

Ограничения уравнения (4) опосредованы ТХР нормальных березовых древостоев Н.Я. Саликова: 10 ≤ А ≤ 100; при 1,2 ≤ Н ≤ 33,4.

Систематическая ошибка по данным 114 точек измерения составила 0,005 м3*га-1, среднеквадратическая ± 0,029 м3*га-1 при точности 95% (табл. 5).

Статистики распределения ошибок модели (4)

Таблица 5

Среднее	-0,005
Стандартная ошибка	0,003
Медиана	-0,007
Стандартное отклонение	0,029
Дисперсия выборки	0,001
Эксцесс	0,039
Асимметричность	-0,137
Интервал	0,144
Минимум	-0,081
Максимум	0,064
Сумма	-0,613
Счет	114

Распределение погрешностей аппроксимации на исходном материале показало, что точность определения среднего прироста по разработанной модели (4) не зависит от возраста и класса бонитета (рис. 3).

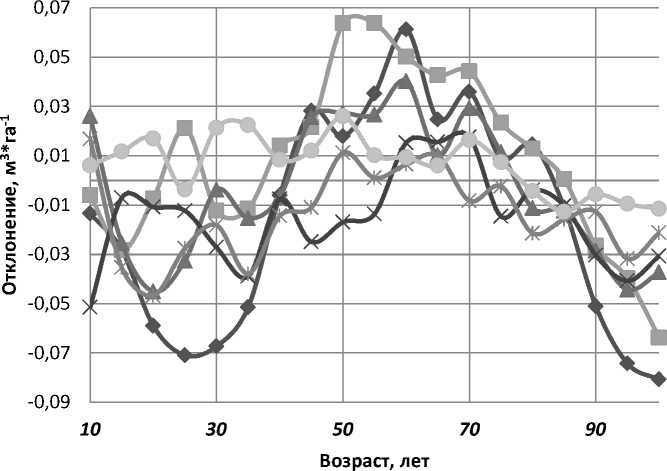
1а

Рис. 3. Анализ абсолютных ошибок модели (4)

Параметры ( H, A) входят в состав бонитировочной шкалы М.М. Орлова. Табулированием уравнения (4) получили бонитировочную шкалу М.М. Орлова, сопряженную со средним приростом по запасу стволовой части (табл. 6).

Таблица 6

Средний прирост в березовых древостоях в зависимости от возраста и класса бонитета

Возраст, лет	Класс бонитета
Возраст, лет	1а	1	2	3	4	5
10	2,85692	2,23018	1,64469	1,10046	0,59748	0,13577
15	3,49953	2,75078	2,02671	1,35968	0,77298	0,21772
20	3,97701	3,12155	2,33050	1,58148	0,90109	0,30740
25	4,37288	3,41990	2,54363	1,76411	1,05732	0,40711
30	4,64035	3,64662	2,75486	1,92260	1,17203	0,51777
35	4,83218	3,82049	2,89271	2,04884	1,28888	0,61284
40	4,98549	3,95391	3,00937	2,15189	1,38145	0,69806
45	5,06817	4,01885	3,07701	2,22277	1,45611	0,77705
50	5,11067	4,07897	3,13616	2,26806	1,50459	0,83001
55	5,13684	4,10241	3,15876	2,30589	1,54379	0,87247
60	5,14865	4,12572	3,17871	2,32484	1,56413	0,89657
65	5,14742	4,11848	3,18258	2,33974	1,57914	0,92384
70	5,14993	4,11284	3,18512	2,35084	1,60999	0,96257
75	5,13957	4,12198	3,19861	2,36944	1,63449	0,99375
80	5,13153	4,13007	3,20897	2,38320	1,66241	1,03428
85	5,10994	4,10975	3,21565	2,41309	1,70207	1,08260
90	5,08876	4,11380	3,22961	2,43617	1,72439	1,10590
95	5,06655	4,08877	3,21511	2,43174	1,73865	1,13584
100	5,01479	4,05992	3,19511	2,42037	1,73569	1,14108

Примечание: жирным выделен максимальный средний прирост.

Заключение. Таким образом, на основе ТХР нормальных березовых древостоев Н.Я. Саликова получена математическая модель бонитеровочной шкалы М.М. Орлова, в которой зависимой переменной является средний прирост, а независимыми переменными возраст и высота. Ее математическое выражение позволяет в автоматическом режиме устанавливать продуктивность древостоев. Модель может найти практическое применение при оценке степени нормальности древостоя. Например: установлено, что березовый древостой к 45-летнему возрасту достиг высоты 17,4 м (1 класс бонитета по шкале М.М. Орлова). По уравнению (4) средний прирост данного древостоя в 45 лет составляет 4,02 м³*га^-1. В этом же возрасте и классе бонитета по ТХР нормальных березовых древостоев Н.Я. Саликова средний прирост равен 5,6 м³*га^-1. По отношению средних приростов дается оценка, согласно которой рассматриваемый древостой по продуктивности соответствует нормальному на 72 %.

Статья научная