К вопросу о количестве разрешенных кодовых комбинаций в кодах с исправлением ошибок

К орректирующие коды с исправлением ошибок при приеме символов кодовой комбинации, известные нам также как избыточные или помехозащищенные, получили широкое применение в системах связи. Применение корректирующих кодов считается одним из эффективных способов повышения достоверности приема двоичной информации. Однако использование корректирующих кодов ограничено системами, в которых посылка информационного сигнала известна априори с вероятностью 1,0, а аппаратура на приемной стороне обслуживается человеком. В таких системах единственным критерием и показателем помехоустойчивости служит вероятность ошибочного приема символа двоичной комбинации (вероятность ошибки на символ), зависящая от отношения сигнал/шум в полосе фильтра, согласованного с символом.

В линейных (систематических) корректирующих кодах с исправлением S ошибок кодовая комбинация, состоящая из n разрядов, содержит k информационных и r контрольных (проверочных) символов так, что n = k + r .

Информационные и контрольные символы в кодовой комбинации располагаются в строго определенных местах. В частности, в циклических кодах первые k символов являются информационными, а остальные символы – контрольными. Такие коды обозначаются (n, k) .

Общее количество кодовых комбинаций равно

N = 2n .                                                (1)

Из них количество разрешенных кодовых комбинаций (емкость кода) составляет

M = 2k = 2n-r = 2n/2r.                              (2)

В корректирующих кодах с исправлением ошибок кодовое расстояние (минимальное количество символов, которыми одна кодовая комбинация отличается от другой) связано с числом исправляемых ошибок S соотношением d = 2S + 1.                                              (3)

К сожалению, вопрос об определении минимального числа избыточных символов для построения кода с исправлением ошибок до настоящего времени не решен, существует лишь ряд верхних и нижних оценок границы этой области.

Наиболее известны оценки Хэмминга и Варшамова–Гиль-берта. Если оценка Хэмминга в литературе трактуется однозначно, то относительно оценки Варшамова–Гильберта в литературе имеются определенные неточности и противоречивые соотношения.

Материал, рассмотренный далее, представляется в целях устранения указанных неточностей и противоречий.

Оценка Хэмминга для избыточных символов имеет вид ошибки в комбинации может быть любое. Распределение числа ошибок s как случайная величина подчиняется биноминальному закону

^=с:рг(1-р,у,

где Р_э - вероятность приема символа.

При отсутствии сигнала в симметричных каналах связи Р_э = 0,5 . Тогда средняя частота ложного приема кодовой комбинации на каждом тактовом интервале, равном длительности кодовой комбинации Т_к , будет определяться выражением

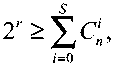
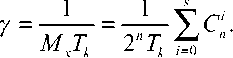
где

- число сочетаний из n по i , равное

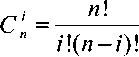
Подставляя (4) в (2), определим количество разрешенных кодовых комбинаций

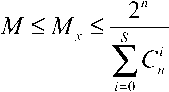
Выражение (5) в литературе известно как верхняя граница Хемминга для количества разрешенных кодовых комбинаций. Неравенство (5) переходит в равенство для совершенных (или так называемых плотно упакованных) кодов.

Верхняя граница Хэмминга используется и в операциях над простыми кодами. В частности, вероятность ложного приема n -разрядной двоичной комбинации под действием случайных или воспроизводящих помех.

Ложный прием кодовой комбинации представляет собой случайное событие. Вероятность того, что за время T_a произойдет ровно К таких событий, определяется законом Пуассона

, JyT^ Та

w к! ’

При условии γТа<<1,0 , можно воспользоваться первыми двумя членами разложения в степенной ряд (8). В результате получим

1;,гтт..

Формулами (8) и (11) можно пользоваться, когда ни одна из разрешенных кодовых комбинаций не обнаруживается и не расшифрована.

Оценка Варшамова–Гильберта устанавливает нижние границы для количества разрешенных кодовых комбинаций.

В [2, 5, 6] даны следующие выражения для количества избыточных символов

IS

Y^TC‘(12)

25-1

2z >lc:?(13)

^>1^(14)

i=0

Соответственно получаем нижние границы Варшамова– Гильберта для количества разрешенных кодовых комбинаций где γ - средняя частота событий (ложных приемов).

Использование пуассоновского закона в данном случае оправдывается тем, что отсутствует последействие и имеет место ординарность.

При к = 0 имеем

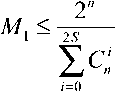
э _ с-Л

(A') J '

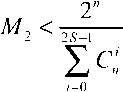
Вероятность того, что за время Т_а произойдет хотя бы одно событие будет равна

р = Р ^1-5-/Т

(Л)    1(к>\}    1 а •

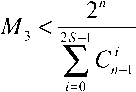
Кодовая комбинация считается принятой правильно при правильном приеме не менее n - s символов из n , т.е. допускается не более s ошибок в приеме символов, причем место

Очевидно, что эти границы здесь располагаются в возрастающем порядке, т.е. мы имеем M₁< M₂< M₃ .

Отметим, что в [1, 3, 4] неравенства (12) – (14) и (15) - (17) приведены ошибочно с противоположным знаком.

Реально количество разрешенных комбинаций М будет находиться в промежутке между одной из границ Варшамо-ва–Гильберта и верхней границей Хэмминга. Выбор нижней границы Варшамова–Гильберта зависит от количества избыточных символов и числа исправляемых ошибок S . При малой избыточности и небольшом числе исправляемых ошибок количество разрешенных комбинаций M будет находиться в промежутке: M₃< M < M_x .

Указанные выше соотношения могут быть подтверждены несложным экспериментом. Сформируем на ЭВМ случайную двоичную комбинацию с разрядностью n = 12 . Предположим, что исправляется S = 2 ошибки в приеме символов двоичной комбинации, следовательно, в соответствии с (3) кодовое расстояние будет равно d = 5 . Путем сложения по модулю 2 каждой из 2¹²=4096 комбинаций со всеми ос-таль-ными определим количество кодовых комбинаций, отличающихся друг от друга не менее чем на d = 5 символами. Это число, совпадающее с количеством разрешенных кодовых комбинаций, в нашем примере составляет М = 26 .

Верхняя граница Хэмминга в нашем примере в соответствии с (5) равна М_x = 51,85 , а нижняя граница Варшамова-Гиль-берта в соответствии с (17) составят М₃ = 17,65 .

Таким образом, количество разрешенных комбинаций в нашем примере находится в промежутке между М_х и М₃ .

Заметим что в нашем примере также имеем М₁ = 5,16 и М₂ = 13, 7. Использование их для определения области разрешенных кодовых комбинаций означало бы более осторожную оценку.

Нижняя граница Варшамова–Гильберта, как и верхняя граница Хэмминга, могут быть использованы в операциях над простыми кодами, в частности, при оценке вероятности вос- произведения сигнала после обнаружения и расшифровки одной из разрешенных кодовых комбинаций из общего ансамбля. В этом случае средняя частота ложного приема сигнала будет определяться по формуле

1 ад

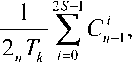
а вероятность ложного приема найдем после подстановки (18) в (8).

Выводы

• 1.    Верхняя граница Хэмминга и одна из нижних границ Варшамова–Гильберта, ограничивающие область разрешенных кодовых комбинаций в кодах с исправлением ошибок, могут быть использованы и в операциях над простыми кодами.

• 2.    Верхняя граница Хэмминга используется при оценке вероятности ложного приема двоичного сигнала под действием случайных и воспроизводящих помех в условиях, когда ни одна кодовая комбинация из общего ансамбля сигналов не обнаружена и не расшифрована.

• 3.    Нижняя граница Варшамова-Гильберта может быть использована при теоретической оценке вероятности воспроизведения двоичного сигнала после обнаружения и расшифровки одной из разрешенных кодовых комбинаций из общего ансамбля.

• 4.    Устранены противоречия в некоторых литературных источниках [1, 3, 4], касающиеся знаков неравенств для границ Варшамова-Гильберта.