К вопросу о повышении качественных характеристик усилителя мощности в ключевом режиме с последовательным контуром

Ключевой усилитель с последовательным контуром (рис. 1) по существу представляет собой разновидность схемы инвертора, применяемого в силовой преобразовательной технике. Главное его достоинство – высокий КПД, достигающий 90…95 %. Однако реализовать это достоинство удается лишь на сравнительно низких частотах (до 150…200 МГц в транзисторном варианте). Кроме того, при работе в полосе частот требуется перестройка колебательной системы, что осложняет конструкцию усилителя и снижает его надежность. Предлагаемый ниже анализ рассматриваемой схемы позволяет сделать выводы о допустимых пределах расстройки колебательной системы для приемлемых значений энергетических показателей усилителя.

Эквивалентная схема усилителя. Один из вариантов схемы инвертора с последовательным контуром приведен на рис. 1, а . Непосредственный анализ этой схемы затруднен, так как она может быть описана дифференциальным уравнением не ниже третьего порядка. Задачу можно упростить при следующих условиях:

– резонансная частота последовательного контура ω 0 близка к частоте возбуждения (переключения) ω;

– затухание контура L _к C _к R _н достаточно мало:

R н      « 1;                 (1)

– внутреннее сопротивление транзистора для мгновенных значений анодного тока (в открытом состоянии) по крайней мере не больше сопротивления нагрузки R н :

R <  R н ;                     (2)

– напряжение возбуждения имеет форму меандра.

При этих условиях Z н ≈ R н /cosφ; транзисторы можно заменить эквивалентными ключами с потерями, а последовательный контур усилителем тока имеет синусоидальную форму i = I sin(m t + ф), где ф - фазовый сдвиг контурного тока, обусловленный расстройкой.

В результате усилитель может быть представлен эквивалентной схемой (рис. 1, б), где С0 – выходная емкость транзистора.

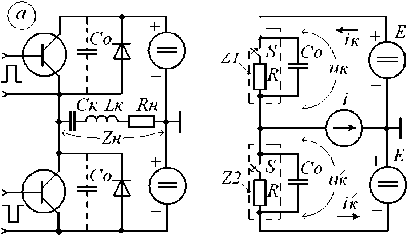
а                          б

Рис. 1. Схема усилителя с последовательным контуром

Амплитуду возбуждения выберем такой, чтобы в открытом состоянии сопротивление транзистора было минимальным, т. е. определялось линией критического режима (или сопротивлением насыщения):

R = —- = r ,

нас , Sкр где Sкр – крутизна линии критического режима.

Поскольку переключение цепей осуществляется ключами поочередно, то для полных сопротивлений ключей Z можно записать следующие выражения:

Здесь и в предшествующих двух выражениях

Ф n = arctg ( 2 n - 1 ) 2 m RC 0 .

где Sq ю t = -

или

Z 1 =    ² R   ,

1 - Sq tot

2 R , 1 + Sq ю t

T

2 ^,

- 1 ^ ( 2 n + 1 )- < t < ( n + 1 ) T ,

4   sin ( 2 n - 1 ) ю t

Sq ю t =-£^— r-

^П n =1     ² n ^{- 1}

.

С учетом принятых обозначений (4) и (5), эквивалентную схему (см. рис. 1, б ), можно описать линейным неоднородным дифференциальным уравнением следующего вида:

du 1

+UK dt   2RС0 к или с учетом (6)

—^E — (1 + Sq ю t )--—sin(ю t + ф),

2 RС ₀           2 С ₀

du 1

—к" +-----uK dt 2RС0 к

E 2 RС ₀

4 ^ sin ( 2 n - 1 ) ю t ^{1+ n} n =1    ^{2 n - 1}

- T-;rsin(to t + ф), 2 С ₀

Периодическое решение этого уравнения нетрудно найти методами гармонического синтеза [1]:

U к ( t ) = 2 E

T

t

—

2 RC 0

1----

1 + e ^{4 RC} 0

IR sin(ю t - ф 1 +ф ) 7 1 + (2 m RC 0 )² ’

T на интервале nT < t < (2n +1) —, и

t

, в 2 Ee ^{2 RC 0} IR sin( m t -ф +ф )

^U к ⁽ t )=--------- г--- 1             ¹₂

1 ₊ e - 5 RC    V1 + (2m RC 0 )²

T на интервале (2Т +1) — < t <( n + 1) T.

Это же решение Фурье:

можно записать в виде

ряда

, в              4 ”

u к (t )=EI1+-E n n=1

sin [ ( 2 n - 1 ) m t -ф n

( 2 n - 1 ) 7 1 + [2 m RC 0 (2 n - 1)]²

-

IR sin( m t -ф 1 + ф )

71 + (2 m RC о )²

,

Выражение (10) позволяет найти амплитуду напряжения первой гармоники.

Полагая, что IR ^ E , получим

Г 4 E ™

U 1 ® I-- IR cos ф

I л

J 1 + (2 m RC о )² "

Форму импульса тока можно определить следующим выражением:

i = ^U к ⁽ t )

к     _{Z 1}

.

T

Тогда на интервале nT <  t < ( 2 n + 1 ) -2, i _к = 0, и

t

2 Ee 2 RC 0

к

T

R 1 + e ^{4RC 0}

sin( m t -ф 1 +ф ) 71 + (2 m RC 0 )² ’

на интервале (2 n + 1) T 2 < t < ( n + 1) T .

Основные энергетические соотношения в ключевом усилителе. Ограничимся рассмотрением области малых значений φ₁ в (11):

Ф 1 = arctg2 m C 0 R <  10 ° , 2 m RC 0 « 1, ф 1 ® 2 m C 0 R . (13)

Как будет показано ниже, уже в этой области происходит существенное ухудшение энергетических показателей ключевого усилителя.

С учетом (13) можно приближенно определить амплитуду контурного тока:

r 4 E

I = и н . U.     ⁿ

Z н Z н

- IR cos ф I cos ф

R н

,

или после приведения подобных членов

I = ,     ⁴ E_____

I              R.

n| R cos ф + —— (         cos ф

.

Определим постоянную составляющую основании (12) и (15):

1 ”

I к о = nJ

^{2 П} о

t

2 Ee ^{2 RC 0}

R 1 + e

T 4 RC 0

4 E sin( m t -ф 1 + ф )

Г „ . R n| R cos ф+— ( cos ф

После простых преобразований получим

тока на

d m t .

пю RC ₀ 1 - e

Л

2 ю RC о

R н R

I = 4 E <  к⁰ п²R ‘

Л —

2 1 + e ^{2ю RC 0}

+

,

+

cos( ф-ф ₁)

[ 1 + (2 ю RC ₀)² JI cos ф +

или, принимая во внимание (13),

cosф +

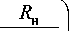
R cos ф J

cos( ф-ф ₁) +

пюRC f—2—01 cosф+

R cos фJ

Рассмотрим вариант настройки контура в резонанс (φ = 0; ω = ω 0 ). В этом случае (20) с учетом (13) примет вид

П(юо) —

R н

R

4E ко „.2

π R

nm RC 0    cos(ф - ф 1 )

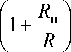
4фИ1 R_H cos ф₁ + ¹ 1 + н

¹ п I R

R cosф +--н—

R cosφ

.

Мощность, потребляемая от источника питания одним транзистором,

^P 0 = ^EI к о

4 E ² п ² R

пю RC 0     cos( ф - ф 1 )

R

COS ф +-- н

R cos ф J

. (17)

Для колебательной мощности, отдаваемым одним транзистором в нагрузку, на основании (15) получим следующее выражение:

P- 1 f I 2 R H

Р 1 —

¹ 2 1 2

4 E ^{2 н} R

₂ J R

п RI cosф^--н—

( R cos ф

2 ,

Семейство зависимостей (21) приведено на рис. 2.

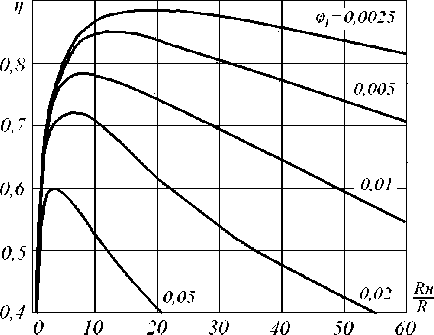
Рис. 2. Нагрузочные характеристики усилителя

а затем определим мощность потерь на транзисторе:

4 E ²

a

п R

cos( ф-ф 1 )

COS ф +    н—

R cos ф

R н

R + ^{пю RC} о r Л ²     2

.

Два первых слагаемых в (19) характеризуют потери на транзисторе, обусловленные протеканием контурного тока i . Третье слагаемое учитывает потери, вызванные разрядным током выходной емкости лампы. Наличие именно этого слагаемого приводит к увеличению потерь и уменьшению КПД на повышенных частотах.

Выражения (17) и (18) позволяют определить электронный КПД усилителя:

P 1

n —F —r P0

R н R

пю RC 0 , cos( ф-ф ₁ )

2 +      R^T cosф+   н—

R cos ф

cosф +

R

R cos ф

Из (21) следует, что каждому значению φ 1 соответствует определенное оптимальное значение сопротивления нагрузки R н , которое можно найти путем исследования (21) на экстремум:

f Ra.

I R

opt

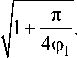
Выражение (21) подтверждает справедливость ограничения области рассматриваемых значений φ 1 . Действительно, уже при φ 1 = 3° (0,05 рад) максимально возможное значение КПД не превышает 0,6.

Рассмотрим теперь зависимость энергетических показателей усилителя от расстройки нагрузочной цепи . Для этого в дальнейшем воспользуемся понятием обобщенной расстройки [2]:

f ю ю0 J     fю-ю0 J

X — tg ф — I---⁰ I Q ® 21-----⁰ I Q ,

l ю0 ю J l юо J

где Q – нагруженная добротность контура.

Предположим, что в пределах рабочей полосы усилителя допустимо снижение КПД до k· η(ω 0 ) и рассмотрим зависимость энергетических показателей усилителя от расстройки нагрузочной цепи при оптимальном сопротивлении нагрузки.

Выражение (21) в этом случае примет вид

k ■ n (®0)

R н R

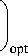
Г R н ^

COSф + l — I

V R ⁾ opt

cos ф

^cos (< p ф 1 ) ⁺ -ф₁ ^cos ф ⁺ l — I--

П ¹ V R ) opt ^cos ф

С учетом (23) это выражение можно решить в виде χ доп = tg(φ доп ) = f (φ 1 , k ), где χ доп и φ доп – допустимые значения обобщенной расстройки и фазового сдвига контурного тока при фиксированном φ 1 и заданной величине снижения КПД ( k ).

Результаты этого решения представлены на рис. 3.

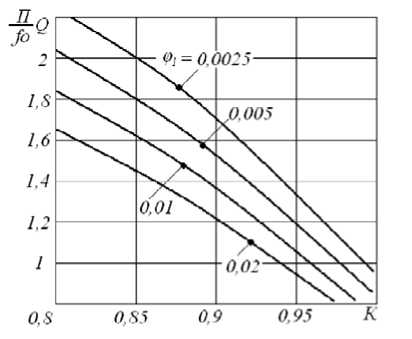
Рис. 3. Полоса рабочих частот усилителя: П = 0,5(χ 1 + χ 2 ); χ 1 = χ(ω доп – ω 0 ) … ω > ω 0 ; χ 2 = χ(ω 0 – ω доп ) … ω < ω 0

Таким образом, можно сделать следующие выводы:

– на умеренно высоких частотах (φ = 0,0025 – – 0,005) при допустимом снижении КПД на 20 % полоса рабочих частот усилителя может достигать удвоенной полосы пропускания контура на уровне 3 дБ;

– на высоких частотах (φ > 0,01) падает и резонансное значение КПД и допустимая полоса рабочих частот;

– рабочую полосу частот можно регулировать подбором нагруженной добротности контура.