К вопросу о применении тестирования по математике у студентов, обучающихся по направлению подготовки «управление персоналом», в рамках компетентностного подхода

Современный ФГОС ВПО требует придерживаться компетентностного подхода в обучении студентов, то есть критерием качества обучения служит овладение студентами рядом общих и профессиональных компетенций. В то же время качество работы вуза в целом и каждого преподавателя в частности оценивается на базе тестирования студентов по преподаваемым дисциплинам. В настоящей статье мы на конкретных примерах постараемся показать противоречие меж- ду необходимостью формирования у студентов профессиональных компетенций и необходимостью готовить (или даже, как часто формулируют, «натаскивать») студентов к выполнению тестовых заданий. Действительно, в реальной профессиональной деятельности никому и никогда не ставятся вопросы в виде тестов. В жизни мы имеем дело с проблемными ситуациями, в которых необходимо принимать решение, и эти ситуации требуют, как анализа имеющихся факторов, так и прогнозирования возможных последствий принимаемых решений, но никакая ситуация не предлагает выбор из 4 вариантов ответа, которые предложены кем-то заранее. Существующая система оценивания работы студентов и преподавателя с помощью тестов, с нашей точки зрения, ставит преподавателя перед весьма затруднительным выбором: либо потратить время на обучение студентов тому, что им действительно будет полезно, но не имеет никакого отношения к тестам, либо обезопасить себя и потратить бесценное время (которого, как правило, и так даётся программой слишком мало) на прохождение со студентами тренировочных тестовых заданий. В настоящей статье нам хотелось бы наглядно показать, как система тестирования может приводить к перекосам, когда обучение выполнению тестовых заданий может легко и очень далеко увести от понимания сути решаемых задач, т. е. препятствовать формированию реальных, а не абстрактных профессиональных компетенций. Все приводимые в примерах задания взяты из демонстрационных вариантов открытого сегмента единого портала интернет-те-стирования в сфере образования www.i-exam.ru [1, 2].

Пример 1.

Транспортная задача

120 200 С 300 10 15 18 а 17 10 5 b 4 20 10 будет открытой, если,

Варианты ответа а =100 , b=100 , с = 180

а = 200, Ь=140, с = 320

а =150 , Ь=150 , с = 320

а = 32 , b = 34 , с = 46

При решении транспортных задач, вне всякого сомнения, имеет значение умение понимать, является ли задача открытой (так как в таких случаях необходимо вводить фиктивного поставщика или потребителя) или закрытой (замкнутой [3, с. 86]). Однако можно отметить, что для этого отнюдь не требуется знание данной терминологии, тем более, что в ряде источников, например [4, c. 44], [5, c. 181], [6, c. 7], вместо этих терминов используются понятия сбалансированная (синоним закрытой) и несбалансированная (синоним открытой) задачи, что имеет более наглядный и понятный экономический смысл, а в некоторых работах используются термины «задача с правильным балансом» и «задача с неправильным балансом» [7, с. 78]. Таким образом, студент, отлично решающий транспортные задачи, может не справится с заданием только из-за того, что не знает термина, так как занимался по учебному пособию, в котором этот термин нигде не встречается, например [5, 7].

Более серьезным, на наш взгляд, недостатком является то, что студент, который абсолютно не умеет решать транспортные задачи (а их решение требует нахождение опорного плана одним из многих возможных методов, проверки этого плана на оптимальность и построения улучшенного решения), может легко справится с данной задачей, если будет научен преподавателем единственному факту: задача является закрытой, если сумма запасов равна сумме запросов, и открытой, если эти суммы не равны. Конечно, тут требуется понять, где в таблице находятся запасы, а где запросы, но этого-то как раз и нельзя сделать исходя из таблицы, приводимой в тесте, так как в ней отсутствуют подписи! То же можно сказать и еще проще — сложите числа в первой строке и в первом столбце — и если они совпадут, то задача закрытая, а нет — открытая. Конечно, расположение столбцов заказов и запасов можно поменять. Например, во многих учебных пособиях ([3, c.90-93], [6, с. 12], [7, c. 74-76]) расположение данных в таблице с подписями выглядит приблизительно так:

Склады /	Транспортные издержки			Запасы
потребители	Р 1	Р 2      …	Р n
S 1	c 11	c 12     …	c 1n	a1
S 2	c 21	c 22     …	c 2n	a2
S … m	c m1	…… c m2    …	c mn	am
Заказы	b 1	B 2      …	b n

То есть заказы и запросы расположены не в первых строке и столбце, а в последних. Для овладения же навыком решать транспортные задачи в практических ситуациях нет совершенно никакой нужды знать, что таблицы можно составлять по-разному, а важно уметь составлять их самому на основании реальных данных в любой удобной форме. Поэтому, для успешного прохождения тестов преподаватель вынужден рассматривать различные формы записи и тратить на это время, вместо того, чтобы учить проходить все шаги решения транспортной задачи в одной выбранной форме записи. В то же время не составляет особого труда «натаскать» студентов на нахождение стро- чек и столбцов, суммы в которых нужно сравнивать. Достаточно, например, объяснить, что это те строчка и столбец, находящиеся с краю, в которых имеется «необычная» клетка (пустая, либо с подписями).

Пример 2. Область допустимых решений задачи линейного программирования имеет вид:

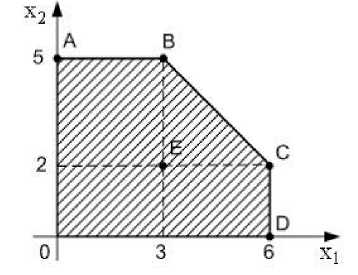
Тогда максимальное значение функции F(x) = x1 + 2x2 равно …

Варианты ответов: 11, 7, 13, 10.

Приведенная задача относится к теме «линейное программирование». Задачи по данной теме носят практический характер, чрезвычайно важны для формирования у экономистов и менеджеров профессиональных компетенций, умения оптимально планировать деятельность, принимать рациональные и экономически выгодные решения. Основной сложностью при решении таких задач является выработка у студентов умения грамотно построить математическую модель, то есть представить практическую ситуацию в виде набора математических выражений. Наработка технических навыков по решению задач в математической форме является в современных условиях задачей второстепенной, так как существует целый ряд взаимозаменяющих методов решения таких задач, в том числе и с применением современных компьютерных технологий [4, c. 56-59], [8, с. 12-13]. В приведенном же выше примере предполагается, что задача должна быть решена графически. Но возникает вопрос, а стоит ли учить студентов-менеджеров графическому методу, если он не является универсальным, а подходит лишь для очень узкого круга задач с двумя переменными (в то время как большинство практических экономических ситуаций имеют дела с гораздо большим числом переменных) и существует универсальный симплекс-метод решения таких задач, подходящий как для двухмерного, так и для многомерного случая, а также удобный для компьютерной реализации? Так что вновь преподаватель математики сталкивается с дилеммой: либо отрабатывать составление многомерных моделей и решение их на компьютере (допустим хотя бы средствами стандартной офисной программы Excel), либо тратить время на отработку графического метода. И вновь задача дает возможность недобросовестному злоупотреблению. Можно сообщить студентам, что максимум и минимум достигается всегда в вершине многоугольника и натренировать студентов подставлять координаты всех вершин многоугольника в целевую функцию, находя наибольшие и наименьшие значении.

Можно даже подставлять не все вершины, а заметить, что в данном примере из предложенных вариантов максимальным является 13, а этот вариант достигается в вершине В, поэтому дальше проверять уже нет смысла — это и есть правильный ответ, т. к. остальные предложенные варианты уже заведомо будут меньше. Не спасает и следующая формулировка, также имеющаяся в базе тестовых заданий:

Пример 3:

Минимальное значение целевой функции Варианты ответа F(x) = — xj — 3x2 ПРИ ограничениях

1хг + х2 210,° ”

Х2 2 8,о _ х2 —

О -30 х2 2 0, х2 2 О, равно...О —26

Для решения такой задачи можно либо обучить студентов строить графические изображения допустимых множеств, что уже не мало, либо поступить еще проще: можно сказать, что вершины будут получаться, если мы заменим неравенства на равенства и будем решать их парами, проверяя получаемые результаты подстановкой в остальные неравенства (результаты, которые не подходят, отбрасываем). Например, пара

{ X_t + X, -10

х2 = 8

дает вершину (2, 8) в ней F(x) = –26; решая систему

) Х₁^{+ Х}2 ⁼ 1 О

Xi — 2

получаем (8, 2), F(x) = –14, что больше, чем — 26, и не является минимальным значением. Система

{ x_t + х, -10

Xj = О дает пару (0, 10), которая не подходит во второе неравенство. Используя в качестве второго уравнения х2 = 0, получим точку (10, 0), F(x) = –10, что еще больше. Аналогично проверяем точки (0, 8): F(x) = –24 и (0,2): F(x) = –6 и получаем, что минимальным значением является –26.

Решая данную задачу, можно рассуждать так: в целевой функции оба коэффициента даны с минусом, т. е. чем больше будут значения переменных, тем меньше будет функция. Исходя из второго неравенства х2 не больше 8 (если брать меньше, то функция увеличится), подставим х2 = 8 в первое уравнение х1 + х2 = 10, получим х1 = 2. Значения х1 = 2 и х2 = 8 подходят во все неравенства системы, значение целевой функции в точке (2, 8) равно — 26. выбираем данный ответ. Данное решение приводит к правильному результату во многих аналогичных ситуациях, хотя рассуждение, в общем-то, является некорректным (например, если за счет уменьшения х2 можно существенно увеличить слагаемое с х1), и для большего числа перемен- ных можно, рассуждая аналогичным образом, прийти к совершенно неверному результату. Система тестирования совершенно этого не учитывает.

Отметим, что, по нашему мнению положение не спасет и замена графического метода на любой другой метод (тот же симплекс-метод в его технической реализации имеет слишком много вариаций, чтобы настаивать на изучении какого-то одного). Единственным выходом является проверка умений студентов оперировать с реальными ситуациями, но для этого нужно, чтобы проверочная работа состоял из одной-двух задач, на решение которой отводится достаточно времени, и чтобы проверялись все шаги решения. Метод же студент имеет право выбирать самостоятельно, главное, чтобы решение было верным и достаточно обоснованным (не только получен правильный ответ, но и была гарантия, что он наилучший).

Пример 4.

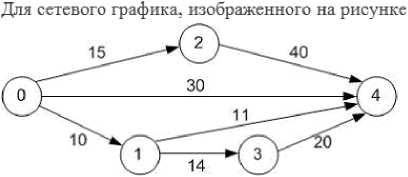
критической является работа ...

Варианты ответа: (0, 4), (1, 4), (2, 4), (3, 4).

Задачи по составлению сетевых графиков являются важными и полезными для специалистов по управлению — они позволяют грамотно составлять план работ и контролировать ход их выполнений с тем, чтобы не происходило сбоев в сроках сдачи проектов. Задача по составлению сетевого графа — творческая и сложная, требует соблюдения ряда правил, важным моментом является упрощение сложных графов (подробнее с такими задачами можно ознакомится в работах [3, c. 133-151], [4, 101-111]. Ничему из вышеперечисленного нельзя научить студента, если решать с ним только задачи с готовыми графами (хотя они, безусловно, полезны как тренировочные на начальном этапе, но обучение их решению не является самостоятельной целью — практические ситуации не содержат готовых графов, их необходимо уметь составлять самому). При тестировании же умение составлять граф не учитывается, а у преподавателя опять возникает соблазн больше времени потратить на решение задач по готовым графам, чем на их составление. В результате студенты хорошо справляются с тестовыми заданиями и приобретают навык, который практически оказывается совершенно бесполезным. Для обучения же решению примера 4 достаточно сказать, что критическим путем называется самый длинный путь, ведущий от начальной точки к конечной, критической работой является любая работа, лежащая на критическом пути. Отсюда путем перебора вычисляем длины всех путей от пункта 0 к пункту 4: путь 0 — 2 — 4 составляет 55, 0 — 4 составляет 30, 0 — 1 — 4 — составляет 21 и 0 —

1 — 3 — 4 составляет 44. Таким образом, критический путь — это путь 0 — 2 — 4, его длина 55, из предложенных вариантов на нем лежит работа (2, 4). Задача решена полностью, но вряд ли такое решение имеет отношение к деятельности менеджера, и уж точно не позволяет судить о сформированности практических компетенций.

Еще больше удивляет задача на функцию полезности.

Пример 5: Дана функция полезности U = 3√x + y. Тогда кривая безразличия имеет вид…

Все, что должен сделать преподаватель, чтобы обучить решению данной задачи, это сказать, что кривая безразличия, это такая же функция, что и функция полезности, но только равная константе С. Излишне говорить о степени полезности такого задания, хотя отметим, что и сама функция полезности по мнению В. И. Лоскутова, доктора экономических наук, профессора МАЭУ, является не применимой на практике [9].

Не спасают ситуацию и появившиеся недавно кейс-задания. Согласно определению, приведенному тем же сайтом [1] кейс-задание представляет собой задание, состоящее из описания некоторой реальной, конкретно-практической ситуации и совокупности вопросов (задач) к ней. Выполнение студентом кейс-задания требует решения поставленной проблемы (ситуации) в целом и проявления от студентов умения анализировать конкретную информацию, отслеживать причинно-следственные связи, выделять ключевые проблемы, выбирать оптимальные методы решения и др. В то же время, реально представленные кейс задания, которые удалось найти на сайте сложно представить себе, как реально встречающиеся ситуации.

Пример 6. Инвестор вложил одну треть своего капитала, равного 30 тыс. рублей в акции А, а оставшуюся часть — в акции В. Через год сумма его капитала увеличилась на 4 тыс. рублей. Если бы инвестор распределил свой капитал наоборот, то увеличение капитала составило бы 3,5 тыс. рублей.

Вопрос 1: Процентный доход по акциям А составил…

Вопрос 2: Отношение доходности акций А к доходности акций В составляет…

Варианты ответа: 10/3, 3/10, 2/3, 3/2.

Вопрос 3: Пусть процентный доход по акциям В не меняется, установите соответствие между процентным доходом по акциям А и капиталом инвестора

• 1.    15 %.       2. 20 %.         3. 25 %.

Варианты ответов: 33500 руб., 34000 руб., 34500 руб., 35000 руб., 35500 руб.

Задача является типичной школьной задачей на составление системы уравнений. Треть от 30 тысяч рублей составляет 10 тысяч, остальная часть — очевидно 20 тысяч. Пусть х — процент по акциям А, у – процент по акциям В (выраженный в дробных долях), тогда доход от вложений составит 10х + 20у = 4. Если бы средства были распределены наоборот, то доход составил бы 20х + 10у = 3,5. Решая полученную систему находим, х = 0,1, а у = 3/20. Ответ 1: доход по акциям А составил 10 %. 1Ответ 2: (1/10 : 3/20 = 2/3).

Для ответа на вопрос 3 отмечаем, что вложение 20 тысяч в акции В в таком случае всегда будут приносить 20 × (3/20) = 3 тыс. рублей. Тогда вложение 10 тысяч при 15% годовых принесут дополнительно 1,5 тысячи рублей, при 20% — 2 тысячи и при 25% — 2,5 тысячи. Ответ 3: 1 — 34500 руб., 2 — 35000 руб., 3 — 35500 руб.

При решении этого задания возникает вопрос: каким образом в реальной ситуации инвестор узнал, сколько бы он получил от вложения средств наоборот, если ему была не известна даже процентная ставка по акциям, по которым он уже этот доход реально получил? Зачем ему понадобилось отношение доходов? Искусственность данной задачи состоит в том, что она вызывает у студентов ощущение ненужности получаемых знаний, знаний ради знаний, что автоматически ведет к снижению познавательного интереса, а значит и качества этих самых знаний. А ведь программный курс высшей математики как раз и позволяет сформировать у студентов и заинтересованность в математических знаниях, и соответствующие умения и навыки, необходимые в практической деятельности. Многочисленные примеры таких интересных и полезных задач можно найти в работах [3–7, 10], а в работе [11] приведен эффективный и вычислительно удобный пример решения практической задачи на нахождение оптимального плана инвестирования.

В заключение статьи хотелось бы отметить, что целью работы является не критика создателей базы тестовых заданий [1, 2]. Личные многочисленные попытки автора создать собственные тесты с «улучшенными» условиями быстро приводили к обнаружению новых недостатков, и, вероятно, большинство преподавателей согласятся с тем, что если уж «выбирать из двух зол», то предоставленные на официальном сайте тесты являются даже очень хорошими. Настоящей работой нам бы хотелось обратить внимание на принципиальное противоречие применения тестирования с компетентностным подходом. В связи с этим отмечается необходимость совершенствования образовательного процесса в рамках компетентностно-го подхода, а также форм оценивания сформирован-ности профессиональных компетенций [12, c. 77], [13, c. 42-43], [14, c.241]. К недостаткам метода тестирования также можно отнести сложность выполнения работы корректирующего характера. Для выполнения работы над ошибками требуется иметь текст условий, который не списывается во время выполнения теста, как это делается во время решения обычного задания. Преподавателю остается не ясна причина, по которой допущена ошибка (вычислительная погрешность, невнимательность, неправильное понимание условия, незнание теоретического материала или иные причины). Правильный ответ может быть получен после некоторого числа попыток, без понимания того, как он получен. Нет гарантий, что обучаемый понял метод решения задачи, которая была при тестировании выполнена успешно — не исключается вариант «случайно угадал»; при этом коррекционная работа по выполнению этого задания уже не проводится, так как задание принято как выполненное. Таким обра- зом, применение тестов как формы контроля в процессе обучения является не только трудоемкой (нужно написать не только условие задачи, но и варианты ответов), но и одновременно не эффективной процедурой, в результате чего мы получаем меньше информации о качестве усвоения материала обучаемыми, по сравнению с традиционными формами контроля.