К вопросу о соотношении фундаментализации и инноваций в вузовском курсе алгебры

To a problem on a relation fundamentalization and innovations in a high school course of algebra

In article the opportunity of introduction of innovations – changes of the maintenance and technology of teaching of a high school course of algebra due to use of system of computer mathematics Maple is considered. It will allow to strengthen fundamentalization algebraic education of students-mathematicians .

В условиях лавинообразного нарастания информации возникает проблема поиска новой формы отбора и синтеза знаний. Учитывая, что сущность образования во многом определяется фундаментальностью, целостностью и направленностью на удовлетворение интересов личности, а также то, что динамизм современного общества требует необходимости многократной переориентации выпускников вуза, необходимо усиление фундаментализации образования через внедрение инноваций. Возникающая в связи с этим проблема интенсификации обучения состоит в тесной связи с совершенствованием технологий обучения, которые опираются на на- учные результаты конкретных наук, психологические исследования и современные компьютерные технологии.

Сегодня имеются новые технические и педагогические возможности, средства, которые позволяют реализовать практически любые новые технологии и новое содержание образовательного процесса и которые дают возможность решить проблему адаптации образования к изменяющейся ситуации в науке, к новым потребностям в обществе.

В настоящее время стремительное развитие получили информационные технологии и, в частности, компьютерная математика. Разработка систем компьютерной математики с элементами символьных (аналитических) вычислений, их обычно называют системами компьютерной алгебры (СКА), стала высочайшим достижением компьютерного «интеллекта».

Широко используется ряд систем компьютерной алгебры: Reduce, Mathcad, Derive, Maple, Mathematica, MATLAB и др. Из них бесспорными лидерами являются пакеты Mathematica и Maple.

В данной статье мы рассмотрим возможности использования пакета Maple в процессе обучения алгебре в вузе. Пакет Maple воплощает новейшую технологию символьных вычислений, и, по данным сайта , в настоящее время этот пакет используют более 5 миллионов студентов, ученых, специалистов и исследователей практически каждого ведущего университета и научно-исследовательского института в мире, включая такие, как Cambridge, Stanford, Oxford и др.

Для курса вузовской алгебры характерно наличие сильной алгоритмической содержательнометодической линии. Заметим, что для большего числа задач, решаемых по определенному алгоритму, в Maple имеются соответствующие программы. Поэтому технология процесса обучения алгоритмической составляющей курса алгебры может быть, например, следующей: определение понятия, выявление и обсуждение алгоритма его применения, решение задач с привлечением Maple, а далее уделить большее внимание решению частично-поисковых и исследовательских задач из этой же темы. Тогда студенты могут сконцентрироваться на важных концепциях, а не на чаще всего громоздких алгебраических вычислениях и преобразованиях.

Давайте проанализируем, что, например, должен знать студент о понятии определитель, кроме определения, – несколько свойств и несколько способов его вычисления. Сколько вместе с тем аудиторного и внеаудиторного времени уходит на вычисление определителя? Не проще ли, вычислив определитель один или два раза вручную и усвоив алгоритмы его нахождения, вычислять в дальнейшем определитель, используя Maple? Рассмотрим, например, следующую задачу –№12.2 [2]:

Вычислить определитель:

a

b

c

d

- 1

- 3

- 2

- 4

LinearAlgebra\-Determniant^ 1);

-^b-Vc-VSdLla .

Далее, реализуя дидактические идеи Пойа о том, что главная задача обучения математике – в развитии мыслительных способностей человека, процесс изучения определителя должен состоять из задач, подобных, например, такой: "Найти наибольшее значение определителя третьего порядка, у которого два элемента равны 5, а остальные равны +1 или –1". Затем можно предложить такую задачу: нельзя ли изменить условие, рассмотреть определитель четвертого порядка и проанализировать, насколько усложнится процесс решения и изменится ответ при этом, т.е. исследовать, насколько в этой задаче существенно то, что порядок определителя равен трем?

Аналогично можно поступить с решением системы линейных уравнений, с использованием как метода Гаусса, так и правила Крамера. Ведь метод Гаусса проходит сквозной линией по всему курсу алгебры первого семестра начиная с решения системы линейных уравнений, вычисления ранга матрицы, нахождения базиса пространства, поиска фундаментальной системы решений однородной системы уравнений, и даже при нахождении жордановой нормальной формы матрицы мы используем метод Гаусса, тогда как идейно такие задачи на вычисления достаточно просты. Поэтому задачи такого вида нужно, видимо, решать с использованием систем компьютерной алгебры.

Рассмотрим следующие два примера (№35.15 и №8.2(и) из [2]), показывающие, как можно использовать Maple для нахождения базисов суммы и пересечения линейных оболочек, натянутых на данные системы векторов, и также для исследования системы линейных уравнений, со- держащих параметр.

тт „                                              „       ,         < a,, a^, а, > и < b1,b2,b3 >:

Найти базисы суммы и пересечения линейных оболочек ^{1 2 3}

а 1 = (1,2,1), а 2 = (1,1,-1),    а 3 = (1,3,3);

b = (1,2,2,), b ₂ = (2,3,-1), b 3 = (1,1,-3).

al := vector^ [1,2, 1 ]); a2 := vector^ [ 1, 1, - 1 ]); a3 — vector^ [ 1, 3, 3]); W — vector{ [ 1, 2, 2]); b2 := vector { [2, 3, - 1 ]); b3 — vector ([ 1, 1, - 3 ]);

al := [ 1 2 1

a2 := [ 1 1 - 1

a3 "  13 3

bl := 1 2 2

b2 := [ 2 3 - 1

b3 := 1 1 -3

Найдем один из базисов суммы этих подпространств:

> sumbasis { {al, a2, a3}, {bl, Ь2, Ь3{\,

.

п                                                              (3,5,1)

Базис пересечения этих подпространств состоит из одного вектора :

> intbasis { {al, а2, аЗ}, {bl, Ь2, Ь3{{;

.

Решение следующей задачи на Maple будет несколько сложнее, но, овладев этой технологией, можно использовать шаблон ее решения в дальнейшем.

Исследовать систему и найти общее решение в зависимости от параметра (1 + 2 ) x 1 + x ₂ + x ₃ = 2 ² + 2 ,

< x 1 + (1 + 2 ) x ₂ + x ₃ = 2 ³ + 2 ²,

X i + x 2 + (1 + 2 ) x 3 = 2 ⁴ + 2 ³;

Запишем основную матрицу этой системы уравнений:

1 + X    11

1     1 + X1

1      1    1 +

Далее укажем столбец свободных членов:

d — vector^ [X" + 3 X, Я³ + 3 X", X* + 3 1?])

2                    2 43

d -^— Х+ЗХХ+ЗХ X + 3 X

Решим эту систему: >

х :" [ -X2 + 2 2 X - 1 2 X2 - 1 + X3 - X ]

Если в векторе не ясно, где какие координаты, то можно попросить Maple записать вектор в

столбец.

.V •= convert (х, matrix У,

-К + 2

2 X — 1

2 X — 1 + X — X

При таком способе решения системы линейных уравнений особые случаи не выявлены. Поэтому выпишем расширенную матрицу данной системы:

>

Х+1 1    1 х2 + зх

1 Х+1 1 х3 + з х2

1      1 х + 1 X4 + з х3

Приведем эту матрицу к ступенчатому виду, причем не используя деления на выражения, содержащие параметр:

>

1 X + 1       1

СГ= О -X X

X3 + 3 X2 х4 + 2 х3 - 3 х2

о О X3 + 3 х2 -4 х3 - 3 х2 + 5 х5 + 5 х4 + х6

Необходимо теперь разложить выражения, содержащие ^, на множители: >

а =

1 X + 1      1                 х2 (3 + X)

0-х X         х2 (3 + X) (X- 1)

о о X2 (3 + X) х2 (3 + X) (2 х2 - 1 + х3 - х)

Мы видим, что особые случаи - это ^ = ⁰ и ^ = ³

.

Подставив эти значения ^ , найдем соответствующие решения исходной системы уравнений:

>

01 '=Х^Х

>

СП :=

1-2  10

0 3-3 0

0 0 0 0

Т1 := submatrix (СП, 1 ..3, 1 ..3); dl

■= convert (submatrix (СП, 1 ..3, 4 ..4), vector У,

T1 := 1 -2   1 0 3-3 0 0 0 dl := [ О О О ]

х ■= linsolve{Tl, dl,'r', t);

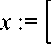
q>2 := x—>eval{x, X = 0)

ф2 :=x—>x

x = o

> CI2 := evalm{map{q>2, CI})’,

CI2 :=

0 0 0 0

0 0 0 0

T2 := submatrix {CI2, 1 ..3, 1 ..3); d2

■= convert {submatrix {CI1 , 1 ..3, 4 ..4), vector);

T2 :=

1 1 1

0 0 0

0 0 0

d2 := [ 0 0 0 ]

> x := linsolve{T2, d2,'r', t);

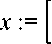
^1 4 4 4

.

Таким образом, данная система линейных уравнений имеет при ^{λ ≠ -}3, ^{λ ≠} 0 единственное

x := решение:

2 о 1 л 2            3

-X + 2 2 X - 1 2 X - 1 + X -X

При ^{λ = -} 3

x := система имеет решение:

4 ^zi h

где t 1– свободная переменная.

При ^{λ =} 0 система неопределенна и x :=    ^-?i ^— ^2 ^1 ^2

имеет

следующее

множество решений:

где t 1 и t 2 – свободные переменные.

Итак, использование пакета Maple, сокращая вычислительную составляющую курса алгебры, вернее громоздкие алгебраические вычисления и преобразования, повышает уровень изу- чения дисциплины, поскольку

• •    говоря о вычислениях, В.И. Арнольд подчеркивает, что "сила математики – не в них, и преподавание математики не должно сводиться к вычислительным рецептам" [1, c.28];

• •    за счет высвободившегося времени и усилий большее внимание уделяется концептуальным, идейно и методологически важным вопросам, что ведет к усилению фундаментализации процесса обучения алгебре;

• •    использование компьютерных технологий позволяет повысить компьютерную грамотность студента и овладеть базисными квалификациями, которые являются одним из аспектов фундаментализации образования;

• •    обращаясь к истории, можно заметить, что уменьшение вычислительной составляющей наблюдалось и в школьном курсе алгебры. Не так давно при изучении логарифма числа пред-

• Л.Х.Цыбикова, Л.В. Абашеев, И.И. Баглаев, Т.П. Батомункуева. Особенности процесса обучения в летнем профильном лагере

лагалось решить достаточно много задач вида: вычислить log ^ab для конкретных чисел а и b , для этого использовалась даже логарифмическая линейка. В настоящее время в связи с усилением функциональной линии задач такого вида практически нет в школьных учебниках, кроме, может быть, типа: найти log^ab при b ⁼ 1, b ⁼ a , или b ⁼ aⁿ .