К вопросу о структуре вакуума

Структура вакуума изучается квантовой теорией поля, которая не устает представлять ее очень сложной и, действительно, не предлагает для описания структуры вакуума ничего, согласующегося с представлениями классической физики.

Ниже предлагается такая структура, которая следует только из решения уравнений Максвелла – не делается никаких дополнительных предположений.

В разделе 2 доказано (как решение уравнений Максвелла), что может существовать т.н. волна-И-частица (ВИЧ), которая представляет собой кубический объем вакуума, а котором пульсирует стоячая объемная волна. Важно отметить, что этот объем не имеет каких-либо границ - физических или образованных неоднородностью среды. ВИЧ не излучает сквозь грани куба, но на каждой грани есть электрическая напряженность, вектор которой направлен перпендикулярно этой грани.

Величина энергии, частота и напряженность на гранях куба являются функциями только размера куба. Видимо, существует наименьший объем куба, определяемый минимумом кванта энергии.

Множество этих ВИЧ могут заполнить пространство целиком, без промежутков. И именно такая структура описывается ниже. Такая структура встречается в природе [4] – на рис. А и рис В показаны т.н квадратные волны на море. Но вначале мы рассмотрим структуру и свойства ВИЧ.

Рис. А.

Рис. В.

а, а -

• (8)

• (9)

• (10)

• (11)

• (12) волна,

• (13)

2.    Типизация волн-И-частиц

Итак, в [1] предложена модель волны-И-частицы (ВИЧ), которую мы применим здесь. Для удобства читателя приведем здесь краткое описание этой модели.

Напряженности электрического и магнитного полей, найденные как решение уравнений Максвелла, имеют вид

E_x (x, У,z, t) = e_x cos(аx)sin(ау)sin(аz) sin(at) , (1) E_y (x, у, z, t) = e_y sin(аx)cos(ау)sin(аz) sin(at) , (2) E_z (x, у, z, t) = e_z sin(аx)sin(ау)cos(аz) sin(at), (3) H_x (x, у, z, t) = h_xsin(ax)cos(ay)cos(az) cos(cot') , (4) H_y (x,у,z, t) = h_y cos(аx)sin(ау)cos(аz) cos(at) , (5) H_z (x,у, z, t) = h_z cos(аx)cos(ау)sin(аz) cos(at) , (6) где e_x ,e y ,e_z , h_x , h y , h_z - постоянные амплитуды функций, константы. Амплитуды связаны уравнениями вида h _z = 0 , ^hy     ^hx ,

,           Eto

• ^hx =    ^ ^e x,

ey = ex, ez     2ex и могут быть определены при данном ex. Круговая частота а) = c«V4.5.

Этими уравнениями описывается объемная стоячая существующая в объеме куба, ребро которого имеет длину

L = п/а.

Плотность электромагнитной энергии этой волны определяется как

W = еЕ2 + дН2, причем в этой волне выполняется условие и = е|е2 | = д|н2|.

Полная электромагнитная энергия волны в кубе

Wo = t/^L3.

Эта энергия НЕ изменяется во времени .

Плотности потоков энергии по координатам определяются по формуле

-=0=I

Рассмотрим формулу

I

E y H z E z H x E x H y

—

—

—

EzHyl E xHz\. EyH\

E y H z — E z*	^1 ^ =0                  (17а)
EyHr — E^ E x H y — E y4

(17b)

Заметим, что cos(ax)=cos (a 2) = cos (a“~) = 0.

Следовательно, напряженность, у которой в определении функций (1-6) встречается косинус некоторой координаты, на грани, перпендикулярной этой координате, принимает нулевое значение. В формуле (17а) зачеркнуты те напряженности, у которых встречается косинус соответствующей координаты. Видно, что компоненты в этой формуле равны нулю. Следовательно, на всех гранях куба выполняются условия вида

I

E y H z E z H x E x H y

—

—

—

EzHy

ExH. EyH

z

x

I=0

т.е. куб не излучает энергию .

На каждой грани куба существует магнитная напряженность, вектор которой перпендикулярен этой грани. Например, на грани, перпендикулярной оси ох, вектор (4) принимает значение

H x = sin(ax)=sin (a 2) = sin (a 2^) = 1,

- см. также (13). Итак, поток энергии не выходит из этой грани, но существует магнитная напряженность перпендикулярная этой грани. Аналогичный вывод можно сделать относительно остальных граней куба.

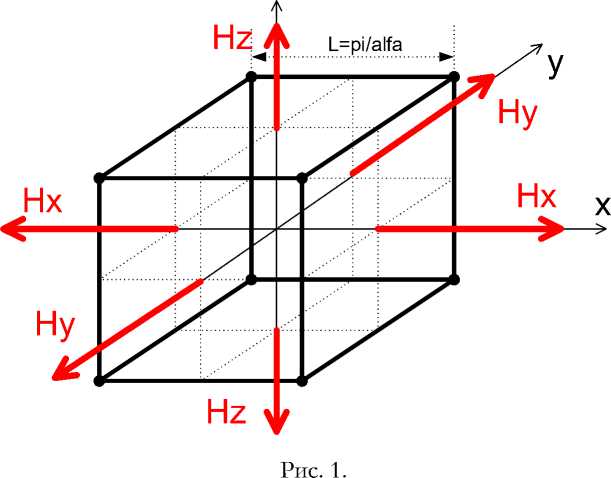
На рис. 1 показаны магнитные напряженности, выходящие из граней куба. Важно отметить, что напряженность H_z в данном случае отсутствует по условию (7), хотя и показана на рис. 1. На гранях с отрицательным значением координаты напряженности направлены в отрицательную сторону, т.к. при этом sin(ax)=-1 .

Поток энергии не выходит из грани, перпендикулярной оси ох, но циркулирует по этой грани, т.к. плотности потока S y и S_z на этой грани не равны нулю. Например, S y = E_zH x — E x H_z - см. (17).

Здесь H_z — 0, E_z Ф 0, H_x Ф 0 - см. (19). Следовательно, S_y Ф 0 . На этой грани, также, как и во всем объеме, имеется энергия с плотностью U , не изменяющаяся во времени. Следовательно, на этой грани и, вообще, на всех гранях постоянно существует давление , равное плотности энергии U .

Рассмотренный тип ВИЧ будем обозначать, как ВИЧ-1.

По аналогии с [1] можно рассмотреть другое решение уравнений Максвелла, которое отличается тем, что вместо решения вида (7-11), используется решение вида

ez — 0.                                                  (28)

6 y —  б х, е = - ^h бХ       а хх , hy — ^ х, h z — -2 h х.

(29) (30) (31) (32)

Аналогично предыдущему, здесь также на всех гранях куба выполняются условия вида (18), т.е. куб не излучает энергию. На каждой грани куба существует магнитная напряженность, вектор которой перпендикулярен этой грани. Отличие состоит в том, что напряженность Hz также присутствует, т.к. в этом случае выполняется условие (32).

По аналогии с ВИЧ-1 и ВИЧ-2 можно рассмотреть два других решения уравнений Максвелла, которые отличаются тем, что вместо напряженностей вида (1-6) рассматриваются напряженности вида вида

H_x (%, у, z, t) = h_х cos(a%)sin(aу)sin(az) sin(wt) , (41) H_y (%, у, z, t) = h у sin(a%)cos(ay)sin(az) sin(wt) , (42) H_z (%, у, z, t) = h_z sin(a%)sin(ay)cos(az) sin(wt), (43) E_x (%,у, z, t) = e_xsin(a%)cos(ay)cos(az) cos(wt) , (44) E_y (%,у, z, t) = e_y cos(a%)sin(ay)cos(az) cos(tot) , (55) E_z (%,у,z, t) = e_z cos(a%)cos(aу)sin(az) cos(wt) , (46)

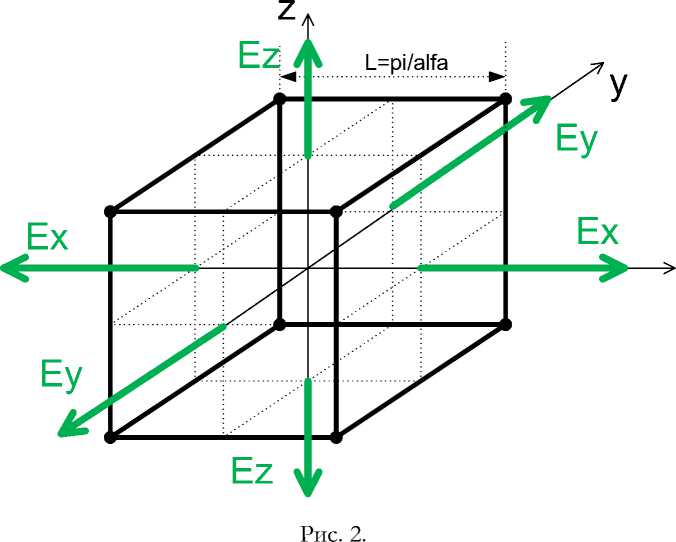
Легко заметить, что новые решения можно получить из прежних заменой обозначений E и e на обозначения H и h и наоборот. Принципиальное отличие, будет состоять в том, что вместо магнитных напряженностей, выходящих из куба перпендикулярно граням, появятся электрические напряженности – см. рис. 2.

Рис. 1 сделан в предположении, что в некоторый начальный момент времени фазы синусоидальных функций времени (1, 2, 3)

были равны нулю, а фазы косинусоидальных функций времени (4, 5, 6) и были равны максимуму. Для этого момента и показано направление векторов магнитных напряженностей на рис. 1. Будем называть такой ВИЧ как ВИЧ с фазой р = 0 . Пусть это соответствует начальному значению е_х > 0.

Рис. 2 сделан в предположении, что в некоторый начальный момент времени фазы синусоидальных функций времени (1, 2, 3) были равны максимуму, а фазы косинусоидальных функций времени (4, 5, 6) и были равны нулю. Для этого момента и показано направление векторов электрических напряженностей на рис. 2. Будем называть такой ВИЧ как ВИЧ с фазой р = тт/2 . Пусть это соответствует начальному значению h._x > 0.

Еще четыре варианта ВИЧ можно получить, принимая в качестве исходных данных отрицательные значения е_х и И_х в тот же самый момент времени. В этом случае на рисунках 1 и 2 векторы напряженностей должны быть направлены в грань (а не из грани куба)

В таблице 1 перечислены все варианты ВИЧ.

Таблица 1

ВИЧ	Формулы для Е и Н	Данные	Формулы для е и h	Рисунок	Напряженности
1	1-6	И z = 0 ех > 0 р = 0	7-11	Рис. 1	Hz = 0 Н х,у > 0
	Несимметричный ВИЧ. Векторы Н направлены из куба
2	1-6	ez = 0 hx > 0 р = тт/2	28-32	Рис. 1	Hx,y,z > 0
	Симметричный ВИЧ. Векторы Н направлены из куба
3	41-46	ez = 0 hx > 0 р = тт/2	7-11	Рис. 2	Ez = 0 Е х, у > 0
	Несимметричный ВИЧ. Векторы Е направлены из куба
4	41-46	И z = 0 ех > 0 р = 0	28-32	Рис. 2	Е х,у^ > 0
	Симметричный ВИЧ. Векторы Е направлены из куба

5	1-6	h z = 0 ех < 0 р = тт/2	7-11	Рис. 1	Hz = 0 Hx,y < 0
	Несимметричный ВИЧ. Векторы Н направлены в куб
6	1-6	ez = 0 Йх< 0 р = 0	28-32	Рис. 1	Hx,y,z < 0
	Симметричный ВИЧ. Векторы Н направлены в куб
7	41-46	ez = 0 hx < 0 р = 0	7-11	Рис. 2	Ez = 0 E x,y < 0
	Несимметричный ВИЧ. Векторы Е направлены в куб
8	41-46	h z = 0 ех < 0 р = тт/2	28-32	Рис. 2	Ex,y,z < 0
	Симметричный ВИЧ. Векторы Е направлены в куб

3.    Структура вакуума

Рассмотрим теперь множество ВИЧ. Кубическая форма ВИЧ позволяет предположить, что множество ВИЧ образуют непрерывный объем — см. рис. 3. При этом ВИЧ с фазой р = 0 и ВИЧ с р = тт/2 должны чередоваться по всем направлениям пространства.

Возможны различные комбинации ВИЧ.

Может быть пространство, заполненное ВИЧ, создающими только магнитные напряженности на гранях или только электрические напряженности на гранях.

Может быть пространство, заполненное только симметричными ВИЧ или только несимметричными ВИЧ. В последнем случае в пространстве должно возникнуть направление, в котором отсутствует какая-либо напряженность в каком-либо направлении. Такой вакуум должен так или иначе проявить анизотропные свойства.

Можно предположить, что природа использует все варианты и существуют разнородные пространства.

Таким образом, каждая ВИЧ остается автономной, но вместе они образуют непрерывный объем вакуума.

Можно предположить, что все ВИЧ имеют один и тот же объем и тогда существует единая частота вакуума. Можно также предположить, что существуют различные области пространства с различным (но общим для данной области) объемом ВИЧ. Тогда эти области должны иметь разные частоты вакуума.

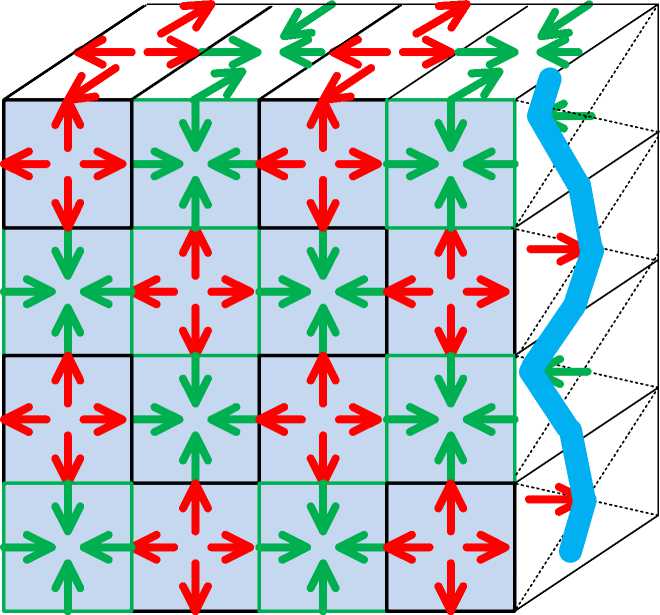
Рис. 3.

Какая-либо грань ВИЧ может оказаться на границе пустой области пространства. Тогда на границе этой области возникнет напряженность — та напряженность, которая присутствует на указанной грани ВИЧ. Такая напряженность является той данной напряженностью, которая формирует стоячую волну — см. замеч ание после формулы (11). Таким образом, напряженность на грани некоторой ВИЧ генерирует стоячую волну в пустом пространстве и тем самым создает новую ВИЧ. Таким способ ВИЧ размножаются , заполняя весь вакуум. Можно предположить, что Вселенная возникла из одной ВИЧ.

4.    Эффект Казимира

Рассмотрим правую боковую поверхность вакуумного фрагмента на рис. 3. Предположим, что эта поверхность является границей области ВИЧ. На открытых поверхностях ВИЧ в их центре показаны векторы напряженностей, входящих и выходящих их этих поверхностей. Толстая линия, огибающая концы этих векторов, условно изображает волну напряженностей на открытых поверхностях. Эти напряженности изменяются синусоидально во времени. Таким образом, на поверхности границы области ВИЧ существует стоячая волна напряженностей.

Но, главное, на открытых поверхностях ВИЧ постоянно существует давление U — см. выше. Если к этим поверхностям примыкает некоторое тело, то оно должно испытывать это давление. Таким образом, тело, находящееся в вакууме, заполненном ВИЧ, испытывает давление вакуума со всех сторон. Каждая область ВИЧ также создает давление на соседнюю область. Следовательно, ВИЧ стремится заполнить внутренние пустоты. Можно утверждать вслед за Торричели, что «вакуум не терпит пустоты».

формуле

Градиент давления в сплошном массиве ВИЧ определяется по

2U

L '

где U, L - давление на гранях куба и длина грани куба, определенные в [1]. Тогда изменение давления на некотором расстоянии А в вакууме.

^Р о = У ^А -                            (48)

Учитывая это, расположим две параллельные зеркальные поверхности на малом расстоянии друг от друга. Они сжимаются давлением бесконечного множества ВИЧ снаружи пластин и раздвигаются ничтожным давлением (2) внутренних ВИЧ. И, следовательно, давление внешних ВИЧ должно сблизить зеркала.

Читатель уже понял, что сказанное есть ничто иное, как предлагаемое объяснение эффекта Казимир - две параллельные зеркальные поверхности, расположенные на малых расстояниях в вакууме, притягиваются.

В существующей модели вакуума [2] причиной эффекта Казимира считаются “энергетические колебания физического вакуума из-за постоянного рождения и исчезновения в нём виртуальных частиц…. Происходит это вследствие того, что в пространстве между пластинами могут существовать только стоячие волны, амплитуда которых на пластинах равна нулю. В результате давление виртуальных фотонов изнутри на две поверхности оказывается меньше, чем давление на них извне, где рождение фотонов ничем не ограничено.” Кроме того, при объяснении этого эффекта признается существование отрицательной энергии. [3].

Эти ссылки приведены для того, чтобы отметить явное противоречие между предлагаемой и существующей теориями (ПТ и СТ).

В ПТ доказывается, что существует объемная стоячая волна с определенными напряженностями в узлах, а в СТ утверждается, что амплитуда напряженностей в узлах (на пластинах) равна нулю (можно доказать, что при этом не выполняется закон сохранения энергии).

В ПТ доказывается, что реальные частицы заполняют вакуум, а в СТ предполагается существование виртуальных частиц, рождение которых ничем не ограничено, а исчезновение ничем не объяснимо.

В ПТ доказывается, что существует постоянное давление вакуума на тела, а в СТ предполагается что такое давление создают волны виртуальных частицы, постоянно возникающих и исчезающих.

В СТ доказывается существование отрицательной энергии, а в ПТ сохраняется уважительное отношение к закону сохранения энергии.

Читателю предлагается выбрать, что ему больше нравится.