К вопросу о времени безотказной работы сложной системы

Известно, что под сложной системой понимают совокупность функционально связанных разнородных устройств, предназначенных для выполнения определенных функций и решения стоящих перед системой задач [1]. Одной из важных характеристик работы системы является время ее безотказной работы. Часто эту характеристику считают случайной величиной [1; 2]. Но можно рассмотреть и другой подход: определить время безотказной работы системы как случайную функцию многих переменных £(t1,..., td) = ^ (t), где d = 1,2, ..., т е. случайным полем [3]. Если использовать такую математическую модель, то для ее описания и исследования методов математического анализа оказывается недостаточно, приходится обращаться к методам функционального анализа. В частности, если предполагать, что случайное поле £(x 1, ..., xd) принадлежит пространству непрерывных функций C(K), где K = [0, 1]d – d-мерный куб со стороной единичной длины из евклидова пространства Kd, то норма этого пространства

I ^1 с = ₍m^ax) l^⁽ t i ,..., t d )

( t ₁ ,..., t_d )

не является дифференцируемой функцией ни по Фреше,

Математика, механика, информатика ни по Гато. Но чтобы оценить вероятности вида P(|^|C < r), где r e R1, требуется наличие дифференцируемости. Поэтому возникает необходимость заменить норму пространства C(K) некоторым ее приближением и, соответственно, оценить погрешность этого приближения.

Пусть X ( t ) – случайная функция банахова пространства C ( K ) с указанной выше нормой. Рассмотрим следующий функционал, определенный с помощью n -мерного интеграла:

F ( X ) =

= h In J ( e h ⁽ t) + e- hx ⁽ t) ) dt = h J ch hx ( t ) dt , ⁽¹⁾

где h > 0.

Рассмотрим, насколько хорошо приближает этот функционал норму пространства C(K). Не имея никаких дополнительных условий, на X(t) найти оценку погрешности вряд ли возможно. Одной из наиболее доступных при наблюдении характеристик случайной функции являют- ся ее приращения.

Поэтому естественным образом возникают условия на приращения функции X ( t ) . Пусть с вероятностью 1 случайная функция X ( t ) удовлетворяет условию Гельдера:

Каждый из интегралов неотрицателен, поэтому I не менее каждого слагаемого.

Пусть t ₀ – точка, где достигается значение максимума, т. е.

I ^X 0 ⁽ t )| = maxi ^{X (} t )| = X C .

7 A

Так как X ( t ) удовлетворяет условию (2), то

1 1 = J e^{h ( X (} t )^{- X (} t ^{0 ))} dt + J e-^h Mt ^- t ⁰Г dt .

^K                                I t ^- t 0 l< ⁵

Выберем «±» следующим образом: пусть

1 1 - 1 0i^a = h •

Тогда

6 = | t ^- t 0I^a .

Поэтому

1 1 = ^e

, - M

α

где ц ( Q ) - мера множества Q . В данном случае

Q = ^ t : | t - 1 0I <  h ^a

I X(t ) - X ( 5 )| <  M\t - s )|^a,              (2)

где некоторая константа M > 0,0 <  a < 1.

Расстояние в R _d определено обычным образом: d

I t ^- s i = & ⁽ t ^- s ⁾².

• V i =1

Тогда справедлива следующая оценка.

Теорема . Если X ( t ) удовлетворяет условию (2) то:

• - ^hln2 <  X _c- F ( X ) <  h^C

1 (^  d ।   z ।    ( d  1)   2     )

< — M + — In h + In Г — + 1 + — In n , h (a ( 2 )   d    J

есть шар в евклидовом пространстве R_d с центром в точке _ 1

t ₀ и радиусом h ^α .

Используя формулу объема шара в d-мерном про странстве, получаем следующее:

d z ( -1)

Ц( Q ) = —П--I h ^a I ,

Г ( d + 1) ⁽    )

z to где Г(z) = J xz-1 e-xdx - гамма-функция, n = 3,1415926 [4].

Поэтому

to где Г(z) = Jxz-1 e-xdx - гамма-функция, n = 3,1415...

Доказательство

Оценим выражение | X | _C – F ( X ) сверху и снизу. Сначала найдем оценку снизу:

Тогда

1 1 = ^e

d

M ^{π z}

Г ( d + 1) z

d

—

■ h ^a

.

I ^X\c - ^F ( ^X ) =

I

I X C ^{- F} ( X ) <  h In ^e

¹ln e^hX C - ²In [ch hX ( t ) dt = hh

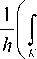
e hX ( t ) + e - hX ( t )     )

hX C      ^{dt J}

e ± hX ( t )

Так ^как -Cv <  ¹

то ^e

I X C - F ( X ) <  2 J dt = 2 ( K ) = 2,

K где ц(K) - мера множества, а K = [0,1]d. Функция y = In x является возрастающей, поэтому

|X C - F ( X ) <  h ln(2)-' =- h In 2.

d π ^z

Г ( d + 1) z

\ -1

d

—

■ h ^a

1 1 d. , . „[ d J 2       )

= — I M +— In h + In Г1 — + 1 1+ — In п I .

h

d

Теорема доказана. Обозначим

Ф ( h ) = ¹ 1 M + d In h + In ГI d + 1 |+ -ln п h (      2           ( 2 J d

Замечание 1 . Если размерность пространства R_d есть четное число, т. е. d = 2 k, k = 1, 2, ..., тогда

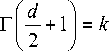
Поэтому

Найдем оценку сверху. Обозначим

I = J e^{h (} X ⁽ t ^{) -}l X C ) dt ₊ J e^{h ( -} X ⁽ t H X c ) dt .

KK

Ф ( h ) = ¹ 1 M + ^k- In h + У In l + 1ln h ( a         , =2       k

_12 k, , , , , 1, < — | M +--In h + k ■ In k — In п h (a      k

π

Если размерность пространства R_d есть нечетное число, т. е. d = 2 k + 1; k = 0, 1, 2, ..., то, используя следующее свойство гамма-функции [4]:

Самое плохое приближение возможно при

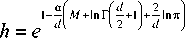
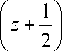
2 2 ^z -1

π

v (2 z )

получаем, что ф( h) = -h

M + ^k^ In h + (2k +1)x x ln(2k +1) - (k + 2) + | - + - | In n

.                               I k 2 )

Замечание 2 . В погрешности приближения нормы | X | с случайного поля X ( t ) параметры M , a , d являются фиксированными, исключением является параметр h . Очевидно, что чем больше h , тем лучше приближение.