К вопросу о выборе исходных данных при автоматизации тестирования программ

Тестирование программ – это процесс проверки качества программ, включающий в себя проектирование тестов [1], выполнение тестирования и анализ полученных результатов [4].

Неудачно спроектированные тестовые наборы существенным образом снижают эффективность тестирования и понижают доверие к результатам его анализа. Задача подбора тестовых наборов данных, соответствующих типу программ и охватывающих все области входных данных, поступающих на вход программы в процессе эксплуатации, представляется актуальной.

Постановка задачи

В статье рассмотрен подход к подбору тестовых наборов данных (ТНД) из всего допустимого множества исходных данных (ИД) программ [4] для организации автоматизированного тестирования расчетно-логических программ (РЛ-программ).

Под РЛ-программами будем понимать программы, позволяющие выполнять обработку больших объемов числовых данных. Аналогами такого рода программ могут быть программы аналитической обработки многомерных данных (например, OLAP-кубы, реализованные на основе универсальных реляционных СУБД).

Оговорим ограничения на характер ИД:

• •    числовые ИД образуют многомерный куб с независимыми (в статистическом смысле) измерениями в общем случае разной физической природы;

• •    в процессе функционирования программ ИД выбираются случайным образом и могут принимать любые действительные значения из некоторых промежутков ненулевой длины – диапазонов изменения ИД в каждом измерении куба;

• •    законы распределения данных в измерениях (плотности распределения) – произвольные (но известны или поддаются формализации) [5];

• •    группы ТНД должны выбираться в пределах диапазонов изменений ИД с вероятностью, соответствующей плотности распределения ИД.

Суть последних двух ограничений поясним особо. По умолчанию предполагается, что ИД имеют равномерный закон распределения. Но это идеальный вариант, и он далеко не всегда соответствует действительности. Если ИД подчиняются закону распределения, отличному от равномерного, подбор тестов должен производиться с учетом законов распределения данных по каждому измерению [3]. Таким образом, вместо формирования ТНД с фиксированным шагом «вдоль» каждого измерения более предпочтительным является формирование блоков тестовых данных, назовем их эквивалентными блоками, мощность множества каждого из которых пропорциональна вероятности появления входных наборов данных программ из диапазона, соответствующего диапазону ТНД.

Баглюк С.И., Нечай А.А. К вопросу о выборе исходных данных...    105

Выбор эквивалентных блоков ТНД

Формирование эквивалентных блоков достигается при выполнении условия равенства объемов, ограниченных гиперповерхностью, образованной плотностью распределения системы нескольких (по количеству измерений) наборов ИД. Пояснить этот тезис можно на примере одномерного куба, у которого данные «вдоль» его одного измерения (обозначим его x ) имеют, например, нормальный закон распределения с плотностью распределения f ( x ).

Качественно такая ситуация отображена на рисунке 1. Условием выбора эквивалентных блоков ТНД (блоков с одинаковым количеством данных для тестирования), взятых из диапазонов ( x _1, x ₂) и ( x ₃, x ₄), является равенство площадей («объемов» в случа _{x 2}е гипер-поверх _x н₄ости) под кривой плотности распределения f ( x ): S ₁ = S ₂. При этом S ₁ = J f ( x ) dx и ^S 2 = J ^f ( x ) ^dx ^[3]. x 1

x 3

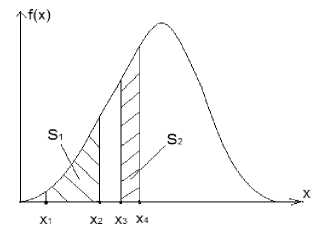
Рис. 1. Равенство площадей под кривой плотности распределения параметра x

Для общего случая n измерений необходимо рассматривать плотность распределения функции n параметров f (x1,x2,…,xn). В соответствии с первым ограничением (статистическая независимость данных между каждым измерением многомерного куба) справедливо выражение f (x1, x2, …, xN) = f (x1)∙f (x2)∙…∙f (xN ), которое выполняется при соблюдении условия нормировки:

d max

., x n ) dx 1 dx 2 ... dx n = 1,

JJ... J ^f ( x 1^{, x} 2 ,

dmin где dmin = (x1min , x2min, …, xnmin ) – минимальные значения ИД по каждому измерению; dmax = (x1max , x2max, …, xnmax) – максимальные значения ИД по каждому измерению.

Тогда требование равенства объемов, образованных под кривыми гиперповерхности, примет следующий вид:

где

x 1 j 2

V j = V k , x 2 j 2

Vj= J f ( x 1 ) dx 1 J f ( x 2 ) dx 2 • x1j1                       x2j1

x 2 k 4

x nj 2

. J f ⁽ x n ) dx n ;

x nj 1

x nk 4

V k = J ^f ( x 1 ) dx 1 J ^f ( x 2 ) dx 2 . J ^f ( x n ) ^dx n ;

x 1 k 3

x 2 k 3

x nk 3

106 в ыпуск 4/2020

нижний и верхний пределы xmj1, xmj2 и xmk3, xmk4; m = 1, 2, …; n – границы интервалов двух эквивалентных j- и k-блоков ИД по аналогии с границами площадей S1 и S2 на ри- сунке.

В качестве примера рассмотрим двумерный куб, в котором данные в измерении x1 под чинены закону распределения Коши: f (x ) =—-,------г, а данные в измерении x подчиП (1+x 2)    2

e - x 2

нены нормальному закону распределения f ( x 2 ) =f ( x 2 ) = —;=.

Соблюдаем условия нормировки:

x1max                          x 2 max

J ^f ( ^x 1 ) ^dx 1 = 1; J ^f ( ^x 2 ) ^dx 2 = 1.

x1min

Выражение для двумерной поверхности плотности распределения данных в этом кубе примет вид

x 1max x 2max ∬ x 1min x 2min

, n(1 + x2),

\

„ 2

e 1

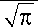
dx ₁ dx ₂.

Искомое выражение для равенства объемов при выборе эквивалентных блоков ИД примет вид

x 12 x 22 ∬ x ₁₁ x ₂₁

, n(1+x2),

/

„ 2

e 1

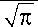
^x 14 ^x 24

dx 1 dx 2 = Я

,                   ^x 13 ^x 23

, n(1+x2),

„ 2

e 1

)

dx ₁ dx ₂.

\

Заключение

Рассмотрен подход к выбору блоков тестовых данных, названных эквивалентными блоками, соответствующих вероятности появления входных наборов данных программ из аналогичных числовых диапазонов. Рассмотренный подход позволяет:

• •    автоматически формировать ТНД для определенного тапа программ;

• •    выполнять выбор блоков тестов в соответствии с частотой поступления на вход программ тех или иных входных данных;

• •    изменять объемы тестирования (увеличивать/уменьшать) без нарушения пропорциональности относительных размеров тестовых наборов по диапазонам изменения входных данных.