К вопросу о выборе проектных параметров перспективной ракеты-носителя среднего класса

Объектом исследования является перспективная двухступенчатая ракета-носитель (РН) среднего класса.

Исследование ведётся из условия неизменности ракетного блока первой ступени РН. При проведении моделирования используются характеристики ракетного блока первой ступени перспективной РН [1].

При проведении исследования были заданы следующие требования:

• •    выводимая масса полезного груза (ПГ) — не менее 18 т;

• •    массово-энергетические характеристики ракетного блока первой ступени принять неизменными (маршевый двигатель на базе РД-171М);

• •    использование стартового комплекса «Зенит-М» [2].

Облик РН, описанной в работе [1], предполагает применение на второй ступени двигателя тягой 60,3 тс, создаваемого на базе существующего двигателя, имеющего лётную квалификацию. Это позволяет сократить сроки его создания.

Одним из очевидных путей повышения энергетических характеристик перспективной ракеты-носителя является увеличение массы топлива второй ступени. Однако, при использовании двигателя тягой 60,3 тс увеличение массы топлива привело бы к низкой тяговооружённости и, как следствие, к большим гравитационным потерям. Поэтому увеличение массы топлива при использовании этого двигателя нецелесообразно.

В данной работе выявлены максимальные энергомассовые возможности перспективной двухступенчатой РН с неизменным ракетным блоком первой ступени с двигателем РД-171М. Двигатель для ракетного блока второй ступени является новой разработкой.

постановка задачи

Цель данного исследования — найти зависимость массы ПГ от начальной массы и тяги двигателей второй ступени РН и определить оптимальные значения этих параметров, доставляющие максимум массы ПГ. Характеристики первой ступени принимаются неизменными.

математические модели и методы

Для моделирования баллистики выведения ракетой-носителем ПГ используется система дифференциальных уравнений движения (СДУД) материальной точки в стартовой системе координат [3], ось х которой направлена по азимуту пуска; ось у — вдоль линии отвеса от Земли; ось z дополняет систему координат до правой.

Потенциал земного эллипсоида соответствует нормальному гравитационному полю [4]. Модель атмосферы принята стандартной невозмущённой в соответствии с ГОСТ 4401-81 [5].

Метод интегрирования СДУД — метод Рунге–Кутты–Фельберга седьмого (восьмого) порядка точности с переменным шагом интегрирования [6].

Для всего интервала моделирования движения РН принимается, что рассогласование Δϕ отсутствует, т. е. система управления — идеальная, ϕ( t ) = ϕ_пр + Δϕ, Δϕ = 0, ϕ( t ) = ϕ_пр, где ϕ_пр — временная программа угла тангажа.

Управление первой ступенью РН задаётся посредством программы изменения угла атаки, а именно — коэффициентами экспоненциальной зависимости угла атаки от времени [3]:

а(t) = |amax| 4ea(t 1-t)(ea(t 1—t) - 1), где amax — предельное значение угла атаки; t1 — время окончания вертикального подъёма и начала программного разворота; a — коэффициент, определяющий интенсивность разворота.

Управление второй ступенью РН задаётся посредством коэффициентов линейно-временной программы тангажа

ф( t) = Фо + Ф t, где ф0 — начальный угол тангажа; ф — первая производная по углу тангажа.

При управлении либо по углу тангажа, либо по углу атаки для определения угла, не заданного явной зависимостью, следует воспользоваться равенством а = ф - 6, в котором один из операндов задаётся явной временнóй зависимостью, а 6 — угол наклона вектора скорости к местному горизонту.

Для решения краевой задачи выведения конечной массы на требуемую орбиту применяется многопараметрический метод Ньютона [7]:

J =

∂ y _{1   ...} ∂ y ₁

∂ x ∂ x

1 m

∂y     ∂y m ... m

∂ x     ∂ x

1m xk+1 = xk – Jk–1(f(xk) – yd), где J — якобиан частных производных выходных функций по входным параметрам; xk — вектор входных (управляющих) параметров на текущей итерации краевой задачи; f(xk) — вектор значений выходных (контролируемых) функций при текущем векторе управляющих параметров; yd — вектор требуемых значений выходных функций.

При решении краевой задачи необходимо задаться условием завершения: при выполнении неравенства ( f ( x _k ) – y _d ) < 8 расчёт останавливается.

Также при наличии одного свободного параметра в задаче моделирования баллистики выведения используется метод «золотого сечения» [8] для оптимизации траектории выведения по массе ПГ.

ход решения и результаты

Для решения поставленной задачи необходимо определить зависимость массы ПГ от начальной массы и тяги второй ступени РН. Необходимо провести многократное моделирование полёта РН, решить пространственную задачу баллистики выведения [3] для некоторого дискретного множества сочетаний начальной массы и тяги второй ступени РН. Также необходимо учитывать ограничения по максимальной продольной перегрузке, максимальному скоростному напору и районам падения (РП) отделившихся частей. Для сравнения вариантов принято, что ПГ выводится на круговую орбиту высотой 200 км, наклонением 51,7° с космодрома Байконур, а также учитываются заданные ограничения на параметры траектории движения.

Для обеспечения выведения на требуемую орбиту, как говорилось ранее, необходимо решить многопараметрическую краевую задачу (в зависимости от количества входных и выходных параметров). Основными управляющими параметрами являются:

• •    максимальный угол атаки |a_max| — на этапе полёта первой ступени;

• •    максимальный угол тангажа Ap_max — на этапе полёта второй ступени;

• •    скорость разворота по тангажу Ф^. — на этапе полёта второй ступени;

• •    скорость разворота по рысканию \ф — на этапе полёта второй ступени.

Чтобы обеспечить требуемые параметры орбиты, решается либо двухуровневая краевая задача:

• •    на внутреннем уровне: два входных параметра — коэффициенты линейно-временной программы тангажа второй ступени РН, и два выходных параметра — высота перигея и высота апогея;

• •    на внешнем уровне: один входной параметр — максимальный угол атаки первой ступени, и один выходной параметр — дальность РП первой ступени, либо решается задача оптимизации, в которой максимальный угол атаки первой ступени — параметр оптимизации для достижения максимальной массы ПГ.

  
  
  

Рассматривая задачу выбора проектных параметров второй ступени ракеты-носителя как оптимизационную, необходимо задаться переменными оптимизации:

• •    Δ m ^II — добавочная масса второй ступени;

• •    Δ P ^II — добавочная тяга второй ступени.

Под словом «добавочная» подразумевается значение переменной, прибавляемое к номинальному значению соответствующей характеристики второй ступени. Номинальные значения энергомассовых характеристик второй ступени составляют: P ^II = 60,3 тс; m ^II = 71,5 т; m _К^II = 6,5 т — тяга, начальная и конечная массы номинального варианта блока второй ступени, соответственно.

Для всех вариантов второй ступени удельный импульс принят равным 3 541 м/с (361 с).

В состав ракеты космического назначения (РКН) входит головной обтекатель (ГО) массой 1 900 кг, ∅ 4,35 м. Головной обтекатель сбрасывается в РП первой ступени РН с соблюдением ограничения на максимальный скоростной напор при сбросе. При проведении дальнейших исследований целесообразно, учитывая, что размеры РП створок ГО превосходят размеры РП ракетного блока первой ступени, рассмотреть для ГО существующий РП больших размеров на дальности более 1 400 км при некотором снижении массы выводимого ПГ.

Масса переходного отсека, соединяющего полезный груз, головной обтекатель и вторую ступень, входит в конечную массу второй ступени.

Номинальная масса ПГ при Δ m ^II = 0, Δ P ^II = 0 составляет 18,0 т.

Также следует задать область поиска и шаг по каждой из переменных (рис. 1). Принимаем, что диапазон поиска по переменной Δ m ^II ∈ [0; 100] т, по Δ P ^II ∈ [0; 150] тc, а шаг по обеим переменным равен 5 т (тс). Дальнейшее увеличение стартовой массы второй ступени РН нецелесообразно, так как оно приведёт к значительному снижению начальной тяговооружённости всей РН.

Таким образом, результатом решения станут поверхности, образованные наборами точек с координатами ([выходной параметр]; Δ m ^II; Δ P ^II).

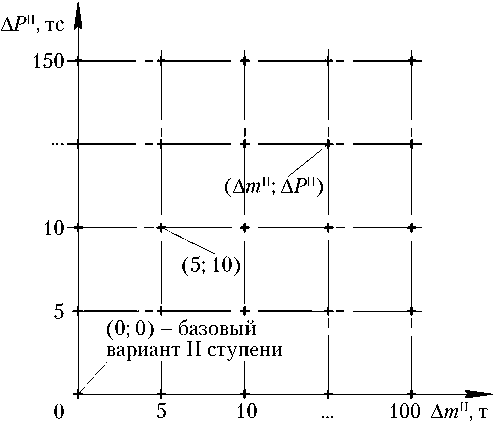
Рис. 1. Дискретное множество сочетаний добавочной массы и добавочной тяги второй ступени

Данное исследование проводится в два этапа.

• 1    этап: определяется картина изолиний или поверхность масс ПГ в зависимости от массы топлива и тяги второй ступени. Данный этап решается многократным моделированием выведения РН с различными сочетаниями масс топлива и тяги второй ступени. Картина изолиний требуется для наглядного понимания поведения и зависимости выводимой РН массы от сочетаний проектных параметров второй ступени. Решение происходит без учёта РП первой ступени.

• 2    этап: поверх задачи моделирования траектории выведения решается задача математической оптимизации методом последовательного квадратичного программирования [9]. Этот алгоритм основан на методе множителей Лагранжа и условиях Каруша– Куна–Таккера. Решение оптимизационной задачи даёт точное сочетание массы топлива и тяги второй ступени при поиске максимума ПГ.

В ходе первого этапа при моделировании выведения РН для каждого варианта второй ступени рассчитываются следующие выходные параметры: H _кр, m _кон, L _I, где H _кр — высота круговой орбиты (отсчитывается от среднего радиуса Земли 6 371,11 км); m _кон — конечная масса второй ступени (включает массу ПГ) на требуемой орбите; L _I — дальность центра РП отделившейся первой ступени РН. С использованием вышеуказанных параметров определяются зависимости m _кон(Δ m ^II; Δ P ^II) и L _I (Δ m ^II; Δ P ^II).

При моделировании выведения РН со всеми вариантами второй ступени из области поиска получен график линий уровня конечных масс, приведённый на рис. 2.

наличии задела по двигателю, обеспечивающему попадание в эту область, но не обладающему строго оптимальной тягой, наиболее целесообразно создавать двигатель на имеющемся заделе.

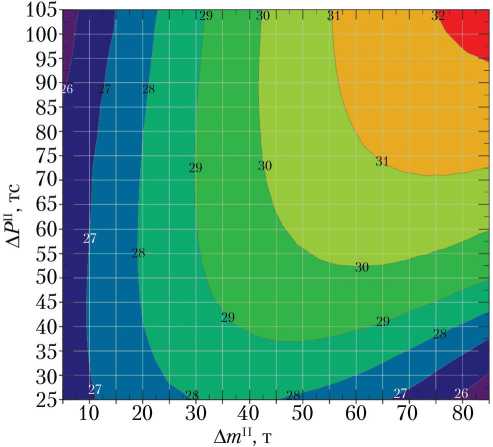
Рис. 2. График линий уровня конечных масс mкон(ΔmII; ΔPII), т

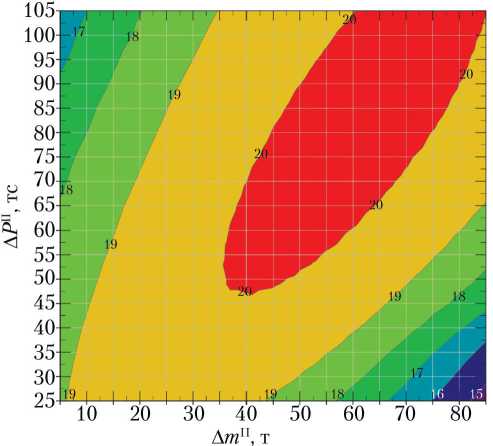
Рис. 3. График линий уровня масс полезного груза mПГ(ΔmII; ΔPII), т

По этому графику линий уровня очевиден рост выводимой конечной массы с увеличением массы и тяги второй ступени, но неочевидно поведение массы полезного груза.

Для определения аналогичной зависимости для массы ПГ m _ПГ(Δ m ^II; Δ P ^II) необходимо для каждого варианта РН из конечной массы РКН на низкой околоземной орбите вычесть конечную массу второй ступени. По авторской оценке отечественной ракетно-космической техники при определении массы ПГ принято, что на каждую 1 т добавочной массы второй ступени приходится 40 кг массы конструкции, а на каждую 1 тс добавочной тяги — 20 кг массы конструкции двигателя.

Также в результате расчёта РН с каждым вариантом второй ступени можно рассчитать массу рабочего запаса топлива второй ступени, вычитая из начальной массы второй ступени конечную массу второй ступени и массу ПГ.

В результате пересчёта получился график линий уровня массы ПГ, показанный на рис. 3.

Рассматривая график линий уровня масс ПГ, можно сделать вывод, что область значений Δ m ^II и Δ P ^II, в которой масса ПГ достигает значения более 20 т, довольно велика. Поэтому при

В результате второго этапа исследования с помощью методов математической оптимизации найден максимум массы ПГ — 20,2 т при значениях Δ m ^II = 64,10 т и Δ P ^II = 83,55 тс. Стартовая масса РКН составляет 595 т. В связи с увеличением стартовой массы РКН может потребоваться модернизация пускового стола, а именно — увеличение его несущей способности.

Массив значений m _ПГ(Δ m ^II; Δ P ^II) получен в ходе первого этапа (без ограничения на требуемые дальности РП отделившейся первой ступени РН). Для каждого варианта также получено значение дальности падения отделившейся первой ступени.

Для наглядности наложим графики линий уровня m _ПГ(Δ m ^II; Δ P ^II) и L _I(Δ m ^II; Δ P ^II) друг на друга (рис. 4) и определим варианты РН, которые обеспечат попадание первой ступени в РП с заданной дальностью.

По полученному графику можно достаточно наглядно и просто определить, какой вариант РН удовлетворяет требованию по дальности РП.

В область значений Δ m ^II и Δ P ^II, в которой масса ПГ достигает значения более 20 т, попадает один из существующих РП с дальностью 663 км. Произведём более мелкое разбиение на диапазонах

Δ m ^II ∈ [55; 65] т, Δ P ^II ∈ [70; 90] тc: шаги примем 1 т и 2 тс, соответственно. В трёхпараметрической краевой задаче зададим третий параметр L _I = L _I* = 663±δ км и смоделируем выведение ПГ с вариантами второй ступени, лежащими в вышеуказанной области значений, и дополнительным ограничением на дальность РП (рис. 5).

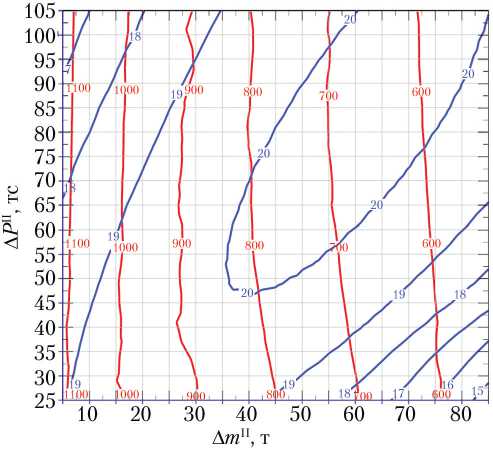
Рис. 4. График линий уровня масс полезного груза и дальности РП первой ступени ( — — дальность РП;

^— — масса ПГ)

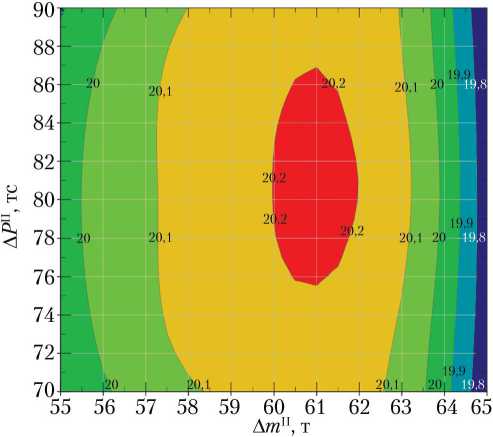
Рис. 5. График масс полезного груза при решении трёхпараметрической краевой задачи (LI = 663 км)

Анализируя данный график при наличии третьего контролируемого параметра, отметим, что экстремум массы ПГ становится более «острым»: при относительно небольшом изменении значений оптимизационных параметров масса ПГ резко уменьшается по сравнению с аналогичной поверхностью первого этапа. Для рассмотренного РП масса ПГ соответствует массе ПГ без учёта РП (см. рис. 3). Это обусловлено тем, что для оптимального сочетания массы и тяги координаты точки падения первой ступени без прицеливания в конкретный район оказались очень близки к одному из существующих РП.

При условии уменьшения статической нагрузки на агрегаты стартового стола найдём такое сочетание добавочных масс и тяги второй ступени, при которых стартовая масса РКН будет минимальной, и будет обеспечиваться попадание первой ступени в существующий РП на расстоянии 882 км. С помощью графика, приведённого на рис. 4, получено сочетание Δ m ^II = 30 т; Δ P ^II = 40 тс; масса ПГ — 19,8 т, а стартовая масса РКН составляет 565 т.

выводы

В процессе поиска оптимального сочетания тяги и массы второй ступени найден максимум массы ПГ: при увеличении начальной массы на 64 т (135 т — полная начальная масса) и тяги на 84 тс (144 тс — полная тяга) масса выводимого ПГ равна 20,2 т. Обеспечивается попадание отделившейся первой ступени в существующий РП с дальностью 663 км.

Также рассмотрен вариант РКН с меньшей стартовой массой для уменьшения нагрузки на стартовый комплекс: при увеличении начальной массы на 30 т (101 т — полная начальная масса) и тяги на 40 тс (100 тс — полная тяга) масса выводимого ПГ равна 19,8 т. Обеспечивается попадание отделившейся первой ступени в существующий РП с дальностью 882 км.

Исследование показало, что при использовании задела по первой ступени с двигателем РД-171М и стартового комплекса «Зенит-М» может быть создана РН среднего класса грузоподъёмностью до ≈20 т на низкой околоземной орбите высотой 200 км. При этом выполняются типовые ограничения на параметры траектории движения и используются существующие районы падения отделившихся частей. Условиями создания такой РН является разработка маршевого двигателя второй ступени тягой

100…140 тс. Может потребоваться модернизация пускового стола в части увеличения его несущей способности.