К вопросу о выборе структуры математической модели отопительного прибора

При вычислении необходимой площади поверхности теплообмена отопительных приборов, а также и при разработке математического обеспечения автоматизированных систем управления отоплением зданий необходима математическая модель, описывающая зависимость мощности (тепловой производительности) отопительного прибора от его входных величин. В настоящее время предлагаются к использованию несколько таких моделей [1–2], в частности, широко используется следующая модель:

w = kF [ t вх + t обр - 1 ) ,                      (1)

1              2в

ного теплоносителя – воды. Тогда, используя известные соотношения, например, для прямоточной схемы движения теплоносителей, получим:

W₂ = lim( C i ( t вх C 2 — —^

-

t в )

1 - e

- (—+—) kF

C 1 C 2

1 + C 1

)=

C 2

- kF

= C 1 ( t вх - 1 в )(1 - e ^C 1 ),

где W ₂ – мощность прибора (тепловой поток),

вычисленная по второму варианту модели.

Заметим, что совершенно такой же результат

где W1 – мощность прибора (тепловой поток), вычисленная по первому варианту модели, k – коэффициент теплопередачи, F – площадь поверхности теплообмена, tвх и tобр – температура теп- лоносителя соответственно на входе и выходе из прибора, tв – температура внутреннего воздуха помещения. Если при этом учесть, что, W1 = C1 (tвх -1 в), где С1 - полная теплоемкость массового расхода теплоносителя (в данном случае первичного), данную модель можно переписать в следующем виде:

kF

^W 1 =---- kF " ⁽ t вх ^- t обр ),                        ⁽²⁾

1 +----

2 С ₁

Структура второго варианта математической модели может быть определена, если учесть, что отопительный прибор – это, вообще-то, теплообменный аппарат, у которого полная теплоемкость массового расхода воздуха C2 (в данном случае вторичного теплоносителя) во много раз больше полной теплоемкости массового расхода первич- получается, если рассмотреть противоточную схему.

Запишем отношение мощностей, вычисляе- мых по первой и второй моделям:

W 2

W 1

- kF

(1 ⁺ 1^) - ’¹ - ec¹)

kF

C 1

Таким образом, получаем соотношение мощ- kF ностей как функцию аргумента :

C 1

Wl₌ / kF 1 .

W 1     I C 1 J

В свою очередь выражение

kF можно оце-

C 1

нить следующим образом:

, , , I tвх + tобр    ,  I        Л      „    \ kF I 2       tв J = C1 (tвх   tобр ) ,

Панферов В.И., Милов А.Е.

К вопросу о выборе структуры математической модели отопительного прибора

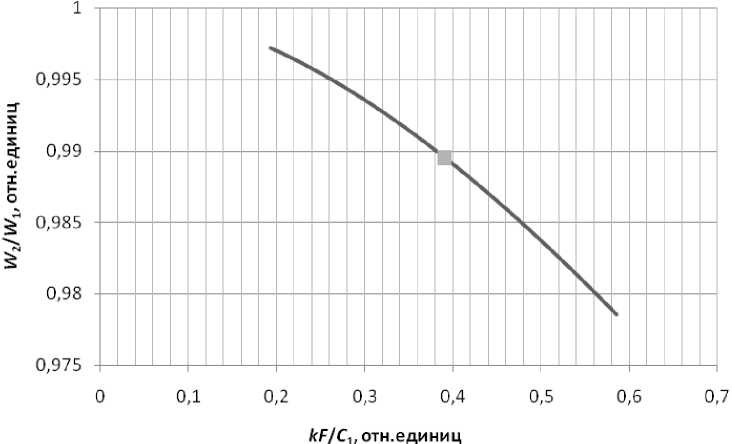
W   kF

График зависимости — = f (---)

W ₁      C ₁

Различие значений мощности по рассмотренным моделям для помещений с разной расчетной температурой воздуха

tпом, °С 16 17 18 19 20 21 22 23 kF C1 0,376 0,382 0,388 0,394 0,4 0,407 0,413 0,42 W2 W1 0,9902 0,9899 0,9896 0,9894 0,989 0,9887 0,9884 0,988 kF =   t вх t обр

C   t вх + t обр t в

Для стандартных расчетных условий принято, что t _вх = 95 ° С, t _обр = 70 ° С, t в = 18 ° С, следова-

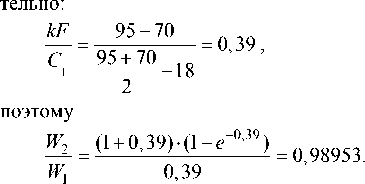
Таким образом, при расчетных условиях разность в значении мощности отопительного прибора, вычисленной по указанным моделям, не превышает 2 %. Оценили также отношение мощностей в наиболее вероятном диапазоне изменения kF     kF    kF аргумента : [0,5 ∙      ; 1,5 ∙      ].

C ₁           C ₁          C ₁

W

График зависимости отношения ²

kF от

C

;

в данном диапазоне представлен на рисунке.

Из рисунка видно, что в данном диапазоне различие значений мощности не превышает 3 %.

Как известно, расчетная температура внутреннего воздуха может быть различной для различных типов отапливаемых помещений. В связи с этим рассмотрели помещения с различной температурой t _в при режиме работы системы отопления по графику «95/70 °С». Результаты представлены в таблице.

Как видно из таблицы, различие вычисленных мощностей тем меньше, чем меньше температура отапливаемого помещения.

Выводы

Показано, что вычисляемые по двум вариантам модели тепловых потоков отопительных приборов различаются в реальных режимах работы не более чем на 3 %, поэтому обе рассмотренные структуры модели следует считать практически равноценными. В связи с тем, что структура первой модели заметно проще для математических преобразований, то она и рекомендуется для использования как при проведении стандартных теплотехнических расчетов отопительных приборов, так и в составе алгоритмического обеспечения систем управления процессом теплоснабжения.

Краткие сообщения