К вопросу о вычислении амплитуды рассеяния на радиально-симметричных упругих включениях в идеальной жидкости

В терминах амплитуд рассеяния включений решается широкий круг задач, в том числе и задачи расчета радиационного давления в различных первичных полях [1–3]. Библиография, посвященная тематике рассеяния на различных включениях, обширна (см., например, обзор в работе [4]).

Наиболее популярным видом неоднородностей в задачах вычисления радиационного давления являются однородные жидкие и упругие шарообразные включения. Несмотря на это, в большом количестве работ, посвященных, например, упругому однородному шарообразному включению, отсутствует подробное решение и единообразие в представлении конечных результатов, часто они количественно отличаются, что приводит к неопределенности. Анализу этих публикаций на предмет степени их совпадения будет посвящена другая работа, а в настоящей работе сначала предполагается подробный разбор решения задачи рассеяния на упругом однородном шарике, а затем с помощью примененного в этом разборе аппарата — решение такой задачи также в кусочнослоистом радиально-симметричном и непрерывно радиально-неоднородном шариках.

ОДНОРОДНЫЙ УПРУГИЙ ШАРИК

Линейное уравнение движения в векторной форме для идеально упругого однородного изотропного тела при отсутствии объемных сил имеет вид [5–7]

ц A u + ( Л + ц ) VV • u - р u = 0.            (1)

Если вектор перемещений u представить в виде суммы продольной ul (потенциальное поле) и сдвиговой ut (соленоидальное поле) составляющих u=u i+u t;

ul = VФ ;  ut = V x T ; VT = 0, то уравнение (1) распадается на два волновых уравнения — скалярное и векторное:

1                            1 -

АФ--ф = 0;   A T--T = 0.

c ₁ ²                         c ₂ ²

Для гармонических колебаний u = U e - ^imt волновые уравнения (2) сводятся к скалярному и векторному уравнениям Гельмгольца соответственно:

АФ + к 12 Ф = 0; A T + k 22 T = 0. (3)

В (3) под Ф и T уже понимаются амплитуды соответствующих колебаний.

Выше приняты обозначения:

Л + 2 ц c \ = \            ,

ρ

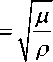
скорости, а k1 , k2 — волновые числа продольных и поперечных волн соответственно; Л, ц — постоянные Ламе; Ф и T — соответственно скалярный и векторный потенциалы векторного поля u (U). Векторное поле T допускает разложение на три векторных поля [7, т. 2]:

Т = L + M + N .              (4)

В этом представлении L — продольная часть вектора Т : L = V v 0 , которая не имеет физического смысла и при вычислении вектора U _t дает нуль. Два оставшихся вектора M и N в сферических координатах допускают разложение [6–9]

M = rot( r v 2 ), N = rotrot ( r v 1 ) .            (5)

А если учесть только составляющие этих векторов, ротор которых отличен от нуля, то

M = rot( r v 2 ), N = r v 1 .            (5а)

Здесь r — вектор в сферической системе координат: r = r ₀ r , где r ₀ — единичный орт; r = |r|. Для потенциалов Ф и v , , i = 1,2 справедливо уравнение Гельмгольца в сферической системе координат

1 V r 2 «И! r ² д r V д r V v, )_v

1 д

+ r2 sin 0 д0

д (Ф sinθ д0 Vv,

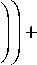
k 1 1

V ^k 2 )

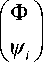
= 0,

а общее решение (8) преобразуется к виду

(Ф A

I = Z " Idn(k 12r)Pn(cos0).(8а)

Vv,) n"0VBn)

'

r ² д r V

r ² — Ф | +

д r д2

1 д f_a д a --I sin 0 — Ф | + r ² sin 0 д 0 V      д 0  )

+ r2 sin2 0 дф2

Ф + к 1² Ф = 0,

-⁽ r ² д r V

? д 1        1 д ( . д 1

r2 —v, | +--I Sin 0---У, | + дr   )  r2 sin 0 д0V     д0   )

д ²

+ r2 sin2 0 дф2 i = 1,2.

У , ^{+ k} 2 ^ , = ⁰,

Здесь P_n (cos θ ) — полиномы Лежандра.

Таким образом, в стационарном случае вектор смещения точек упругого тела в сферических координатах выражается через три скалярные функции следующим образом:

U = U l + U t = grad Ф + rot( M + N ), (10) где M и N выражаются из (5а) через скалярные функции ψ ₁ и ψ ₂ , удовлетворяющие уравнению (7). Скалярный потенциал Ф удовлетворяет уравнению (6). С учетом (5) окончательно можно записать [6, 9]:

U = grad Ф + rotrot( r v ₂) + rot( r v 1 ). (11)

Пусть составляющие вектора смещения в сферической системе координат равны U = (U r , U_θ , U_ϕ ) . Для дальнейших рассуждений необходимо выписать компоненту U_ϕ вектора смещения через скалярные потенциалы [6, 9]:

Частные однозначные решения последних уравнений Гельмгольца имеют вид

I ( r , 0 , Ф ) = d n ( k , r ) P nm (cos 0 ) е^,тф ; i = 1,2;

V v )

n = 0,1,2,...; m = - n ,..., n ,

^и Ф =

r sin 0 д ф

д

— Ф +

1 д ( д --1 r—v ₂

r sin 0 д r V д ф

д д0^‘   (12)

где d_n ( k_ir ) — одна из сферических функций Бесселя j_n ( k_ir ) , Неймана n_n ( k_ir ) или Ханкеля h_n ^{(1) (2)} ( k_i r ) ; P_n^m (cos θ ) — присоединенная функция Лежандра.

Общее решение уравнений (6), (7) определяется так:

Для случая осевой симметрии, когда отсутствует компонента смещения и_ф = 0 (тело не подвергается кручению), очевидно, что Ф = Ф ( r , 0 ), v ₁₂ = v ₁₂( r,0 ), и из (12) видно, что либо v 1 = 0, либо v 1 = v 1 ( r ). В последнем случае v 1 ( r ) удовлетворяет уравнению (см. уравнение (9))

1 д ( 2 д 1 , 2

——I r ² — v i I ^{+ k} 2² v i = ⁰, r ² д r V   д r   )

Г ф

V v

to n

=zz n=0 m=-n

A

_RI d n ( k , r ) P n ^m (cos 0 ) е^тф .        (8)

V B nm )

В случае осевой симметрии, когда функции Ф и y i , i = 1,2, не зависят от угла азимута, в (6), (7) д ² исчезает член, содержащий оператор :

д ф²

e ±,k2 r решением которого являются функции (ухо-r дящие и приходящие сферические волны). Последние решения не годятся, т. к. они неограниче-ны при r = 0. Остается решение v1 = 0 . Решение (11) с учетом этого перепишется в виде

U = grad Ф + rotrot( r ^ 2 ), (13)

В случае, когда упругий шарик находится в идеальной жидкости, граничные условия на поверхности упругого шара таковы [10, 11]:

– радиальная компонента смещения в жидкости uir + usr и в упругом теле Ur на поверхности шара равны uir + иД = Ul ; (14) ir sr lr = a r lr = a

– суммарное давление падающей p_i и рассеянной p_s волн в жидкости равны с обратным знаком нормальному напряжению σ_r на поверхности шара

P. + P s\_r = a = — ^O r ; ⁽¹⁵⁾

– касательная компонента напряжения на поверхности рассеивателя в невязкой жидкости равна нулю (величина σ_rϕ тождественно равна нулю вследствие осевой симметрии задачи)

O.. = 0. (16)

Выпишем нужные величины, выраженные через соответствующие отличные от нуля потенциалы. Поскольку выражения для σ_r не совпали в работах [6, с. 41] и [9, с. 111], то автором были самостоятельно выведены все нужные величины. Для этого использовалось выражение (13) для вектора смещения, а также следующие выражения для определения нужных напряжений. Согласно [12, с. 367], имеем

O = ( ^— + 2 ц ) S r + ^— ( S_e + 8_ф ) , O r e = ² MS e ,

O r = 2ц

д ² I

— bk ² +-- Ф +

¹ д r ² J

L _{2   12} д   _ д ²       д ³ 1

+ L ² + k ² r --+ 3--+ r---^₂ ,

I ^{2      2} д r     д r ²      д r ³ ) ² ,

^O r e = ² Ц

1 AfU r д e I д r

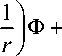
д f д ²     1 д     1    1, 2 1

+11 k-> \W-) д e |д r ² r д r r ² 2    )

где

д             1 f д

Sr =   Ur, Se = I    U e + Ur дr         r\se

S = ¹ ( Ue ctg ^{e + U} r ) , r

,

что показало полное совпадение с результатами работы [6, с. 41]. Здесь b = — = —0— ; о — 2ц (1 — 2о)

коэффициент Пуассона материала шарика, который выражается через скорости продольных и сдвиговых волн следующим образом [13]:

о =

c ₁ ² — 2 c ₂ ²

² ( c 12 ^— c 22 ) .

Запишем известные выражения для падающего и рассеянного шариком полей в жидкой среде с плотностью ρ и скоростью звука c . Так, выражение для плоской волны единичной амплитуды и нулевой фазы, распространяющейся вдоль положительного направления оси Oz , при временнóм факторе e ^— ^ t* имеет вид [7]

p_i = e flkkz = e^ikr cos ^e = j^ (2 1 + 1)( _kr ) p (cos e ). (20) 1 = 0

Выражение для поля рассеянной волны при падении волны (20) на рассеиватель с центром в начале координат имеет вид [14, 15]

1 f д 1 f д Se = ^_ —U +^_ - U

2U r ^e r U e ^r

—

U e II ;

ε — соответствующие компоненты тензора деформаций.

Окончательно нужные величины имеют вид:

to

P s = £ T 1 (2 1 + 1) ih i ¹ ( kr ) P, (cos e ) = 1 = 0

= -^( e ^{2 iS} i — 1)(2 1 + 1) Vy ¹ ( kr ) p (cos e ).       (21)

2 1 :0'                           ^{1         1X}

Здесь ( e ^{2 i5 1} — 1) = 2y = a₁ ; a₁ , 3₁ , T — некоторые коэффициенты, зависящие от волнового параметра x = ka ; a — радиус сферы; k = o / c .

В дальнейшем будем искать коэффициенты T .

Скалярный и векторный потенциалы представим формулами

u_r =— ф д r

1^a r sin e se

д I sin ^e д ё^ 2 1 ,

to

Ф = z A (2 1 + 1) i¹ j 1 ( k 1 r ) p (cos e ),              (22)

= 0 to

_V 2 = Z B 1 (2 1 + 1) ij, ( k 2 r ) P (cos e ),            (23)

= 0

вид которых обусловлен осевой симметрией и ко-

нечностью потенциалов в начале координат.

Выражение для амплитуды рассеяния получается из (21) подстановкой асимптотики функции

Ханкеля h1 ’(z) □ —i~1 -1 eiz при z ^да и вычленени-z ем множителя e . Имеем окончательно [16]: r ”

f (9, x ) = - У I, ( x )(2 1 + 1) P (cos9 ) = ik i = o

^:^У У^а1 ^{( x )(2 1 +} 1) Pi ^{(cos 9} ) =

2 ikZ 0

= — У ( e ² i⁵' ^{( x} ) - 1)(2 1 + 1) P (cos 9 ).     (24)

2 ik l : 0

Отметим, что в случае наличия множителя p ₀ в падающей волне, все остальные характеристики поля в силу линейности задачи также приобретут этот постоянный мультипликативный коэффициент.

Выпишем условия на границе (14)–(16) для парциальных коэффициентов разложений (20)– (23). Условие (14) в парциальном виде с учетом выражения (17) и дифференциального уравнения Лежандра

• 1    д ( .      d _z Л            ,

  --sin 9—P (cos 9 ) + 1 ( 1 + 1) P (cos 9 ) = 0

sin 9 д 9 1      9 9         )

можно переписать в виде

Al 4- ^j 1 ^{( k} 1 ^r ) д r

+1BJ (1 +1) j (k2 r) r r :a r : a

1 5

= ~- (Th ( kr ) + j ( kr )) pro ² д r

Здесь справа стоит парциальное радиальное смещение жидкости. Или окончательно из равенства смещений имеем

Ax j, '( X 1 ) + B, KI + 1) j ( x 2 )--^'( x ) :

ρω ²

Y

: —Ji '( x ).                              (25)

ρω ²

Здесь и далее x i = k i a , i = 1,2. Для условия равенства на границе нормальных напряжений (15) имеем

2 ρ ₁ c ₂

I    A 1 ^k 1

-          j ( x 1 ) + j "( x 1 ) '

I ^{(1 -} 2^ )               )

^{+ B}1^k 2² ( ^j 1 ⁽ x 2 ) ^{+ x} 2 ^j 1 '⁽ x 2 ) ^{+ 3 j} 1 "⁽ x 2 ) ⁺ x 2 ^j 1 "'^{( x} 2 ) ) ⁺

+ Th /( x ) :- j ( x ).                             (26)

При обработке условия (16) учтем в касательном напряжении σ_rθ (19) следующее равенство [17]:

• - -d^ P (cos 9 ) : P ’(cos 9 ).

Тогда, учитывая последнее равенство и ортогональность системы функций P 1(cos9), 1 = 1,2,... на интервале [0, п] с весом sin9, имеем для парциальных коэффициентов равенство r2

1 д 1

- A11          I j(k1r) + r \д r r)

_n ( д²    1 д

+ B ₁ 1----+--

I д r ²    r д r

^- ^ ^{+ 1 k} 22 I j ^{( k} 2 ^r ) r ²    2     )

: 0.

r : a

Или окончательно:

2 ( x 1 j '⁽ x 1 ) ^- j ⁽ x 1 ) ) A +

⁺ ( x 22 j "⁽ x 2 ) ^{+ ( 1} 2 + ^{1 - 2)} j ⁽ x 2 ) ) ^Bl = ^0.         (27)

В последнем случае для приведения выражения к укороченному виду использовалось уравнение для сферических функций r2 — + 2r- + (k22r2 -1( 1 +1)) д r2     д r j i(k2r) = 0.

Таким образом, получена система трех уравнений (25)–(27) для определения бесконечной цепочки из трех неизвестных ( A , B ₁ , I ) , 1 = 0,1,2,...

Выпишем ее в матричном виде:

г

x ₁ j_l '( x ₁)

г

2 ρ ₁ c ₂ ² k ₁ ²

—

к

_n ^ . h ( ^x i ) + ji "^{( x} i ) (1 ^— 2 ^ )

² ( x i j '( x i ) ^— j ⁽ x i ) )

1 (1 + 1) j ( x 2 )

² P c 2² k ■' ( j ^{( x} 2 ) + ^x 2 j 1 '^{( x} 2 ) + ³ j 1 "( ^x 2 ) + ^x 2 j "( ^x 2 ) ) ( ^x 2^{2 j} 1 "^{( x} 2 ) ^{+ ( 1 2 + 1 — 2) j} 1 ^{( x} 2 ) )

Y

---hi"(x ) ρω ²

h ¹ ( x )

к

Г A)

B

T

к

( X —j. '( x ) P® ²

=    ^— j i ^{( x} )

к

.

к          7

В результате решения этой системы коэффициент T определяется так:

T = _— F i j i ^{( x} ) ^{+ xj} i '( ^x )

¹     F i h i ^{1( x} ) ^{+ xh} i ”( ^x ),

и коэффициенты при производных уже с точностью до констант можно трактовать как импедансы, помноженные на парциальные колебательные скорости.

– Штрих в верхнем индексе функций означает дифференцирование по параметру x .

где

F = [ j i '( x i ) X 1 ( — 2 j ( X i ) j ( x 2 ) 1 ( 1 + 1) +

^{+ j} 1 '⁽ x i ) x i ^{( j} 1 ⁽ x 2 ^{)(2 + i + 1 2} ) ^{— j} 1 "( x 2 ) x 2² )) P® ² ]^X

^Xi ² c 2² P i ( ^{— k} i² ( ² j ⁽ x i ) j ⁽ x 2 ) ^{1 ( 1 + i) +}

^{+ j} I '⁽ x i ) x i ^{( — j} I ⁽ x 2 ^{)(2 + 1 + 1 2} ) ^{+ j} I "⁽ x 2 ) x 2² ) ) ^X

^Xl ^j I ⁽ x i )

—

—— + Ji "( x ) | + i + 2 ^    ^{1 i} )

^{+ 2} ( ^{— j} I ⁽ x i ) ^{+ j} I '⁽ x i ) x i ) ^j I '⁽ x i ) x i k 2² l ^j I ⁽ x 2 ) ⁺

^{+ 3 j} I "( ^x 2 ) ⁺ ( ^j I '^{( x} 2 ) ^{+ j} I '"( ^x 2 ) ^x 2 ) x                                X —i

— j ( x 2 ) k i² 1 (i + 1 ) X

x[ j, .( x, ) + j^

к — i + 2o

.

Замечания.

– Выражение (29) можно переписать в виде j1(x)+ xjI'(x)

T (x) =--F--------, ht i (x) + — xhji'(x)

F

СЛОИСТО-НЕОДНОРОДНЫЙ РАДИАЛЬНОСИММЕТРИЧНЫЙ УПРУГИЙ ШАРИК

Речь идет о физической модели шарика, состоящего из плотно соприкасающихся друг с другом однородных упругих сферических оболочек различной толщины с различными упругими свойствами общим числом n . В центре общего шарика может находиться либо упругий, либо газообразный или жидкий шарик и имеет номер m = i. Радиус первого шарика a ₁ , радиус общего шарика a , толщина m -й оболочки H_m . Все упругие постоянные в каждом слое также имеют соответствующий номер. Эта задача является близкой рассмотренной выше, за исключением ряда нюансов, которые необходимо отметить.

На границе между упругими оболочками должны выполняться следующие краевые условия [11, 18]:

– разница нормальных и тангенциальных смещений вдоль орта θ (смещение вдоль орта ϕ равно нулю вследствие осевой симметрии задачи) на разных сторонах всех границ, а также разница нормальных напряжений и напряжений вида rθ равны нулю, а именно

[ ^ Г ] m = ⁰, [ ^ , ] m = ⁰ , [ ^ „ ] m = ⁰, [ ^СТг 9 ] m = ⁰, m = ⁱ, n ^{— i};

– на границе общего шарика и идеальной окружающей жидкости выполняются условия (14)– (16). Аналогичные условия выполняются также и в случае, если в центре шарика находится идеальная жидкость.

Падающая волна по-прежнему определяется выражением (20), а рассеянная волна — выражением (21). Учитывая сохраняющуюся осевую симметрию задачи, можно утверждать, что скалярные Ф _m и векторные у _{2 m} потенциалы (потенциалы ψ _{1 m} в силу осевой симметрии равны нулю у _{1 m} = 0) определяются выражениями типа (22), (23), но только в слоях, за исключением первого, имеют несколько видоизмененный вид: то

Фm = ^[(2l + 1)ll ( Amj (k1 тГ) + l=0

+ A 2 mi n ( k 1 т Г )) P l (cos А ) ] ,             (32)

то

У 2 m =Z[(21 + 1) il (B1 miJi ( k2 тГ) + l=0

_ + B 2 mi n i ( k 2 т Г )) P l (<** А ) ] ,            ⁽³³⁾

m = 2, n .

В центральном шарике вследствие ограниченности поля для этих потенциалов сохраняются представления (22), (23). Далее с помощью соответствующих выражений для смещений и напряжений необходимо с помощью уравнений "сшить" все условия на границах, как это делалось в первой части статьи. Так как в слоях, кроме первого, число неопределенных коэффициентов удвоилось, задача решается введением условий на границах [ U _a L = 0 . Выпишем выражение для составляющей смещения U_θ в слое с постоянными упругими свойствами [6]:

1 д       1 д f   д    )

U _a =--Ф +--1 r—У 2 I .

r д А    r д r V д А    )

Все остальные действия представляют собой рутинный повтор с учетом многослойности проделанных в первой части статьи действий.

РАДИАЛЬНО-НЕОДНОРОДНЫЙ УПРУГИЙ ШАРИК

Возможна ситуация, когда модули упругости и плотность материала включения являются кусочно-непрерывными функциями координат. Тогда упругие колебания включения описываются в рамках теории упругости неоднородных тел.

Уравнения теории упругости неоднородных тел рассмотрены в общем плане, например, в работах

[19, 20], а применительно к радиальнонеоднородной среде — в работе [21]. Согласно [19], обобщенный закон Гука, выражающий зависимость между тензорами напряжения и деформации, для неоднородных тел выполняется так же, как и для однородных тел; причем соотношения между напряжениями и деформациями будут отличаться от соответствующих соотношений для однородных тел лишь тем, что входящие в них модули упругости являются функциями координат. Кроме того, принимается предположение, что в областях непрерывности модулей упругости и плотности материала являются непрерывными и их первые две производные по координатам. Сохраняются также формулы Коши для однородного случая, связывающие тензор деформации с производными компонент вектора перемещений. Кроме того, сохраняется также зависимость между компонентами вектора перемещений и тензором напряжений такая же, как и в однородном случае.

Волновые процессы в неоднородной изотропной упругой среде с коэффициентами Ламе λ , µ и плотностью ρ описываются векторным уравнением [20]:

(Л + 2 ц)grad divu - цrot rotu + divu grad/ + д2и

+ grad ц x rot u + 2grad ц • grad u = p ---.

д t^T

Здесь под   grad u    понимается тензор

( grad u ) =^ди- .

^,l' д x j среды (модули

А для радиально-неоднородной упругости и плотность являются функциями одной переменной: Л = Л(r), ц = ц(r),

p ₁ = p ₁ ( r )) уравнение (34) преобразуется к виду

( Л + 2 ц )grad S - ц rotrot u + Л'S r ₀ +

, „       . . „ д u.       д² п

+ ц ( г, ^x rot u + 2—) = p— .

д r       д t

Здесь штрих означает дифференцирование по r ; S = div u .

Обычно решение (35) пытаются, как и в однородном случае, искать, разделяя исходное векторное уравнение теории упругости (35) на независимые скалярные уравнения для обобщенных скалярных потенциалов. В работе [21] решение ищется в виде

U = U ₁ + U ₂ + U ₃,                  (36)

где

U i = "TT^gra^ ^{fф ф )}, f ₁( r )

U 2 = -77-r^{otrot( r} r o f >M             ⁽³⁷⁾

f ₂( r )

U 3 = rot( r r_: 0 j.

В работе [22] векторы (37) ищутся несколько иначе:

U i = V i ( r )grad( Ф 1 ( r ,9 )),

U = V 2 ( r )rotrot( r o Ф 2 ( r ,9 )),            ⁽³⁸⁾

U 3 = rotC^C r^,9 )).

Здесь U ₁ , U ₂ , U ₃ соответствуют векторам смещения продольных ( U ₁ ) и сдвиговых волн ( U ₂ , U ₃ ); f ₁ , f ₂ , ψ ₁ , ψ ₂ — скалярные функции от r ; ф , Ф i , i = 1,2,3 — некие скалярные потенциалы.

Как показано в [22], представления (37) и (11), (13) для однородного случая являются частными случаями представления (38). Однако для получения независимых скалярных уравнений для потенциалов ф_i, Ф i , i = 1,2,3 в неоднородном случае в отличие от однородного, где они изначально являются независимыми, необходимо чтобы поведение функций v i ( r ), i = 1,2, 1 = 1 ( r ), ц = ц(r ), Р 1 = р 1 ( r ) удовлетворяло некоторым дополнительным условиям. В [22, 23] показаны примеры случаев, когда такое разделение возможно. Приведем один из них:

Р 1 = Р 10

г r

r

У ro 7

Ц = Ц о —

У r0)

1 = Ц(Y - 2),

Y ( r ) = С ^ , c 2² ( r ),

V i =

r

у r o )

( r r , V 2 = 1, V 1 = —

У ro)

.

Здесь r ₀ — некоторое фиксированное значение координаты r ; ρ ₀ , µ ₀ — значения соответствующих величин при r = r ₀.

Отметим, что рассмотренный здесь способ решения задачи упругости сведением ее к независимым скалярным уравнениям для обобщенных потенциалов в радиально-неоднородном случае является достаточно трудоемким и пригодным лишь для избранных распределений параметров 1 = 1 ( r ), ц = ц ( r ), p 1 = p 1 ( r ). Уместнее, по всей вероятности, применять либо общие методы скалярного и векторного потенциалов, также трудоемкие, либо аппроксимировать задачу кусочнослоистой моделью, описанной выше.

ВЫВОДЫ

В статье последовательно рассмотрена задача расчета поля рассеяния на однородном, радиально-слоистом и непрерывно радиальнонеоднородном упругом шарике. В каждом случае векторное уравнение упругих колебаний решалось с помощью сведения последнего к независимым скалярным уравнениям для обобщенных скалярных потенциалов. В силу малой практической пригодности такого подхода в случае непрерывной радиальной неоднородности шарика предложено использовать ее аппроксимацию радиальной кусочно-постоянной неоднородностью, что позволит достаточно просто решать задачу для произвольной радиальной неоднородности упругих параметров шарика.

Для вычислений в работе использовался пакет Ma-thematica-8 (лицензия L3259-7547).