К вопросу о вычислении амплитуды рассеяния объемных и поверхностных рассеивателей

Одной из важнейших характеристик использующихся в задачах рассеяния волн и частиц является амплитуда рассеяния (ар). Ар является как бы "паспортом" рассеивателя, характеризующим его свойства. С помощью этой характеристики решаются всевозможные прямые и обратные задачи теории и практики рассеяния. В частности, знание ар отдельных рассеивателей является необходимым условием для проведения вычислений по приведенному в работе [1] и других работах автора методу учета многократного рассеяния в акустике и электродинамике. В настоящей работе некоторые подходы к вычислению ар, применяемые в различных областях теории рассеяния, адаптируются к нуждам теории рассеяния в акустике. Рассматриваются как объемные, так и поверхностные рассеиватели.

A p ( x ) + k n ( х ) p ( х )--—V p ( x ) • V p ( x ) = 0,

P ( x )                       (2)

xе R3, где x = (x, y, z); к = to I c — волновое число; n(x) = c21 c2(x) — показатель преломления, равный единице в области R3 \ D . Заметим, что в (2) предполагается дифференцируемость плотности p. После замены u = p I p получаем:

Au + K 2 (x) u = 0,(3)

где

K ²( x ) = к ² n ( x ) + — A p - - - V p .

2 p

Перепишем (3) с учетом (1) и (4) в виде неоднородного уравнения Гельмгольца:

АМПЛИТУДА РАССЕЯНИЯ ОБЪЕМНЫХ РАССЕИВАТЕЛЕЙ.

ОБЩИЕ ВЫРАЖЕНИЯ

Рассмотрим случай объемного рассеивателя, вызванного наличием в однородном пространстве R ³ некоторой ограниченной области D , включающей в себя начало координат, с возмущенными плотностью среды p 1 ( x ) и скоростью звука q( x ), x е D :

Au + к2 и =

3 1 1

31      1

= к ²(1 - n ( x )) +-- Vp --A p u . (5)

^л "       2 p

4 ( p

c(x) =

c = const, x е R ³ \ D ;

C i ( x ),      x е D ;

P ( x ) =

p = const, x е R ³ \ D ;

Решение (5) при условии наличия первичной падающей волны u i ищется формально из интегрального уравнения (ИУ) Липпмана—Швингера, которое при стандартном допущении о том, что u_i представляет собой плоскую волну u i = e ^k i ^x , где k i — соответствующий ей волновой вектор, имеет вид [3] u ( x ) = e ^{k 1 x} - к ^exp i^ tx—yt m ( y ) u ( y )d³ y ,

D 4 л |x ^- y|                     (6)

P i ( x ),     x е D ,

x е R ³, где с учетом (5)

где c и p — невозмущенные значения скорости звука и плотности среды пространства R ³.

Запишем уравнение для звукового давления p ( x ) в этом случае [2]:

1 ( 3 1 „      1

m ⁽ y ) = ^{1 -} n + -_? -—^p^-—^Ap . к ² 4 p 2 p

3 1

4 p

2 p

G ( x , у ) =----р—р--фундаментальное ре-

4п |x - у| шение уравнения Гельмгольца.

Отметим, что p ( x ) = u ( x ) в области x е R ³ \ D . Наконец, полагая p ( x) = р = const, x е R ³, приходим к обычной форме уравнения Липпмана— Швингера [3] для m ( x ):

С С                               X

^{m ( x )} = 1 ^- n ^{( x )} = 1--—-.              (7a)

c i ^{( x )}

В работе [3, теорема 8.7] показано, что уравнение Липпмана—Швингера (6) при всяком к >  0 имеет единственное решение, непрерывно зависящее от амплитуды падающей волны u_t .

Из (6) следует выражение для ар [3], получаемое предельным переходом |x| ^ ” под знаком интеграла и выделением множителя при сфериче- e ik x ской волне -:—:- :

x

k

T ^{( k} , , ^k s ) = ^-— Jexp ^{( -} г k s y ) m ( y ) u ⁽ y )d³ y .     ⁽⁸⁾

^{4 n} d

Здесь учтено, что функция u ( x ) из (6) и (8) зависит от направления падения плоской волны u ( x ) = u ( x , k, ). Из (8) очевидно, что нахождение ар в общем случае является нетривиальной задачей, т. к. для этого предварительно необходимо решить интегральное уравнение (6) и вычислить функцию u ( x , k. ) для всех необходимых значений вектора ^k..

Выражение для ар также можно получить, воспользовавшись разложением сферической волны в (6) по плоским волнам [2] и техникой, изложенной в работах [4, 5]. В этом случае выражение (6) перепишется в виде u (x) = ui + us =

= _гm x + / у =x^p( i k n x ) t     k s )d k d _k ,   (9)

2n R2    as m, n = 1,2.

Здесь k1 = (kx, ky ,a), k2 = (kx, ky, -a), a = = Vк2 - kx2 - ky2 , а Tn (ki, ks) определяется из (8). При m = 1 плоская падающая волна распространяется снизу вверх в сторону увеличения координаты z, при m = 2 — в сторону уменьшения координаты z. При n = 1 рассеянная волна распространяется снизу вверх в сторону увеличения координаты z, при n = 2 — рассеянная волна рас- пространяется сверху вниз в сторону уменьшения координаты z .

Приближение Борна для ар имеет вид [3, 6]:

T n ( k , k s ) = T n ( k m - k П ) =

= - — J exp( i ( k m - k П ) y ) m ( y )d³ y .     (10)

^{4 n} R

Как видно из (10), ар в приближении Борна зависит только от одной переменной р = k m - k П , равной вектору, соединяющему две точки на сфере радиусом k .

Следуя идее, изложенной в работе [6, с. 76], k ²

умножим обе части в (9) на--exp(-iklx)m(x), 4n l = 1,2 и проинтегрируем по x в области D. В результате получаем уравнения, связывающие ар (8) и ар в приближении Борна (10):

T m ( k„ k ) = T m ( k„ k ) +

+ _ i _ j T X,k) T n   k s )d k sx d k y ;    (11)

2n R2   as l, m, n = 1,2.

Для получения интегрального уравнения необходимо в (11) потребовать выполнения условия n = l . В результате получаем интегральное уравнение

T m ( k , k ) = T m ( k i , k ) +

+ ^j T /f k s .k ) T m ( k k s )d k x d k sy ;    (12)

2 n =2    a

Rs l, m = 1,2.

Отметим, что ИУ в виде (12) отличаются от полученных в [6] и других работах тем, что в (12) рассматривается не в 3-, а в 2-мерном импульсном пространстве.

Теперь, предварительно вычислив ар в приближении Борна (10), можно из (12) вычислить искомую амплитуду рассеяния. В работе [6] приведен пример решения ИУ (12) для потенциала Юкава.

Как видно из (12), ар T m ( k i , k ) представляет собой разрешающее ядро (резольвенту) ядра 0

T m ( k i , k ), совпадающего с ар в приближении Борна, что может быть использовано для изучения свойств ар T m ^l ( k i , k ).

Таким образом, задача нахождения ар в общем случае может быть сведена либо к решению инте- грального уравнения (6) для u (x), x е D с последующим вычислением ар из выражения (8), либо напрямую из интегрального уравнения (12).

РЕШЕНИЕ ИСХОДНОГО ИНТЕГРАЛЬНОГО УРАВНЕНИЯ (6)

Приведем некоторые методы решения исходного интегрального уравнения (6) с учетом того, что достаточно найти решение u ( x ) только в области D . После этого можно воспользоваться выражением (8) для вычисления ар, с помощью которой можно затем найти поле рассеяния [ 1 ] (такой подход является альтернативным методу нахождения поля рассеяния путем решения интегрального уравнения (8) в области R ³ \ D (см. библиографию в [3 ] )). Отметим, что ядро интегрального уравнения (6) имеет слабую особенность, поэтому его необходимо заменять близким по норме непрерывным ядром.

Аппроксимация ядра интегрального уравнения близким по норме ядром

Ядро K ( x , у ) ИУ (6) является ядром со слабой особенностью, оставаясь при этом фредгольмов-ским [ 7, 8 ] :

= I I K ^{( x} , у ) ^{- L ( x} , у ) + ^{L ( x} , у ) ^- L N ^{( x} , у )| L ^-

^-l I R I L+| R L = ^a ,                           (16)

где II R L N IL =1 L ^{- l}n IL , ^и при ^{малом е} I N L пра ^к тически не превосходит нормы ядра R L N = L - L N . После определения нормы | R 11|_м можно воспользоваться различными оценками [ 7, 9, 10 ] для получения нормы разности решений интегрального уравнения соответственно с исходным ядром и аппроксимирующим ядром. Из всего многообразия оценок приведем наиболее простую [ 11, с. 359 ] , которая применительно к ядру (13) имеет вид

|u ^{( x )} - uN ⁽ x )|_{x e D} = ^{O (a} )•                ⁽¹⁷⁾

Здесь u ( x ) — решение инт. уравнения (6); u_N ( x ) — решение инт. уравнения вида (6), где вместо ядра K фигурирует L_N . Отметим, что в указанных работах приведены более точные оценки невязки решения инт. уравнения при аппроксимации исходного ядра. Впрочем, в рамках настоящей работы ограничимся оценкой (17).

Далее рассмотрим некоторые методы решения интегрального уравнения (6).

K ( x У ) =

exp ⁽ ik x ^- у )

-тт—Л m ⁽ У )•

4 п x - у

В работе [ 8, с. 299 ] показано, что при замене ядра со слабой особенностью (13) непрерывным ядром

exp( ik |x - у |) 4 п |x - у exp( ik |x - у |) 4 пе

m (уХ m (у).

| x - у| >  ^е ;

I x - у| <  ^е -

Метод последовательных приближений

Одним из часто применяющихся является метод последовательных приближений. Пусть B — шар минимального радиуса а с центром в начале координат, описывающий включающую в себя все неоднородности область D . Тогда (6) для x , у е D может быть переписано в виде (в силу того, что m ( у ) = 0 в области B \ D )

где е — некоторая малая константа, норма разностного ядра R ( x , у ) = K ( x , у ) - L ( x , у ) равна

II ^R < ^v у )| L = max J R < ^v y ^)d y - Mv ,    ⁽¹⁵⁾

D                 2

где M = | m ( x )| |^ = max | m ( x )|, что при е ^ 0 и при достаточно малых величинах M дает хорошее приближение.

Пусть далее ядро L из каких-либо соображений в свою очередь необходимо аппроксимировать другим (к примеру, вырожденным) ядром L N ( x , у ). Тогда норма результирующего разностного ядра удовлетворяет неравенству

II R d L=| K ^{( x} , у ) - ^ln ^{( x} , у )| L =

u ^{( x )} = u i - k ²j ^eXp( ik lx ^у ) m ⁽у ) u ⁽у^)d 3 y ,

B 4 n |x - у|                     ⁽¹⁸⁾

x е D .

Как показано в [3], метод последовательных приближений сходится к точному решению при условии ka <\ V .                  (19)

M

В этом случае справедлива оценка [9]

|| u ( x ) - ur ^(x)| l

- ⁽ Ma³ k ²/²⁾ r ⁺¹.

1 - Ma ² k ²/2

Здесь

rn ur(x) = t(-1) k2nKn[uiKx),           (21)

n =0

где

Kⁿ [ u , ]( x ) =

= J ’ J-J ^{G (} X , t 1 ) m ft) ^G ft, t 2 ) m ⁽ t 2 ) -

B L B B

- G ( t n - i

У) m (t n-1)d t1d t2-d tn-1 -X 4-------------v-------------Z n-1

x m ⁽ y ⁾ u i ⁽ y ^)d y .

В случае если условие (19) не выполнено, то для k > —J— резольвенту интегрального опе-aM ратора (18) R (x, y, k2 + Я) можно вычислить с по мощью аналитического продолжения [10]

R ( x , У , к 02 + Я ) =

= R (x, У, к02) + ^R 2(x, у, ко2) + Я2 R з(х, у, к02) +..., где Rn — повторные ядра резольвентного ядра R ; k0 — некоторое значение k , для которого выполняется условие (19).

Ниже на рис. 1 приведена зависимость величи-2

ны от значения c для случая, когда в (7а) M ¹

c 1 ( x ) = c 1 = const. При этом c = 1500м/с. В точке с 1 = 1500 на графике сингулярность. Очевидно, что в окрестностях этой точки ka из (18) может варьироваться в широких пределах: от ka = 2

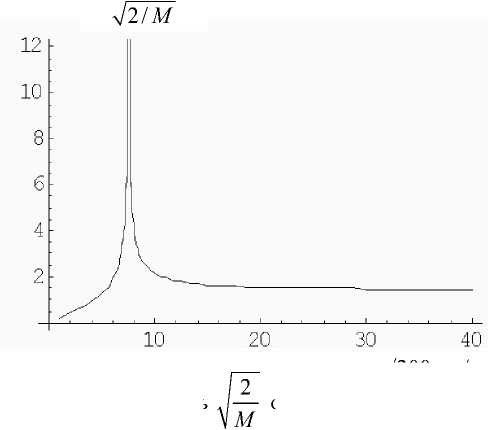
c 1 / 200, м/с

Рис. 1. Зависимость от скорости звука в неоднородном включении при c1 G [1225,2122] до ka ^~ при с1 ^ 1500±0.

Вне этой окрестности ka <  2 .

Редукция исходного трехмерного интегрального уравнения к системе одномерных

В задачах с радиальной симметрией, когда m ( x ) = m ( r ), возможна редукция трехмерного ИУ (6) к системе одномерных [12, 13 и др.]. В этом случае в ИУ (6) используется разложение [ 3, с. 29 ]

exp( ik |x - у| ) _ ik

га

4 п |x - у|

= Т" S (2 ” + 1) f n ( r , r X(c ^{os 0} ), (22) 4 n n = 0

f n ^{( r} , ^{r )} = ’

где jn (kr)hn(1)(kr), r < r, j n(kr )h n(1)( kr X r > r;

r = |x| ; r' = |y|; 0 — угол между x и у ; P _n — полиномы Лежандра; j _n ,h _n ⁽¹⁾— сферические функции Бесселя соответственно первого и третьего рода. В реальных вычислениях необходимо в (22) оперировать конечной суммой. В качестве аппроксимирующего ядра L_N возьмем конечную сумму

LN (x, У ) = ik 'N

=    m(r)X(2 n +1)fn(r, r)Pn(cos 0).(23)

4n

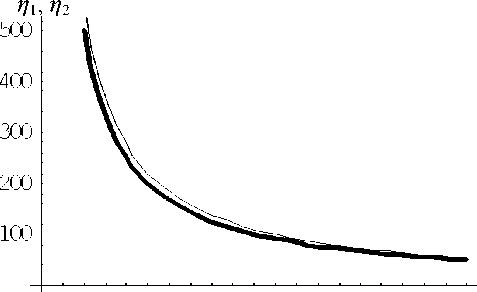
В качестве L примем ядро (14). Для оценки N необходимо вычислить норму разностного ядра ||L - L N 11. Анализ выражения (22) показывает, что модуль остаточного члена ряда как функции y при r = |x| = const и при R = |x - y| = const возрастает с ростом r . При r = 0 ряд (22) вырождается в единственный член ряда с индексом n = 0, и тем самым L ₀ ( x , y ) точно описывает ряд (22) (остаточный член тождественно равен нулю). На рис. 2 приведены зависимости 50 x | L ₁₀| и L ₅₀₀| в центре сферической волны |x - у| = 0 от величины r удаления этого центра от начала координат. Из рисунка видно, что, во-первых, точность падает с ростом r , а во-вторых, достаточно точно выполняется зависимость N ₂ x L N 1 ( r , r )| = N 1 x L N 2 ( r , r )|, N_i ^ 0.

На рис. 3–5 представлены зависимости модуля разностного ядра R_LN в зависимости от N и r 1 , где r = |y|, а точка у лежит на луче, соединяющем начало координат и точку x .

2        4       6       8       10

r , м

Рис. 2. Зависимости п 1 = 50 х| L ₁₀ ( г , г ) (-------)

и П 2 = L 500 ( r , Г ')| ⁽---------) от г

Рис. 3. Зависимости п = R, (■

3        L ₉

и П 4 = R L 100 ⁽------- ) пРи ^Г = ¹

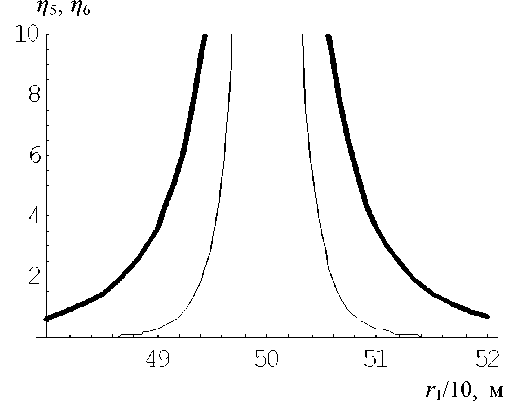
Рис. 4. Зависимость п 5 = R l 50 (-------)

и п 6 = R 180 ⁽------- ) при ^г = ⁵

Рис. 5. Зависимость п = R, (■ 7        L ₉₅

и П 8 = R L 310 ⁽------- ) пРи ^Г = ⁹

51       5| r1/10, м )

91        92

r 1 /10, м )

На рис. 3–5 утолщенные и обычные кривые соответственно рассчитаны с одинаковой точностью. Видно, что по мере роста г = |х| ( г соответственно равно 1, 5 и 9) число членов суммы N в (23) монотонно растет для утолщенных и обычных кривых соответственно в пропорции 9 : 50 : 95 и 100 : 180 : 310. Очевидно, что при достаточно больших N разностное ядро существенно отлично от нуля только в ближайшей окрестности центра сферической волны г = г и чем дальше этот центр от начала координат, тем большим должно быть N для обеспечения заданной точности.

Во всех приведенных выше расчетах было принято к = 1. Отметим, что оценку нормы остаточного члена (15), (16) достаточно уметь вычислять для к = 1. Действительно, норма разностного ядра (15) не зависит от k , а для нормы (16) легко показать, что имеет место следующее равенство:

J|^ ( к , x , y )d у = -1 2 J R L _W ( к = 1, X , Y )d Y .

B ^k kB

Здесь X = kx; Y = ky ; B = кВ — шар радиусом, в k раз превышающим радиус шара B . От- метим, что величина е, фигурирующая в непрерывном ядре (14), при переходе к координатам (к = 1, X, Y) трансформируется в величину е = ke, а шар Be ^ Вке .

После определения величины N можно записать ИУ с аппроксимирующим ядром L N :

рого рода; j_n ( kr ), п, ( kr ) — линейно независимые решения однородного уравнения (28).

Тогда решение (26) выражается через решения

(27) в виде:

где

u N ^{( Х )} = e ^x - ^k 2 J L N ⁽ x , У u N ⁽ y ^)d У ,      ⁽²⁴⁾

B

1 то

u ^{( r )} = У X ^Z n A n ⁽² n ⁺ 1) X n ^{( r} ) ^P n ^{(cos 0 )} kr n : 0                                    (29)

r e R ³,

^L N ⁽ x , У ) =

где

A n =----- а -------¹

.

ik       -N                 .

= — m ⁽ r ) £ ⁽ 2 n + 1) f n ⁽ r , r ) P n ⁽ cos 0 ).

4 n       n = 0

В рассматриваемом случае область D представляет собой шар B радиусом а с центром в начале координат (радиус а может быть и бесконечным) и m ( x ) = m ( r ). Положим в силу сим-

¹ + ^zk J m ⁽ r ) j n ^{( kr} ') X n ^{( r} ' ^{)d r} '

Асимптотика поля (29) имеет вид [ 17 ]

1 ТО                                                   т/1/ГТ u (r) = — V zn (2n + 1)e,5n sin(kr--+ 5n) Pn (cos 0), krn=0

метрии задачи, что плоская первичная волна распространяется вдоль положительного направления оси z . Тогда (6) преобразуется к виду

u ^{( r )} = e^k k - k ² J exp y r— у- m ⁽ r ') u ( r '^)d 3 r -,

B 4 n |r - r '|                        ⁽²⁶⁾

r e R ³.

Как показано в [6, 13], решение интегрального уравнения (26) сводится к решению счетной системы одномерных интегральных уравнений вида

a

X n ^{( r} ) = j, ^{( kr} ) + ^{k 2} J g n ^{( r} , ^r)m ^{( r} ) X n ^{( r} ' ^)d r ';

n = 0,1,2,...; r e [0, - ).

Здесь g n ( r , r ') =

ция Грина задачи;

1 - „ ~      ,

- ^j_n ^{( kr} ) n n ^{( kr} ). r <  Г, ^k

- j_n ⁽ kr ) n n ⁽ kr ), r >  r

I k

функ-

откуда следует выражение для амплитуды рассеяния [4, 17]

f ( 0 ) =     X (2 n + 1)( e^{l 5} n - 1)P n (cos 0 ). (30)

2 ik n = 0

Здесь 5 _n определяется выражением

a tg(5n) = -kJm(r) jn (kr)Xn(r)dr ■         (31)

Таким образом, после решения счетной системы (27) и нахождения из последних выражений постоянных S _n может быть рассчитана амплитуда рассеяния из (30). Очевидно, что замена ряда (30) конечной суммой первых N + 1 членов эквивалентна решению интегрального уравнения (24) с усеченным аппроксимирующим ядром (25).

Еще больше упрощается задача расчета ар в случае радиально-симметричной неоднородности, сосредоточенной в ограниченном шаре B .

I ^{d 2}     72

—7 + k +

( drг n = 0,1,2,...;

n ( n + 1)

g n ( r , r ') = 5 ( r - r '),

j n ( kr ) = J     J 1 ( kr ) = kr j n ( kr );

V 2    ^{n +} ₂

n n ^{( kr} ) = ^{( - 1) n +1}, Hr- J     1 ^{( kr} ) = ^kr n n ^{( kr} );

V 2    ^- ( n + ^)

J — цилиндрическая функции Бесселя первого рода; n _n ( kr ) — сферические функции Бесселя вто

СЛУЧАЙ РАДИАЛЬНО-СИММЕТРИЧНОЙ ОГРАНИЧЕННОЙ НЕОДНОРОДНОСТИ

Пусть задан сферически симметричный ограниченный рассеиватель, заключенный в шаре B радиусом а с центром в начале координат. Решение задачи рассеяния u = u_z + u s внутри области B , где u_z = e^ikz — первичная падающая плоская волна, u_s — рассеянная волна, имеет применительно к акустике вид [13]:

1 то u (r, 0) = - X i (21 +1) X1 (k, r) Pz (cos 0), (32) kr l=0

где

X" + [k2 (1 - m (r)) - l(l + 1) ]Xi = 0, r2

Xi (0) = 0, r e [0, a ]

или с учетом (7а):

- _r,₂ c ²       l ( l + 1).

X i ^{+ [ k} ~^7X- ^-^X l = ⁰ , c ₁ ²( x )       r ²

X i (0) = 0, r e [0, a ].

Вне шара B решение задачи рассеяния вид

1 то

u = -Г ^ (21 +

x j(kr) + 2ah^(kr) Pl (cos0),

имеет

где hi, ^{( 1 )}( kr ) = kr h _l ^{( 1 )}( kr ) ; h _l ^{( 1 )}( kr ) — сферическая функция Ханкеля; a _l — неизвестные постоянные. При всех a _l = 0 выражение (35) представляет собой падающую плоскую волну.

Из (35) следует выражение для ар [13]:

-^

f (0) =    S(21 + 1)al Pl (cos0).        (36)

² Ik l = 0

Коэффициенты a _l определяются из соотношения [13]:

a = -2 Ll h (ka)- ka//(ka)

^l      Lh ^{( 1 )}( ka ) - kah p) ( ka )

т ( dln X где L l =1

I dln r

— логарифмическая производ- ная на границе r = a; производные в (37) берутся по аргументу kr . Логарифмические производные Ll легко рассчитываются при помощи решений X, . Например, решением (34) при постоянном показателе преломления n(r) = n = с2/ c12 является функция

~- / x X Л nk\r T Z 7   , jl(k1r) = Aid ..J 1( k1r), V 2    l+2

c где k1 = k—; Al — некоторые постоянные коэф-c1

фициенты. При этом для нахождения величин L_l отпадает необходимость вычисления постоянных A_l , которые в этом случае просто сократятся.

Отметим, что имеет место соотношение [13]

al = (e2■ -1).

СЛУЧАЙ ОДНОРОДНОГО ШАРА

Наиболее простым для анализа является случай, когда в качестве объемного рассеивателя выбран шар B , радиусом a с центром в начале координат. Плотность шара совпадает с плотностью окружающей среды, скорость звука постоянна:

m ( x ) =

11 - c ²/ c ₁ ²| = M = const, x e B ;

0, x G B .

Рассмотрим ряд (36). Учитывая, что |P(x)| < 1, x e [-1,1], а также то, что при l >> 1 справедливо 21 +1 , отношение 2^—3 ~ 1, приходим к выводу, что скорость сходимости ряда (36) определяется поведением коэффициентов al. Для случая однородной сферы при различных радиусах a поведение коэффициентов al представлено в таблице. Скорость звука в окружающей среде с1 = 1500 м / с , частота f = 1000 Гц . Как видно, при a = 1м последовательность al мажорируется геометрической прогрессией со знаменателем 10–1 уже начиная с 10 = 5 ; при a = 2 м — начиная с 10 = 13 и т. д. Поэтому погрешность оценки ряда (36) конечной суммой 10 слагаемых (l = 0,1,...,10 -1), не превы-10

шает — a_l 0 . Реально с ростом a число слагаемых в конечной сумме ряда можно принимать значительно меньшим соответствующего значения l ₀ (см. таблицу).

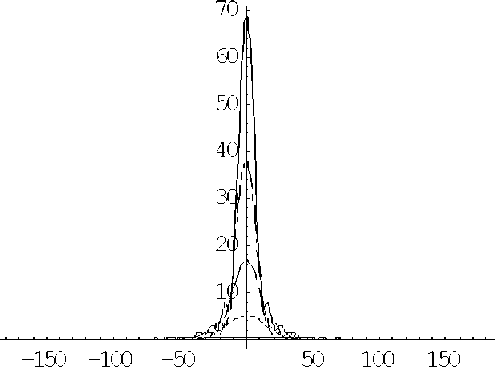
Ниже на рис. 6–10 представлены кривые модуля ар в зависимости от угла падения при a , равных соответственно 1м, 2м,…, 5м. На рис. 11 они представлены в одних координатах. Как видно, величина первого минимума кривых уменьшается от ~ ± 70 ° при a = 1 м до ~ ± 10 ° при a = 5 м. Амплитуда максимума при этом возрастает соответственно от 0.679 до 68.8.

Отметим, что близкие результаты получены автором при вычислении ар из системы одномерных интегральных уравнений (27) при n = 4 для случая, относящегося к рис. 6 ( f = 1000 Гц , a = 1, с = 1500м / с , с₁ = 1500м / с). Уравнения решались методом квадратур с использованием квадратурной формулы Симпсона [15]. Отметим, однако, что скорость вычислений при это уменьшилась практически на порядок по сравнению со случаем использования формул (36), (37).

Коэффициенты α _l в случае объемного рассеивателя в виде однородной сферы при различных радиусах a

l	a = 1 м	a = 2 м	a = 3 м	a = 4 м	a = 5 м
0	0.455	1	1.459	1.732	1.914
1	0.549	0.971	1.360	1.732	1.946
2	0.407	0.998	1.433	1.705	1.909
3	0.163	0.842	1.341	1.730	1.936
4	0.039	0.895	1.327	1.653	1.903
5	0.006	0.821	1.340	1.704	1.905
6	0.0006	0.533	1.172	1.620	1.903
13	1.1∙10–13	1∙10–5	0.047	1.07	1.595
14	2.28∙10–15	9.19∙10–7	0.012	0.723	1.571
20	1.2∙10–26	3.28∙10–14	1.52∙10–7	1.5∙10–3	0.249
21	1.1∙10–28	1.27∙10–15	1.48∙10–8	3.2∙10–4	0.109
27	1.2∙10–41	7∙10–25	1.62∙10–15	2.3∙10–9	3.7∙10–5
28	6.3∙10–44	1.5∙10–26	8.4∙10–17	2.3∙10–10	6.56∙10–6
35	1.9∙10–60	5.5∙10–39	1.2∙10–26	2.8∙10–18	3.5∙10–12
36	3.8∙10–63	212∙10–41	3.6∙10–22	1.6∙10–19	3.3∙10–13

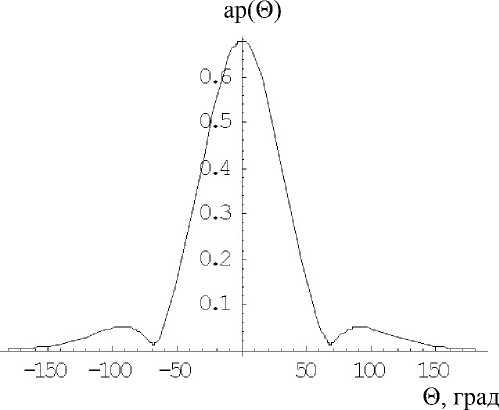
Рис. 6. Зависимость модуля ар от угла Θ при ka = 4/3 π , a = 1

ар(Θ)

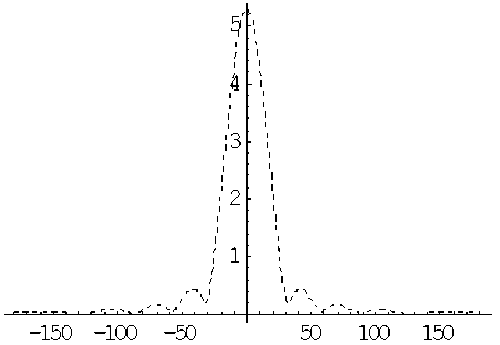
Θ, град

Рис. 7. Зависимость модуля ар от угла Θ при ka = 8/3 π , a = 2

ар(Θ)

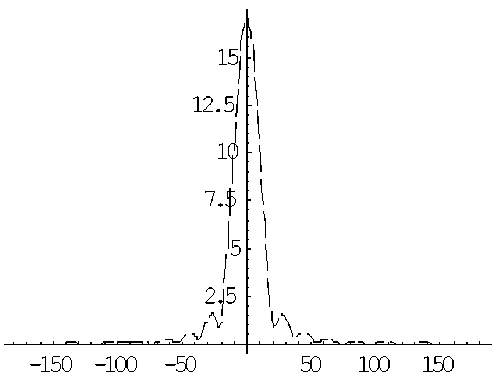
Θ, град

Рис. 8. Зависимость модуля ар от угла Θ при ka = 4 π , a = 3

ар(Θ)

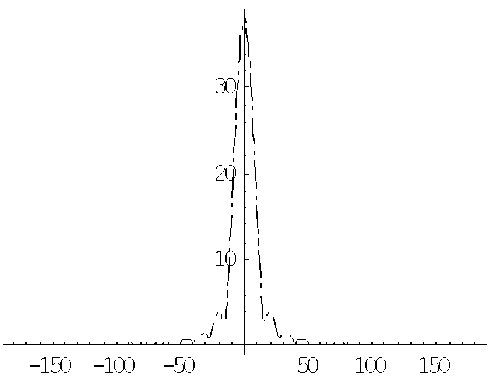
Θ, град

Рис. 9. Зависимость модуля ар от угла Θ при ka = 16/3 π , a = 4

ар(Θ)

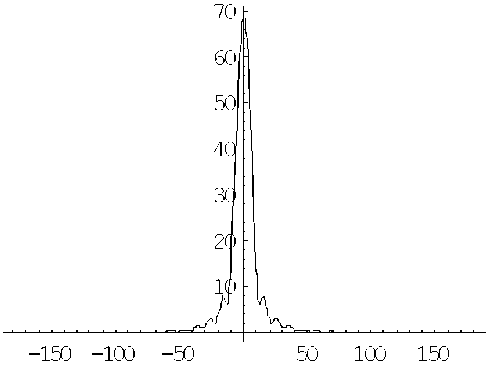
Θ, град

Рис. 10. Зависимость модуля ар от угла Θ при ka = 20/3 π , a = 5

ар(Θ)

Θ, град

Рис. 11. Зависимость модуля ар от угла Θ для всех случаев, показанных на рис. 6–10

АМПЛИТУДА РАССЕЯНИЯ ПОВЕРХНОСТНЫХ РАССЕИВАТЕЛЕЙ

Пусть в R3 в поле плоской падающей волны ui = eikix находится поверхностный рассеиватель, занимающий область D с гладкой замкнутой границей dD. Рассмотрим две задачи: на границе рассеивателя для суммарного поля падающей и рассеянной волн u (x) = ui + us выполняется

• 1)    однородное условие Дирихле

u ( x ) = 0, x ед D                (38)

или

• 2)    однородное условие Неймана

= 0, X ед D ,            (39)

dn где n — вектор внешней нормали к поверхности ∂D.

Тогда суммарное поле можно определить соответственно из выражений [12]:

u ( x ) = u_i ( x ) - ∫ ψ ( y ) G ( x - y )d s_y       (40)

∂D для условия Дирихле и

∂

u ( x ) = u_i ( x ) + ϕ ( y )     G ( x - y )d s_y

∂D     ∂n

для условия Неймана. В (40) и (41) x ∈ R ³ \ D ; n ^' в (41) — вектор внешней нормали к ∂ D в точке y ;

_(-)= 1 exp( ik I x - y I )

G ( x - y ) = ₄

4я x-y

.

Для определения функций ψ ( x ) и ϕ ( x ) из (40), (41) следуют интегральные уравнения [12]

¹ ψ ( x ) + ∫ ψ ( y ) ^∂ G ( x - y )d s_y =

• ²        ∂ D     ^{∂ n}

=^∂ u_i ( x ), x ∈∂ D ;

∂ n

1 ∂ ϕ ( x ) - ϕ ( y )    G ( x - y )d s_y =

• 2       ∂D      n

= u_i ( x ), x ∈∂ D .

Из (40), (41) следуют обычным порядком выражения для амплитуд рассеяния для обоих рассматриваемых случаев

T_D ( k _i , k _s ) =- ¹ ∫ ψ ( y )exp( - i k _s y )d s_y ,     (45)

4 π _{∂ D}

T_N ( k _i , k _s ) = ⁱ   ( k _s n ^') ϕ ( y )exp( - i k _s y )d s_y . (46)

4 π _{∂ D}

Здесь по-прежнему учтено, что имеют место зависимости

ψ ( x ) = ψ ( x , k _i ), ϕ ( x ) = ϕ ( x , k _i ).       (47)

В работе [12] приведено решение интегрального уравнения для шара с однородными условиями Дирихле и Неймана. В общем случае интегральные уравнения (43), (44) рассматриваются в работе [14].

плитуды рассеяния объемных и поверхностных рассеивателей, принятые в теории рассеяния волн и частиц. Приведены точные и приближенные методы вычислений. Указаны погрешности использования приближенных методов. Приведены примеры расчетов и некоторые вычислительные тонкости.